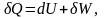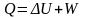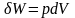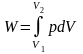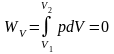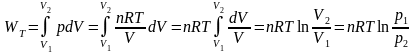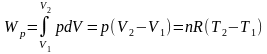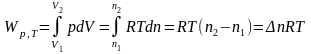1.1 Первое начало термодинамики

Первое начало термодинамики представ­ляет собой одну из формулировок закона сохранения энергии. Для бесконечно малого процесса его можно представить в виде

(1.2)

где Q – теплота процесса; U – внутренняя энергия системы; W – работа, совершаемая системой или над системой в термодинамическом процессе.

Понятия теплоты и работы применимы только к процес­сам, но не к состоянию системы. Теплота и работа являются функциями процесса, их изменение зависит от пути протекания процесса. Поэтому бесконечно малые величины теплоты и работы не обладают свойствами дифференциала и для их обозначения используют греческую букву δ. Внутренняя энергия, напротив, является функцией состоя­ния, поэтому для обозначения её бесконечно малого изменения используется знак дифференциала d.

Для конечного процесса первое начало термодинамики записывают:

(1.3)

Согласно первому началу термодинамики, теплота, подведенная к закрытой системе, расходуется на увеличение ее внутренней энергии и совершение работы.

В термодинамике используют следующую систему знаков. Положительной считают теплоту, подведенную к системе, а отрицательной – отведенную от нее. Работу, совершенную системой, считают положительной, а совершаемую над системой, например, работу сжатия – отрицательной.

Работа расширения идеального газа

Рассмотрим работу расширения газов, которое происходит во многих химико-технологических процессах. В общем случае работа расширении газа в бесконечно малом процессе равна

(1.4)

Для реального конечного процесса расширения газа

(1.5)

При не очень высоких давлениях (p < 10 атм) свойства газов близки к свойствам идеального газа. Поэтому для вычисления работы расширения будем использовать уравнение состояния идеального газа Менделеева-Клапейрона.

Работа расширения как функция процесса зависит от условий, в которых протекает процесс.

Изохорный процесс (V = const)

Если процесс протекает при постоянном объеме системы, то изменение объема dV = 0,

(1.6)

Изотермический процесс (T =const)

Из уравнения Менделеева-Клапейрона (1.1)

,

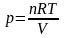тогда при T = const

(1.7)

Изобарный процесс (p = const)

(1.8)

Изобарно-изотермический процесс (p = const иT = const):

Из уравнения Менделеева-Клапейрона (1.1)

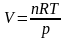
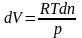
(1.9)

Таким образом, в изобарно-изотермических условиях работа расширения может совершаться только за счет изменения числа молей газа.

Теплота процесса в различных условиях

Изохорный процесс (V = const)

Работа изохорного процесса W = 0. Тогда, как следует из первого начала термодинамики, теплота процесса в изохорных условиях Q_V равна изменению внутренней энергии:

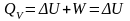
Так как внутренняя энергия является функцией состояния, то в изохорных условиях теплота

(1.10)

приобретает свойства функции состояния.

Изотермический процесс (T =const)

По закону Гей-Люсака-Джоуля внутренняя энергия идеального газа зависит только от температуры и не зависит от объема и давления. Следовательно, в изотермическом процессе не происходит изменения внутренней энергии (ΔU = 0). Тогда из первого начала термодинамики следует

(1.11)

Таким образом, вся теплота в изотермическом процессе идет на совершение работы, Работа изотермического процесса совершается за счет подведенной теплоты.

Изобарный процесс (p = const)

(1.12)

или для конечного процесса

(1.13)

Функция H = U + pV называется энтальпией.

Энтальпия, как и внутренняя энергия, является функцией состояния, поэтому в изобарных условиях теплота Q_Pприобретает свойства функции состояния.

Изохорный и изобарный тепловые эффекты связаны соотношением

(1.14)

Методы расчета и измерения тепловых эффектов химических реакций рассматриваются в разделе физической химии – термохимии. Рассмотрим практически важные из них.

Закон Гесса является основным законом термохимии. Он гласит:

Тепловой эффект процесса не зависит от пути его протекания (промежуточных стадий), а определяется начальным и конечным состоянием системы при условии, что давление и температура или объем системы и температура в ходе всего процесса остаются постоянными.

Закон Гесса позволяет рассчитывать тепловые эффекты реакций, если известны тепловые эффекты других реакций с участием тех же веществ. Из закона Гесса следует два важных следствия:

1. Тепловой эффект химической реакции равен разности сумм теплот образования продуктов реакции и исходных веществ (с учетом стехиометрических коэффициентов).

Теплотой образования вещества называется тепловой эффект реакции образования одного моля вещества из простых веществ. Простым веществом называется химическое соединение, состоящее из атомов одного элемента, в наиболее устойчивой модификации при данных условиях. В изобарных условиях теплота образования (энтальпия образования) обозначается Δ_fH (f – сокращение от английского слова formation – образование). Значения теплот образования при стандартных условиях 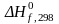для большого количества веществ приведены в таблицах стандартных термодинамических величин в справочниках (см., например, [2]). Стандартные условия – нормальное атмосферное давление 101325 Па (1 атм или 760 мм рт. ст.). Для термодинамических функций, стандартные условия указываются надстрочным индексом ^“0” . Например, H⁰.

2. Тепловой эффект химической реакции равен разности сумм теплот сгорания исходных веществ и продуктов реакции (с учетом стехиометрических коэффициентов).

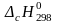Теплотой сгорания вещества Δ_cH (c – сокращение от английского слова combustion – горение) называется тепловой эффект реакции сгорания одного моля вещества в избытке кислорода до CO₂, H₂O_(ж.), N₂, SO₂ и галогеноводородов. Стандартные теплоты сгорания можно найти в справочниках, однако, они приведены для значительно меньшего количества веществ (в основном органических), чем теплоты образования.