3.1.3 Определение термодинамических параметров реакции, протекающей в гальваническом элементе

Для обратимо работающего гальванического элемента при Р и Т = const изменение энергии Гиббса 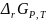равно максимальной полезной работе W, взятой с обратным знаком 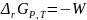. С другой стороны, электрическая работа, связанная с переносом заряда, соответствующего одному молю вещества, между электродами с разностью потенциалов Е (ЭДС), равна 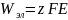(см. выражение (3.5)).

В результате получим выражение:

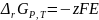(3.14)

Изменение энтропии, характеризующее электрохимическую реакцию, равно

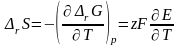(3.15)

Из термодинамики известно, что

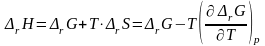(3.16)

Подставим в уравнение (3.16) уравнение (3.14), преобразуем и получим:

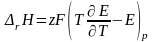(3.17)

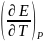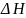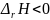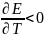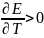Последнее уравнение является одной из форм уравнения Гиббса – Гельмгольца и позволяет рассчитать тепловой эффект реакции, протекающей в элементе, если известны его электродвижущая сила и температурный коэффициент ЭДС . Знак связан со знаком температурного коэффициента ЭДС. Действительно, (теплота выделяется), если или , но 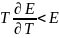. Энтальпия увеличивается (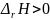 ), если и 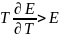. В последнем случае элемент работает с поглощением теплоты из окружающей среды. Если 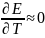, то 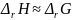, т.е. в этом случае все тепло практически можно превратить в работу, и коэффициент полезного действия такого элемента приближается к 100%.

При достижении равновесия при Т, Р = const изменение энергии Гиббса равно нулю и для термодинамической константы равновесия электро-химической реакции, протекающей в гальваническом элементе, справедливо:

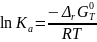, (3.18)

где 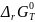– изменение энергии Гиббса химической реакции, протекающей при условии, что активности всех компонентов равны единице. По определению стандартный потенциал электрода – это потенциал при активностях окисленной и восстановленной формы равных единице. Стандартная ЭДС – разность стандартных потенциалов. Следовательно,

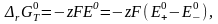(3.19)

где 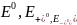– стандартная ЭДС и стандартные потенциалы положительного и отрицательного электродов, соответственно.

Пример: Составим элемент, в котором обратимо протекает реакция:

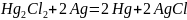
Используя стандартную ЭДС этого элемента рассчитаем стандартные термодинамические функции этой реакции, константу равновесия при температуре 325 К, если температурный коэффициент стандартной ЭДС составляет 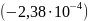В/К.

Решение: Сначала нужно выяснить, из каких электродов состоит гальванический элемент, на котором протекает данная реакция.

В данной реакции серебро окисляется, повышая свою степень окисления, а восстанавливается, понижая свою степень окисления. Хлорид серебра 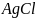и каломель , участвующие в реакции, являются малорастворимыми соединениями (см. таблицу 78 справочника [2]), следовательно, они входят в состав электродов второго рода: хлорсеребрянного и каломелевого.

Запишем электродные реакции, протекающие на электродах с учетом стехиометрических коэффициентов заданной реакции:

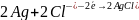
и

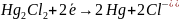
В суммарной реакции участвуют 2 электрона ( ).

Электрод, на котором протекает реакция окисления (хлорсеребрянный), будет располагаться на схеме гальванического элемента слева, а электрод, на котором идет реакция восстановления (каломелевый), - справа.

Электроды второго рода обязательно включают в себя хорошо растворимое соединение с анионом, одноименным аниону малорастворимого соединения. Поэтому хорошо растворимое соединение нужно включить в схему гальванического элемента, несмотря на то, что оно не входит в суммарную реакцию.

Гальванический элемент можно представить в виде гальванического элемента с переносом ионов через границу раздела жидких фаз (т.е., с двумя жидкими фазами, между которыми располагается мембрана или электролитический мостик):

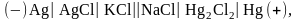
или без переноса ионов через границу раздела жидких фаз (с одной жидкой фазой, общей для двух электродов):

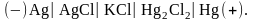
В таблице 79 [2] найдем стандартные потенциалы хлорсеребрянного и каломелевого электродов: +0,222 В и +0,268 В, соответственно. Стандартная ЭДС данного гальванического элемента при Т = 298 К:

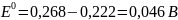
Используя температурный коэффициент ЭДС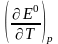 и приняв, что в указанном интервале температур зависимость Е⁰ = f(T) линейна, найдем:

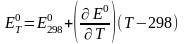
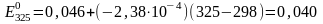В.

По формуле (3.19) найдем :

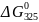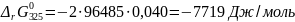
Термодинамическую константу равновесия найдем из формулы (3.18):

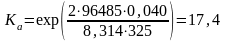
Далее по формулам (3.15) и (3.16) рассчитаем изменение энтропии и тепловой эффект реакции при 325 К:

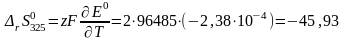Дж/(моль·К)

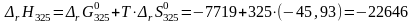Дж/моль.