Контрольная работа № 2 основы электродинамики. Магнитное поле. Электромагнитные явления. Электромагнитные волны. Примеры решения задач

Пример 1. Три точечных заряда Q₁ = Q₂ = Q ₃ = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q₄ нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?

Дано: Решение.

Q₁ = Q₂ = Q ₃ = 1 нКл Все три заряда, расположенные по вершинам

Q₄ - ? треугольника, находятся в одинаковых условиях.

Поэтому достаточно выяснить, какой заряд следует поместить в центре

треугольника, чтобы какой-нибудь один из трех зарядов, например Q₁, находился в равновесии. Заряд Q₁ будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рис. 2).

₂ + ₃ + ₄ = + ₄ = 0 (1)

г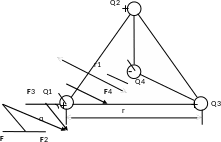 де ₂, ₃, ₄ – силы, с которыми

соответственно действуют на

заряд Q₁ заряды Q₂, Q₃, Q₄;

– равнодействующая сил

₂ и ₃.

Рис.2

Так как силы и ₄ направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным.

F – F₄ = 0, откуда F₄ = F.

Выразив в последнем равенстве F через F₂ и F₃ и учитывая, что F₃ = F₂, получим

.

Применив закон Кулона и имея в виду, что Q₁ = Q₂ = Q ₃ , найдем

, откуда

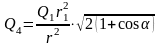. (2)

Из геометрических построений в равностороннем треугольнике следует, что

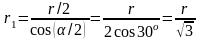, соs α = cos 60^o = 1/2.

С учетом этого формула (2) примет вид

Q₄ = Q₁ / .

Произведем вычисления.

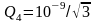= 5,77∙ 10 ^{– 10} Кл = 577 пКл.

Ответ: Q₄ = 577∙ 10 ^{– 12} Кл = 577 пКл

Пример 2. Два точечных электрических заряда Q ₁ = 1 нКл и Q ₂ = - 2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга.

Определить напряженность 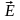и потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от заряда Q ₁ на расстояние r₁ = 9 см и от заряда Q ₂ на r₂ = 7 см.

Д ано: Решение.

Q ₁ = 1 нКл

Q ₂ = - 2 нКл

d = 10 см

r₁ = 9 см

r₂ = 7 см

Е = ? φ = ?

Рис.3

Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей ₁ и ₂ полей, создаваемых каждым зарядом в отдельности: = ₁ + ₂. Напряженность электрического поля, создаваемого в воздухе (ε = 1) зарядами Q ₁ и Q ₂ ,

, (1)

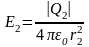. (2)

Вектор ₁ (рис. 9) направлен по силовой линии от заряда Q ₁ , так как этот заряд положителен; вектор ₂ направлен также по силовой линии, но к заряду Q ₂ , так как этот заряд отрицателен.

Модуль вектора найдем по формуле векторной алгебры.

Е = 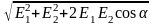, (3)

где α – угол между векторами ₁ и _2;

сos α может быть найден из треугольника со сторонами r₁ , r₂ и d по теореме косинусов (рис. 3)

; сos (π-α) = - cos α . Тогда

.

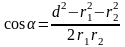Во избежание громоздких записей удобно значение cos α вычислить отдельно.

.

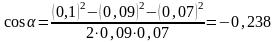Подставляя выражение Е₁ из (1) и Е₂ из (2) в (3) и вынося общий множитель 1/(4πε₀) за знак корня, получаем

. (4)

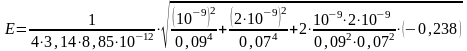= = 3,58 ∙ 10 ³ В/м = 3,58 кВ/м.

В соответствии с принципом суперпозиции электрических полей потенциал φ результирующего поля, создаваемого двумя зарядами Q ₁ и Q ₂ , равен алгебраической сумме потенциалов

φ = φ₁ + φ_2. (5)

Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой

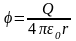. (6)

Согласно формулам (5) и (6) получим

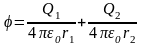, или

.

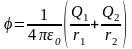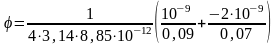= - 157 В.

Ответ: Е = 3,58 кВ/м; φ = - 157 В

Пример 3. На пластинах плоского конденсатора находится заряд Q = 20 нКл. Площадь S каждой пластины конденсатора равна 100 см ², диэлектрик – воздух. Определить силу F, с которой притягиваются пластины. Поле между пластинами считать однородным.

Дано: Решение.

Q = 20 нКл Заряд Q одной пластины находится в поле

S =100 см ² напряженностью Е, созданном зарядом другой пластины

F -? конденсатора. Следовательно, на первый заряд действует

сила

F = Q ∙Е. (1)

Так как

,

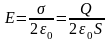где σ - поверхностная плотность заряда пластины, то формула (1) примет вид

.

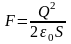Произведем вычисления.

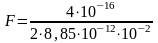= 22,6∙ 10 ^-4 Н

Ответ: F = 22,6∙ 10 ^-4 Н

Пример 4. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 10 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии a₁ = 0,5 см и a₂ = 2 см от поверхности цилиндра, в средней его части.

Дано: Решение.

R = 1 см Для определения разности потенциалов

τ=10 нКл/м воспользуемся соотношением между напряженностью

a ₁ = 0,5 см поля и изменением потенциала.

a ₂ = 2 см = - 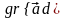φ;.

φ ₁ - φ ₂ = ? Для поля с осевой симметрией, каким является поле

цилиндра, это соотношение можно записать в виде

, или dφ = - E dr.

Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r ₁ и r ₂ от оси цилиндра

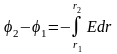. (1)

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром.

.

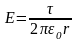Подставив выражение Е в (1), получим

,

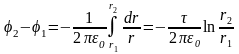или

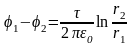. (2)

Произведем вычисления, учитывая, что величины r ₁ и r ₂ , входящие в формулу (2) в виде отношения, можно выразить в сантиметрах (r ₁ = R + a ₁ = 1,5 см , r ₂ = R + a ₂ = 3 см ) .

= 1∙ 10 ^{– 8} ∙1,8 ∙ 10 ¹⁰ ∙ ln (3/1,5) = 1,8 ∙ 10 ² ∙ 2,3 ln 2 = 125 В.

Ответ: = 125 В

Пример 5. Электрическое поле создается двумя зарядами Q₁ = 4 мкКл и Q₂ = - 2 мкКл , находящимися на расстоянии а = 0,1 м друг от друга. Определить работу А_{1, 2} сил поля по перемещению заряда Q = 100 нКл из точки 1 в точку 2 (рис. 4).

Дано: Решение.

Q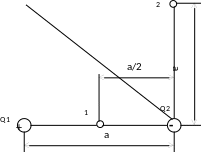 ₁ = 4 мкКл

Q₂ = - 2 мкКл

Q = 100 нКл

а = 0,1 м

А_{1, 2} - ?

Рис. 4

Для определения работы А_{1, 2} сил поля воспользуемся соотношением

А_{1, 2} =Q .

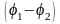Применяя принцип суперпозиции электрических полей, определим потенциалы φ ₁ и φ ₂ точек 1 и 2 поля

;

.

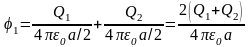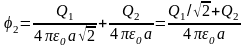Тогда

,

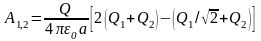или

.

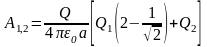Проверим, дает ли правая часть равенства единицу работы (Дж).

Подставим числовые значения физических величин в СИ (Q = 100∙10 ^{– 9} Кл , Q₁ = 4∙10 ^{– 6} Кл , Q ₂ = -2∙10 ^{– 6} Кл , а = 0,1 м , 1/(4πε₀)= 9 ∙ 10 ⁹ м/Ф ) и произведем вычисления.

=28,6 мДж

Ответ: А_{1, 2} = 28,6 мДж