Otchet_DM_Lab_4_2_semestr

Лабараторная работа №2

Илмурадов Максим ИНФ-12-1

Вариант 6

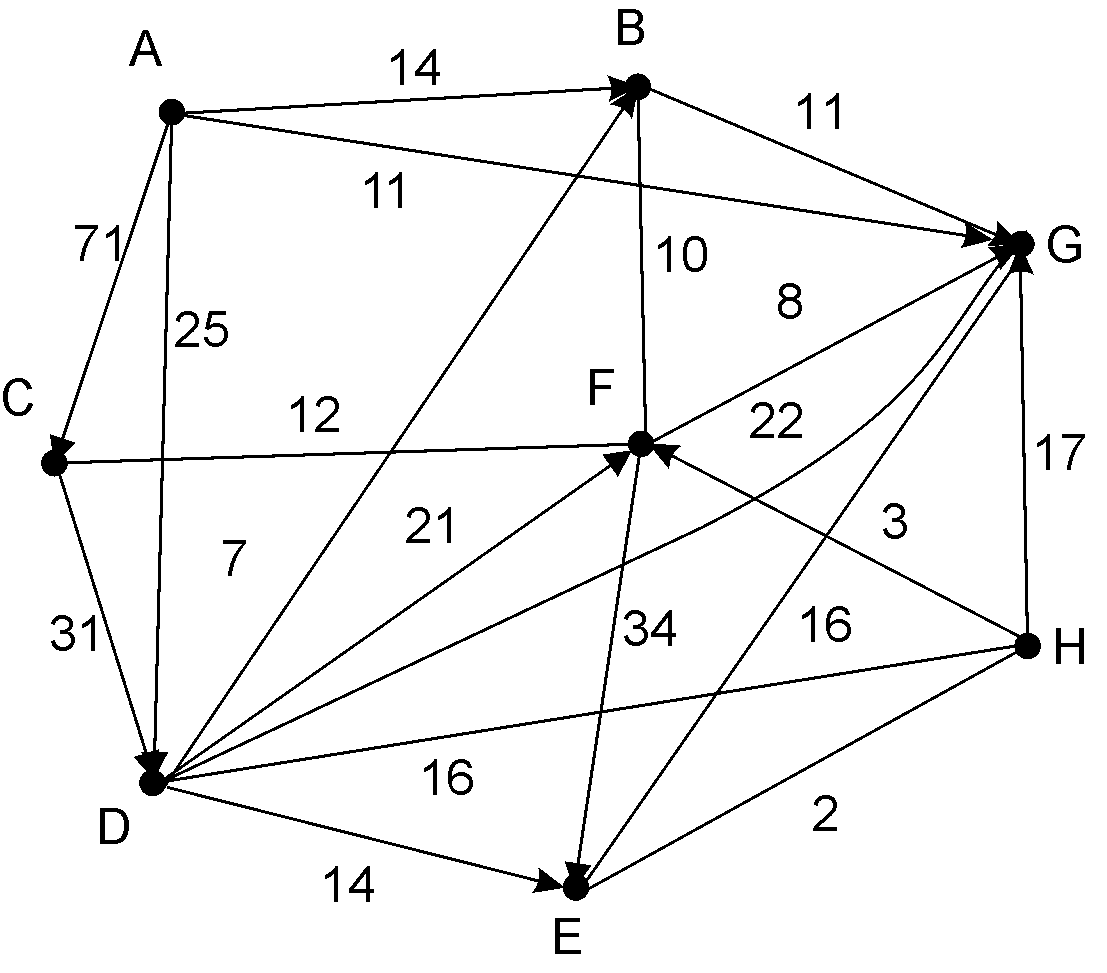
Написать программу, реализующую алгоритм Дейкстры, найти кратчайшие пути на графе от заданной вершины к остальным. Для реализации программы необходимо исходный граф представить в виде матрицы весов.

Вершина А

#include <iostream>

#include <limits.h>

#include <algorithm>

using namespace std;

#define N 8

#define INF INT_MAX

int input[N][N]=

{

{0, 14, 71, 25, 0, 0, 11, 0},

{0, 0, 0, 0, 0, 10, 11, 0,},

{0, 0, 0, 31, 0, 12, 0, 0},

{0, 7, 0, 0, 14, 21, 0, 16},

{0, 0, 0, 0, 0, 0, 16, 2},

{0, 10, 12,0, 34, 0, 8, 0},

{0, 0, 0, 0, 0, 0, 0, 0},

{0, 0, 0, 16, 2, 3, 17, 0}

};

int rost[N];

int start=0;

void dejkstra(int start, int* dist)

{

bool used[N];

for(int i=0; i< N; ++i)

used[i]=false;

for(int i=0; i< N; ++i)

rost[i]= INF;

rost[start]= 0;

int cur= start;

while(!used[cur])

{

used[cur]= true;

for(int i=0; i<N; ++i)

if(input[cur][i])

rost[i]= min(dist[i], input[cur][i]+dist[cur]);

int min= INT_MAX;

for(int i=0; i<N; ++i)

{

if(!used[i] && (rost[i] < min))

{

cur= i;

min= dist[i];

}

}//for

}//while

for(int i=0; i< N; ++i)

if(rost[i]==INF) rost[i]=-1;

}//dejkstra

int main()

{

setlocale(0,"");

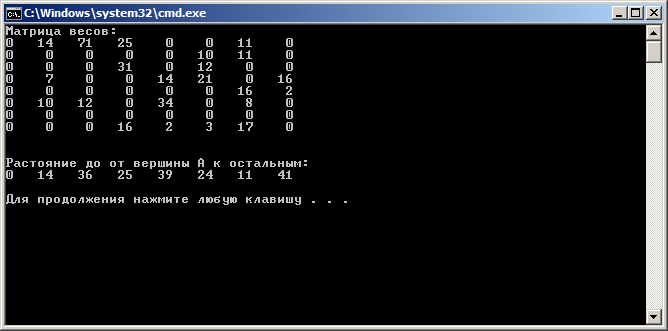
cout<<"Матрица весов:\n";

for(int i=0; i< N; ++i, cout<<'\n')

for(int j=0; j< N; ++j)

{

cout<<input[i][j];

cout.width(5);

}

cout<<"\n\n";

dejkstra(start, rost);

cout<<"Растояние до от вершины А к остальным: \n";

for(int j=0; j< N; ++j)

{

cout<<rost[j];

cout.width(5);

}

cout<<'\n';

cout<<'\n';

return 0;

}