Лабораторная работа № 2

Определение основных характеристик перелёта Автоматических Межпланетных Станций (АМС) к другим телам Солнечной системы.

Цель работы:

Научиться рассчитывать основные характеристики перелета АМС к какому-то телу Солнечной системы.

Оборудование:

Методическое руководство к выполнению данной работы (на компьютере), компьютер или калькулятор.

Отводимое время:

На выполнение работы отводится шесть учебных часов. Первые четыре часа – изучение теоретического материала и решение пробной задачи. Следующие два часа – выполнение контрольного задания, которое выдаст преподаватель. Те из студентов, которые справятся с работой быстрее, могут с разрешения преподавателя быть свободными. К концу четвёртого часа все сдают тетради для практических занятий для проверки результата, не зависимо от того, закончена работа или нет. При выполнении контрольного задания разрешено пользоваться своей тетрадью для практических занятий.

Требования к оформлению работы:

В тетради для самостоятельных и практических занятий по астрономии должен быть подробно представлен весь ход решения пробной и зачётной задач, включая черновые записи и исправления.

Результат работы:

Правильное решение контрольной задачи.

Точность расчетов:

При определении стартовой скорости ошибка не должна превышать100 м/с, длительности перелёта – 1 суток, углов – 1 градуса, расстояний – 0,1 астрономической единицы (а.е.)

Запрещается:

При проведении вычислений запрещается пользоваться готовыми программами. Все вычисления в режиме калькуляции.

Теория вопроса.

Точное решение задачи, связанной с движением тела пробной массы (АМС) в полях тяготения сразу нескольких тел (Земля, Солнце, Луна и т.д.) достаточно сложная задача. Строгого аналитического решения её до сих пор не получено и, скорее всего, невозможно вообще. Но с любой точностью она может быть решена методом численного интегрирования, что и делается в настоящее время в случае реальных запусков межпланетных станций.

Мы будем поступать проще – будем рассматривать движение АМС последовательно, сначала в поле притяжения Земли не учитывая притяжения Солнца, затем, мысленно отбросив Землю, в поле тяготения Солнца и, наконец, в поле тяготения планеты – цели полёта, где притяжением Солнца снова будем пренебрегать.

Не смотря на такой упрощенный подход к решению задачи, все характеристики перелётных траекторий оказываются достаточно близкими к характеристикам реальных перелетных траекторий. Кроме того, такой упрощенный подход помогает более чётко представить всю картину полета к другому телу солнечной системы.

Кроме того, мы сделаем ряд допущений, которые помогут существенно упростить решение задачи.

Во-первых, мы будем полагать, что плоскости орбит всех тел Солнечной системы совпадают с плоскостью орбиты Земли. На самом деле это конечно не так. Но у большинства тел системы углы между плоскостью их орбиты и плоскостью орбиты Земли (наклонения орбит – i ) не превосходят нескольких градусов. Исключения составляют только некоторые астероиды и кометы. Из крупных тел Солнечной системы значительным наклонением характеризуется орбита Плутона ( i = 13^о ). Такое упрощение позволит исключить из наших расчетов широтные маневры и значительно упростит решение, не особенно влияя на точность расчетов.

Во-вторых, мы будем полагать, что наш космодром ( К ) находится на экваторе Земли, а ось её вращения перпендикулярна плоскости её орбиты. Тем самым наш космодром и космический корабль сразу находится в плоскости всех планетных орбит (см. рис.1).

Рис. 1

Здесь:

С – Солнце;

Чёрные точки – планеты Солнечной системы (их размеры и их расстояния от Солнца условны).

К – космодром, с которого будет производиться запуск АМС.

Вы должны понимать, что полёт АМС в поле тяготения Солнца будет происходить только по эллиптическим орбитами и таким образом, что Солнце будет н аходиться в одном из фокусов перелётного эллипса. Из огромного

числа различных по форме и размерам

Рис. 2 возможных перелётных эллипсов,

пересекающих орбиты Земли и нужной нам планеты, мы будем рассматривать только полуэллиптические траектории перелёта. Их другое название – гомановские – им присвоено по имени немецкого учёного Гомана, который первым предложил осуществлять межпланетные перелёты по таким орбитам.

Первая особенность такой орбиты заключается в том, что перелетная траектория касается орбит планеты старта и планеты финиша в точках её перигелия и афелия. На рис. 2 показана полуэллиптическая траектория перелёта АМС от Земли (голубая точка) к какой-то внешней планете (красная точка). Солнце (С) находится в фокусе перелётного эллипса.

Таким образом, третье наше допущение сводится к тому, что наша перелётная траектория – полуэллипс. Здесь необходимо отметить, что и в действительности большая часть реальных полётов АМС происходит практически по полуэллиптическим орбитам. Тому есть важная особенность таких траекторий. Дело в том, что гомановская орбита является самой энергетически выгодной, хотя и требует самых длительных времён перелёта. Можно (см. рис. 3 ) долететь до нашей планеты гораздо быстрее, но для этого необходимо в точке старта АМС сообщить ей большую, чем в первом случае стартовую скорость. Это потребует дополнительного расхода топлива.

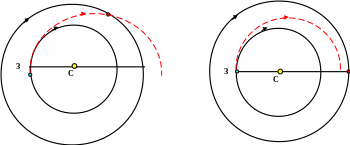
Рис. 3 Рис. 4

Если же при старте ракеты мы истратим топлива меньше, чем необходимо для полёта по полуэллипсу, то мы просто не долетим (см. рис 4) до нужной планеты. Говоря по-другому, кинетической энергии АМС будет недостаточно для того, чтобы подняться над поверхностью Солнца на такую высоту, где двигается наша планета.

Четвёртое наше допущение заключается в то, что мы будем считать орбиты всех планет круговыми. Это позволит нам избежать расчётов таких промежуточных величин как средняя, эксцентрическая и истинная аномалии. Такое допущение вполне оправдано, так как эксцентриситеты всех больших планет очень близки к нулю. Например, для орбиты Земли это 0,0167. На наших рисунках отличие эллипса с таким эксцентриситетом от окружности было бы в несколько раз меньше толщины линии, которой нарисована орбита Земли.

Но прежде чем приступать к разбору решения какой-либо задачи необходимо понять ещё несколько моментов.

Если мы будем стартовать с поверхности Земли, то стартовая скорость должна быть больше второй космической скорости – скорости освобождения для нулевой высоты, равной 11,19 км/сек. Если стартовая скорость будет меньше, то наш космический аппарат просто не выйдет из поля притяжения Земли, и будет вращаться вокруг её как очередной ИСЗ.

Гораздо более интересна ситуация, когда АМС при старте сообщили скорость, равную точно 11,19 км/сек. Это значит, что кинетической энергии станции хватит только на то, чтобы выйти из поля притяжения Земли, и, следовательно, её скорость относительно Земли (геоцентрическая скорость) после выхода, будет равна 0 км/сек.

Следовательно, скорость АМС относительно Солнца (гелиоцентрическая скорость) по величине и направлению будет равна скорости движения Земли по её орбите. Отсюда следует, что при таком старте наша АМС будет «летать» вокруг Солнца по орбите Земли, и никакого перелёта к другоё планете не получилось.

Вывод, к которому мы пришли, сводится к следующему: если мы хотим полететь к какому-либо телу Солнечной системы, наша стартовая скорость (при старте с поверхности Земли) должна быть больше второй космической скорости.

Определение основных характеристик полета по таким орбитам будет опираться на те же самые соотношения, с которыми мы работали при определении характеристик движения ИСЗ. Рассмотрим это на примере полета, например, на Марс.

Пробная задача.

Определить основные характеристики старта и полета АМС к Марту, если известно, что большая полуось его орбиты равна а_♂ = 1,52 а.е. (астрономической единицы).

При решении таких задач будем считать известными следующие величины:

а = 1 а.е. = 149,6 × 10⁹ м. – большая полуось орбиты Земли;

М_© = 2 × 10³⁰ кг. – масса Солнца;

V_1к = 7,91 км/сек - первая космическая скорость;

Рис. 5

V_2к = 11,19 км/сек. - вторая космическая скорость.

V = 30 км/сек. – скорость движения Земли по орбите;

V_экв. = 0,5 км/сек. _- линейная скорость точек экватора, обусловленная вращением Земли вокруг оси.

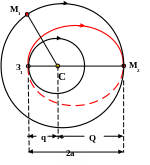
Решение задачи начинается с определения величины большой полуоси орбиты АМС.

Большая ось - 2а - перелётного эллипса (см. рис. 5) - это отрезок З₁ М₂ . Его величина равна сумме радиусов орбит Земли (СЗ₁) и Марса (СМ₂).

СЗ₁ = а = 1 а.е. ; СМ₂ = а_♂ = 1,52 а.е

2а = 1 а.е. +1,52 а.е = 2,52 а.е.

Следовательно, большая полуось перелётной орбиты АМС будет равняться половине - а = 1,26 а.е.

Из рисунка так же видно, что перигелийное расстояние равно радиусу Земной орбиты, а афелийное расстояние равно радиусу орбиты Марса:

q = 1 а.е. Q = 1,52 а.е.

Это позволяет сразу рассчитать эксцентриситет перелетной орбиты, используя любое из известных Вам соотношений:

q = a×(1-е); (1)

Q = а×(1+е); (2)

Эксцентриситет равняется:

е = (а – q)/а = (Q – а)/ а = 0,206

Следующий этап работы – это определение периода полного обращения АМС вокруг Солнца. Такое случится, если АМС не попадёт в Марс.

При выполнении лабораторной работы, посвященной определению основных характеристик движения ИСЗ (лабораторная работа №1) величину его периода обращения вокруг Земли мы определяли, опираясь на обобщенный третий закон Кеплера:

Т²/а³ = 4π²/GM = 4π²/ K

Поскольку АМС двигается в поле тяготения Солнца, то в этом случае в этом соотношении массу Земли (или её гравитационный параметр) необходимо заменить на соответствующие величины для Солнца:

Т²/а³ = 4π²/GM_© = 4π²/ K_©

Поскольку значение постоянной тяготения – G - мы знаем в СИ, значит в этом соотношении при определении Т – периода обращения АМС вокруг Солнца мы должны подставлять большую полуось – а – в метрах, массу Солнца - M_© - в килограммах. Величину периода обращения получим в секундах, которые последовательно будет необходимо перевести в минуты, часы, сутки и (возможно) годы.

Более рациональным в этом случае будет другой путь. Воспользуемся 3-им законом Кеплера в его классической формулировке:

«Квадраты периодов обращений тел солнечной системы вокруг Солнца относятся как кубы больших полуосей их орбит».

Т₁² / Т₂² = а₁³/а₂³ или:

Т₁² / а₁³ = Т₂²/а₂³ = const (3)

В астрономии при решении многих задач пользуются так называемой Гауссовой системой единиц. В такой системе единиц за единицу массы принимается масса Солнца, за единицу расстояния астрономическая единица – большая полуось орбиты Земли, за единицу времени - период обращения Земли вокруг Солнца – сидерический год. Если в качестве первой планеты взять Землю, то в этой системе единиц значение константы в уравнении 3 будет равно единице.

Можно сказать, что квадрат периода обращения какого-то тела Солнечной системы вокруг Солнца в годах будет численно равен кубу большой полуоси его орбиты в астрономических единицах:

Т²(год) = а³ (а.е.) (4)

Именно такие соображения позволяют наиболее простым способом определить период обращения АМС вокруг Солнца:

Т_АМС = ( а³ )^0,5 = (1,26 ³)^0,5 = 1,414 года.

Поскольку орбита перелета – полуэллипс, то перелётное время АМС от Земли до Марса будет равно полупериоду её обращения вокруг Солнца: ∆Т = 0,5 ×_. Т_АМС = 0,5 × 1,414 = 0,707 года

Л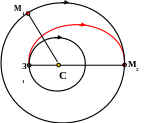 егко сообразить, что АМС «попадёт» в Марс только в том случае, если и АМС и Марс окажутся в точке м₂ одновременно. В противном случае АМС будет вращаться вокруг Солнца как искусственная планета солнечной системы.

Это значит, что АМС должна стартовать при строго определённом

взаимном положении Земли и Марса

Рис 6 на орбитах.

Вернёмся к рисунку (рис. 6). В момент старта АМС с Земли, Марс должен находиться в такой точке М₁ , чтобы отрезок своей орбиты М₁М₂ Марс прошёл за время полета АМС по полуэллипсу от Земли до Марса, то есть

за 0,707 года.

Определим величину дуги М₁М₂ в градусах.

Для этого сначала нужно рассчитать период обращения Марса вокруг Солнца. Будем исходить из классической формулировки третьего закона Кеплера (уравнение 4 ) :

Т_♂ = ( а³_♂ )^0,5 = (1.52 ³)^0,5 = 1,874 года.

З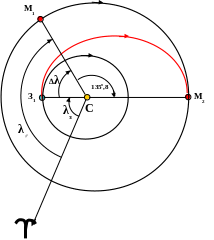 а такое время Марс проходит дугу 360 градусов. Тогда из элементарной пропорции найдём, какую дугу М₁М₂ Марс пройдёт за 0,707 года – время полёта АМС по перелётному эллипсу.

М₁М₂ = ( 360^о × 0,707 ) / 1,876 = 135^о,8

В действительности, зная дугу М₁М_2., рассчитывают величину ∆λ - разность гелиоцентрических долгот Марса и Земли.

Рис. 7

Напомню, что гелиоцентрические долготы - λ -отсчитываются от направления на точку весеннего равноденствия в направлении движения планеты до направления на неё. В нашем случае она равна:

∆λ = 180^о – 135^о,8 = 44^о,2