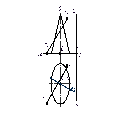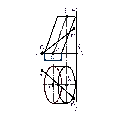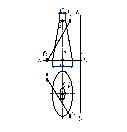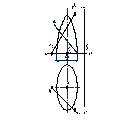Контрольные вопросы.

1. Как рассматриваются поверхности в начертательной геометрии?

2. Что такое определитель поверхности? Что такое очерк поверхности?

3. Сформулируйте условия принадлежности точки поверхности.

4. Приведите примеры кривых поверхностей.

5. Что такое поверхность вращения?

6. Какие точки линии пересечения относятся к характерным?

7. Как определить видимость проекций прямой?

8. Какое положение плоскости пересечения по отношению к поверхности является предпочтительным для определения линии пересечения?

Таблица. Исходные данные к лабораторной работе

	№ вар.	О			S			М				N
		x	y	z	x	y	z		x	y	z		x	y	z
	1	70	60	0	70	50	80		120	20	0		30	90	80
	2	70	60	0	70	50	80		110	50	80		20	30	0
	3	70	60	0	70	50	80		115	15	0		25	85	80
	4	70	60	0	70	50	80		115	45	80		25	25	5
		О			S			М				N
		x	y	z	x	y	z		x	y	z		x	y	z
	5	95	60	0	55	60	80		140	30	0		10	95	70
	6	40	50	0	95	50	80		120	0	0		40	90	80
	7	85	45	0	45	70	80		100	85	90		20	85	0
	8	95	65	0	45	45	80		95	95	80		30	10	0
		О			S			М				N
		x	y	z	x	y	z		x	y	z		x	y	z
	9	70	50	0	70	50	80		120	20	0		30	90	80
	10	70	50	0	70	50	80		110	50	80		20	30	0
	11	70	50	0	70	50	80		115	15	0		25	85	80
	12	70	50	0	70	50	80		115	45	80		25	25	5

				О							М							N
				x	y		z					x	y		z				x		y	z
	13			70	50		40					110	105		75				10		20	10
	14			70	50		40					125	55		10				40		85	85
	15			70	50		50					120	45		10				20		90	100
	16			70	50		45					110	95		85				35		25	10
			О							М								N
			x			y		z	x					y		z	x			y			z
		17	70			40		0	130					60		50	0			25			0
		18	70			40		0	140					10		15	15			65			55
		19	70			40		0	135					55		55	0			30			5
		20	70			40		0	130					40		30	20			75			85
			О							М								N
			x			y		z	x					y		z	x			y			z
		21	70			60		0	120					110		80	20			40			20
		22	70			60		0	110					60		30	20			95			55
		23	70			60		0	120					85		85	20			30			10
		24	70			60		0	120					15		80	20			85			55
			О							М								N
			x			y		z	x					y		z	x			y			z
		25	70			60		0	130					30		0	40			100			70
		26	70			60		0	130					0		50	20			65			80
		27	70			60		0	130					25		5	35			90			70
		28	70			60		0	120					85		85	20			10			30

Лабораторная работа № 5.

Позиционные задачи.

Цель - Закрепление знаний и приобретение навыков в решении позиционных задач на поверхностях общего вида.

Задание:

Пересечение 2-х поверхностей. Построить проекции линии пересечения двух поверхностей. Определить видимость линий.

Исходные данные выбираются по номеру варианта из приложения 1.

Задание выполнить на листе формата А3. Формат располагает вертикально. Основная надпись по ГОСТ 2.104-2006 форма 1.

Порядок выполнения работы

1. Дано: построить проекции линии пересечения поверхности тора Φ_Т с поверхностью сферы Φ_С: Φ_Т ∩ Φ_С = a.

Задача решается методом вспомогательных секущих плоскостей.

В качестве вспомогательных секущих плоскостей принимаются горизонтальные плоскости уровня Г_i|| П₁. Каждая из этих плоскостей пересечет обе поверхности по окружностям.

2. Построения начать с опорных точек (рис.1), не требующих дополнительных построений для их нахождения. К ним относятся точки А– высшая и В– низшая точки сечения, лежащие в плоскости Δ и принадлежащие главным меридианам тора и сферы на П₂ – А₂ и В_2. На плоскости проекций П₁ – точки А₁ и В₁ определяются с помощью линии связи. Эти точки устанавливают границы, в которых следует проводить вспомогательные плоскости.

Рисунок 1. Определение высшей и низшей точки линии пересечения.

Определяются точки С и С′ – точки пересечения экватора сферы с поверхностью тора. Для этого проведем плоскость Г, которая пересекает сферу по экватору m, тор – по параллели n. Окружности m и n, пересекаясь, определяют горизонтальные проекции точки С₁ и С′₁. Фронтальные проекции этих точек находятся на фронтальном следе секущей плоскости Г₂. Горизонтальные проекции точки С (С₁ и С′₁) разграничивают горизонтальную проекцию линии пересечения на видимую и невидимую части.

Г (Г₂) ∩ Φ_Т = n(n₂, n₁); Г (Г₂) ∩ Φ_С = m(m₂,m₁) ;

n (n₂,n₁) ∩ m(m₂,m₁) = С (С₁ и С′₁).

3. Промежуточные точки определяются с помощью плоскостей Г' Г'', которые пересекает сферу по окружностям m′ и m′', тор– по окружностям n′ и n′'. Пересекаясь, эти окружности дают точки, принадлежащие линии пересечения поверхностей (рис.3).

Г'(Г'₂) ∩ Φ_Т =n'(n'₂, n'₁); Г'(Г'₂) ∩ Φ_С= m'(m'₂, m'₁)

n'(n'₂,n'₁) ∩ m'(m'₂,m'₁) = D( D₁ D₂) и D′ (D′₁ D′₂)

Г''(Г''₂) ∩ Φ_Т =n''(n''₂, n''₁); Г''(Г''₂) ∩ Φ_С= m''(m''₂, m''₁)

n''(n''₂,n''₁) ∩ m''(m''₂,m''₁) = Е( Е₁ Е₂) и Е′ (Е′₁ Е′₂).

Количество секущих плоскостей зависит от требуемой точности построения.

Рисунок 2. Определение точек разграничивающих горизонтальную проекцию линии пересечения на видимую и невидимую части.

Рисунок 3. Определение промежуточных точек линии пересечения.

3. Полученные проекции точек соединяют плавной кривой с учетом видимости в той последовательности, в которой они располагаются на линии пересечения:

a= A∪D∪C∪…∪ A

a₁=A₁ ∪D₁∪C₁∪… ∪A₁

a₂=A₂ ∪D₂∪C₂∪… ∪A₂

Обвести видимые контуры пересекающихся поверхностей на проекциях сплошной основной линией, невидимые контуры поверхностей и невидимую часть линии их пересечения провести штриховой линией;

Рисунок 4. Решение задачи на взаимное пересечение двух поверхностей вращения.