
- •Электротехника и электроника
- •Общие методические указания
- •Указания к выполнению контрольных работ
- •Методические указания к решению задачи № 1
- •Методические указания к решению задач 2, 3,
- •Схемы к задаче 2
- •Схемы к задаче№ 3
- •Методические указания к решению задач 4 - 6
- •Схемы к задаче №6
- •Перечень рекомендуемых учебных изданий, Интернет – ресурсов, дополнительной литературы
Методические указания к решению задач 2, 3,
Эти задачи предусматривают расчёт однофазных неразветвленных и разветвленных цепей переменного тока. Перед их решением изучите материал тем 1.4, 1.5, ознакомьтесь с методикой построения векторных диаграмм и рассмотрите типовые примеры 2, 3, 4.
Пример
2.
Активное сопротивление катушки Rk=6Ом,
индуктивное
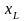 =10
Ом.
Последовательно с катушкой включено
активное сопротивление
=10
Ом.
Последовательно с катушкой включено
активное сопротивление
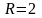 Ом
и конденсатор сопротивлением
Ом
и конденсатор сопротивлением
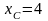 Ом
(рис. 2, а).
К цепи приложено напряжение U=50В
(действующее значение). Определить:1)
полное сопротивление цепи Z; 2) токI; 3)
коэффициент мощностиcosφ; 4) активнуюP,
реактивную Qи полную мощности S; 5)
напряжения на каждом сопротивлении.
Начертите в масштабе векторную диаграмму
цепи.
Ом
(рис. 2, а).
К цепи приложено напряжение U=50В
(действующее значение). Определить:1)
полное сопротивление цепи Z; 2) токI; 3)
коэффициент мощностиcosφ; 4) активнуюP,
реактивную Qи полную мощности S; 5)
напряжения на каждом сопротивлении.
Начертите в масштабе векторную диаграмму
цепи.
Решение. 1. Определяем полное сопротивление цепи:
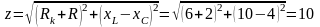 Ом
Ом
2. Определяем ток:
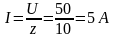
3. Определяем коэффициент мощности цепи:
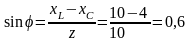 ;
;
по
таблице Брадиса находим
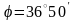 .
Угол сдвига фаз
.
Угол сдвига фаз находим по синусу во избежание потери
знака угла (косинус является четной
функцией).
находим по синусу во избежание потери
знака угла (косинус является четной
функцией).

4.Определяем активную мощность цепи:
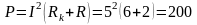 ВT
ВT
или
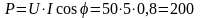 ВT
ВT
Здесь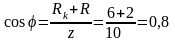
5. Определяем реактивную мощность цепи:
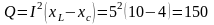 вар
вар
или
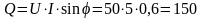 вар
вар
6. Определяем полную мощность цепи:
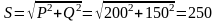 В·А
В·А
или
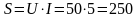 В·А
В·А
7. Определяем падения напряжения на сопротивлениях цепи:
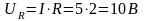 ;
;
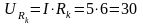 В;
В;
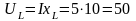 В;
В;
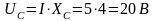
Построение
векторной диаграммы начинаем с выбора
масштаба для тока и напряжения. Задаемся
масштабом по току: в 1 см - 10 В. Построение
векторной диаграммы (рис. 2, б) начинаем
с вектора тока, который откладываем
погоризонтали в масштабе
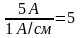 см.
см.
Вдоль
вектора тока откладываем, векторы
падений напряжения на активных
сопротивлениях
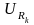 и
и
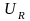 :
:
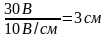 ;
;
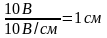
Из
конца вектора
откладываем в сторону опережения вектора
тока на 90° вектор падения напряжения
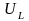 на индуктивном сопротивлениидлиной
на индуктивном сопротивлениидлиной
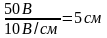 .
Из конца вектора
откладываем в сторону отставания от
вектора тока на 90º вектор падения
напряжения на конденсаторе
.
Из конца вектора
откладываем в сторону отставания от
вектора тока на 90º вектор падения
напряжения на конденсаторе
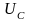 длиной
длиной
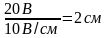 .
Геометрическая сумма векторов
,
,
и
равна
полному напряжению
.
Геометрическая сумма векторов
,
,
и
равна
полному напряжению
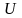 ,
приложенному к цепи.
,
приложенному к цепи.
Пример 3. На рис. 3, а задана векторная диаграмма для неразветвленной цепи, ток I и падения напряжений на каждом сопротивлении (U1,U2 и т. д.).

Определить характер и величину каждого сопротивления, начертить эквивалентную схему цепи, вычислить приложенное напряжение и угол сдвига фаз .
Решение. 1. Из векторной диаграммы следует, что напряжение U1отстает от тока на угол 90°. Следовательно, на первом участке включен конденсатор, сопротивление которого
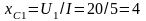 Ом
Ом
Вектор напряжения на втором участке U2 направлен параллельно вектору тока,
т. е. совпадает с ним по фазе. Значит, на втором участке включено активное сопротивление
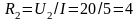 Ом
Ом
Вектор напряжения на третьем участке U3 опережает вектор тока на угол 90°, что характерно для индуктивности, сопротивление которой
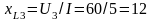 Ом
Ом
На четвертом участке включено активное сопротивление
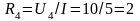 Ом
Ом
Эквивалентная схема цепи приведена на рис. 3, б.
2.Извекторной диаграммы определяем, значение приложенного напряжения и угол сдвига фаз:
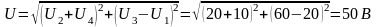
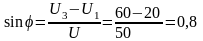 ;
;

Пример 4.Катушка с активным сопротивлением R1=6 Ом и индуктивнымxL1=8 Ом соединена параллельно с конденсатором, емкостное сопротивление которого xC2= 10Ом (рис. 4, а). Определить: 1) токи в ветвях I1 иI2 и дв неразветвленной части цепиI; 2) активныеPи Qреактивные мощности ветвей и всей цепиS; 3) полную мощность цепи; 4) углысдвига, фаз между током и напряжением в каждой ветви и во всей цепи. Начертить в масштабе векторную диаграмму цепи. К цепи приложено напряжение U=100 В.

Решение.1. Определяем токи в ветвях:
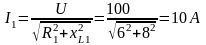
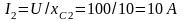
2. Углы сдвига фаз в ветвях находим по синусам углов во избежание потери знака угла:
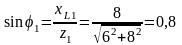 ;
;
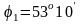
Так
как
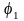 >0,
то напряжение опережает ток,
>0,
то напряжение опережает ток,
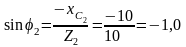 ;
;
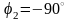 т.
е. напряжение отстает от тока, так как
т.
е. напряжение отстает от тока, так как
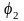 <0,
По таблицeБрадиса находим
<0,
По таблицeБрадиса находим
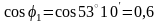 ;
;
 .
.
3. Определяем активные и реактивные составляющие токов в ветвях:
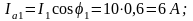
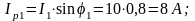
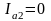 ;
;
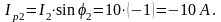
4. Определяем ток в неразветвленной части цепи:
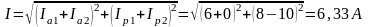
5. Определяем коэффициент мощности всей цепи:
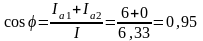
6. Определяем активные и реактивные мощности ветвей и всей цепи:
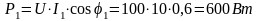 ;
;
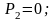
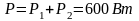 ;
;
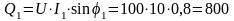 вар;
вар;
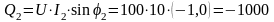 вар;
вар;
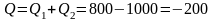 вар.
вар.
Внимание!
Реактивная мощность ветви с емкостью
отрицательная, так как
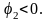
7. Определяем полную мощность цепи:
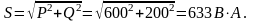
Ток в неразветвленной части цепи можно определить Значительно проще, без разложения токов на составляющие, зная полную мощность цепи и напряжение:
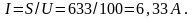
8. Для построения векторной диаграммы задаемся масштабом по току: в 1 см - 2,5 А и масштабом по напряжению: в 1 см - 25 В.
Построение
начинаем с вектора напряжения
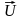 ,
который откладываем горизонтально
(рис. 4, б). Под углом
к нему (в сторону отставания) откладываем
в масштабе вектор тока
,
который откладываем горизонтально
(рис. 4, б). Под углом
к нему (в сторону отставания) откладываем
в масштабе вектор тока
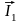 ,
под углом
(в сторону опережения) - вектор тока
,
под углом
(в сторону опережения) - вектор тока
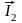 .
Геометрическая сумма этих токов равна
току в неразветвленной части цепи
.
Геометрическая сумма этих токов равна
току в неразветвленной части цепи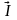 .
На диаграмме показаны также проекции
векторов токов на вектор напряжения
(активная составляющая
.
На диаграмме показаны также проекции
векторов токов на вектор напряжения
(активная составляющая
 )
и вектор, перпендикулярный ему (реактивные
составляющие
)
и вектор, перпендикулярный ему (реактивные
составляющие
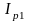 ,
и
,
и
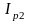 ).
).
Задача № 2 (варианты с 1 по 30)
Цепь переменного тока содержит различные элементы (резисторы, индуктивности, емкости), включенные последовательно. Схема цепи приведена на соответствующем рисунке. Номер рисунка и значения сопротивлений всех элементов, а также один дополнительный параметр заданы в табл. 4
Начертить схему цепи и определить следующие величины, относящиеся к данной цепи, если они не заданы в табл. 3:1) полное сопротивление z; 2) напряжение U, приложенное к цепи; 3) ток I; 4) угол сдвига фаз φ(по величине и знаку); 5) активную Р, реактивную Qи полную Sмощности цепи. Начертить в масштабе векторную диаграмму цепи и пояснить ее построение. С помощью логических рассуждений, пояснить характер изменения (увеличится, уменьшится, останется без изменения) тока, активной, реактивной мощности в цепи при увеличении частоты тока в два раза. Напряжение, приложенное к цепи, считать неизменным.
Указание. См. решение типового примера 3.
Примечание. В табл.4 индексы буквенных обозначений следует понимать так: QLl - реактивная мощность в первом индуктивном сопротивлении; QC1-то же, но в ёмкостном сопротивлении; PR1 - активная мощность в первом активном сопротивлении; UR1, UL1, Uc1 - падения напряжения соответственно в первом активном, индуктивном, первом ёмкостном сопротивлениях.
Таблица 4
Номер |
Номер |
R1 |
R2 |
ХL1 |
XL2 |
XC1 |
XC2 |
Дополнительный |
варианта |
рисунка |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
параметр |
1 |
16 |
4 |
- |
6 |
- |
3 |
- |
QL1 = 150 вар
|
2 |
17 |
6 |
2 |
3 |
- |
9 |
- |
U = 40 B
|
3 |
18 |
10 |
6 |
- |
- |
12 |
- |
I = 5 А |
4 |
19 |
6 |
2 |
6 |
- |
- |
- |
РR1 =150 Вт |
5 |
20 |
4 |
4 |
3 |
3 |
- |
- |
S = 360 В·А |
6 |
21 |
3 |
- |
- |
- |
2 |
2 |
I = 4 А |
7 |
22 |
8 |
- |
12 |
- |
4 |
2 |
Р = 200 Вт |
8 |
23 |
16 |
- |
10 |
8 |
6 |
- |
U = 80 B |
9 |
24 |
10 |
6 |
- |
- |
8 |
4 |
I = 2 А |
10 |
25 |
2 |
2 |
5 |
- |
6 |
2 |
Q = -192 вар |
11 |
16 |
3 |
- |
2 |
- |
6 |
- |
U = 50 B |
12 |
17 |
4 |
4 |
4 |
- |
10 |
- |
I = 4 А |
13 |
18 |
4 |
2 |
- |
- |
8 |
- |
URl = 20 B |
14 |
19 |
8 |
4 |
16 |
- |
- |
- |
S = 320 B·A |
15 |
20 |
6 |
10 |
8 |
4 |
- |
- |
Р = 400 Вт
|
16 |
21 |
6 |
- |
- |
- |
5 |
3 |
S = 160 В·А
|
17 |
22 |
12 |
- |
4 |
- |
12 |
8 |
I = 4 А |
18 |
23 |
6 |
- |
8 |
4 |
4 |
- |
Р = 54 Вт |
19 |
24 |
8 |
4 |
- |
- |
6 |
10 |
S = 180 В·А |
20 |
25 |
8 |
8 |
12 |
- |
4 |
2 |
Р = 256 Вт
|
21 |
16 |
6 |
- |
10 |
- |
2 |
- |
I = 5 А |
22 |
17 |
4 |
2 |
12 |
- |
4 |
- |
Р = 24 Вт |
23 |
18 |
5 |
3 |
- |
- |
6 |
- |
S = 250 В·А |
24 |
19 |
3 |
1 |
3 |
- |
- |
- |
QL1 = 80 вар
|
25 |
20 |
4 |
8 |
10 |
6 |
- |
- |
Q = 64 вар |
26 |
21 |
8 |
- |
- |
- |
4 |
2 |
U = 40 B |
27 |
22 |
6 |
- |
12 |
- |
2 |
2 |
ULl = 60 B |
28 |
23 |
4 |
- |
8 |
4 |
9 |
- |
Q = 75 вар |
29 |
24 |
2 |
6 |
- |
- |
4 |
2 |
UR2 = 24 B |
30 |
25 |
4 |
2 |
4 |
- |
8 |
4 |
QL1 = 16 вар
|
