Лабораторная работа № 4 промахи и методы их исключения

Цель работы: Определить наличие грубой погрешности и исключить подозрительные результаты.

Общие сведения

При проведении любых измерений часто возникаю дополнительные факторы, которые оказывают негативное влияние на точность полученных результатов. Результаты, резко отличающиеся от остальных, определяются как грубая погрешность (промах). Если отсчет отличается от основного массива информации на небольшое значение, то он определяется как предполагаемый промах.

Источником возникновения грубой погрешности могут служить : неправильный отсчет по шкале, неправильная запись результата измерений, хаотичное изменение параметров окружающей среды и параметров питающего напряжения, работа неквалифицированного персонала и другие факторы.

Исключить подобное влияние можно двумя способами. Если дальнейшую обработку ведет сам оператор, то он может воспользоваться своими воспоминаниями о нарушениях при проведении эксперимента, если проводится аппаратный анализ полученной информации или обработка другим оператором, то используются формальные методы анализа.

При однократных измерениях определить наличие грубой погрешности невозможно. Для этого необходимо провести несколько измерений и принять за результат среднее значение. Для обработки больших массивов информации необходимо применять формальные методы анализа, к которым относятся критерий 3σ, критерий Шарлье и т.д.

Критерий 3σ

Применяется для распределенных по нормальному закону результатов и при количестве измерений от 20 до 50. Критерий является следствием правила 3σ: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного значения среднеквадратического отклонения, в противном случае она является грубой погрешностью. Основное условие критерия: результат, возникающий с вероятностью q≤0.003, считается маловероятным и его можно считать промахом если

, (1)

где - среднее значение исследуемого ряда, вычисляется без учета экстремальных значений;

- экстремальное значение исследуемого ряда;

σ - среднеквадратическое отклонение измерения, вычисляется без учета экстремальных значений.

Так как критерий 3σ накладывает слишком жесткие ограничения, то в зависимости от объема выборки выбираются следующие границы цензурирования

при числе опытов 6<n<100 = 4σ;

при числе опытов 100<n<1000 = 4.5σ;

при числе опытов 1000<n<10000 = 5σ и т.д.

Пример

Для приведенного массива данных оцените вероятность появления грубого промаха в соответствии с критерием 3σ.

Таблица 1 - Результаты измерения листов сердечника электротехнической стали

n	1	2	3	4	5	6	7	8	9	10
Х, мм	0,25	0,19	0,26	0,27	0,25	0,25	0,24	0,23	0,27	0,26
n	11	12	13	14	15	16	17	18	19	20
Х, мм	0,24	0,25	0,23	0,26	0,27	0,24	0,23	0,25	0,23	0,26
n	21	22	23	24	25	26	27	28	29	30
Х, мм	0,26	0,25	0,28	0,24	0,23	0,25	0,26	0,24	0,22	0,22

Определим среднее значение ряда распределения без учета подозрительных значений.

Подозрительными значениями следует считать минимальное и максимальное значение полученного вариационного ряда для примера это 0,19 и 0,28

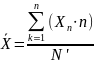, (2)

где N’ – количество измерений без учета подозрительных результатов.

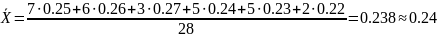мм

Определим среднеквадратическое отклонение без учета подозрительных результатов.
1. Определим абсолютную погрешность результата измерения и занесем полученные результаты в таблицу 2

. ⁽³⁾