Пределы и непрерывность Множества

Под множеством понимается совокупность однородных объектов. Объекты, которые образуют множество, называются элементами или точками этого множества. Множества обозначают прописными буквами, а их элементы – строчными. Если a является элементом множества A, то используется запись aA. Если b не является элементом множества A, то это записывается так: bA. Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается так: Ø.

Е сли множество B состоит из части элементов множества A или совпадает с ним, то множество B называют подмножеством множества и обозначают BA.

Д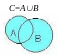 ва множества называют равными, если они состоят из одних и тех же элементов.

Объединением двух множеств A и B называется множество C, состоящее из всех элементов, принадлежащих хотя бы одному из множеств: C=AB.

П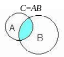 ересечением двух множеств A и B называется множество C, состоящее из всех элементов, принадлежащих каждому из данных множеств: C=AB.

Р азностью множеств A и B называется множество E, состоящее из всех элементов множества A, которые не принадлежат множеству B: .

Дополнением множества AB называется множество C, состоящее из всех элементов множества B, не принадлежащих A.

Множества, элементами которых являются действительные числа, называются числовыми:

R – множество действительных чисел; Q – множество рациональных чисел; I – множество иррациональных чисел;

Z – множество целых чисел; N – множество натуральных чисел.

При этом NZQR, IR и R=IQ.

Множество X, элементы которого удовлетворяют неравенству называется отрезком (сегментом) и обозначается [a; b]; неравенству a<x<b – интервалом и обозначается () ; неравенствам и - полуинтервалами и обозначаются соответственно и . Также часто приходится иметь дело с бесконечными интервалами и полуинтервалами: , , , и . Все их удобно называть промежутками .

Интервал , т.е. множество точек удовлетворяющих неравенству (где ), называется -окрестностью точки a.

Понятие функции. Основные свойства функции

Если каждому элементу x множества X ставится в соответствие единственный элемент y множества Y, то говорят, что на множестве X задана функция y=f(x). При этом x называют независимой переменной или аргументом, а y – зависимой переменной или функцией, а f обозначает закон соответствия. Множество X называют областью определения функции, а множество Y – областью значений функции.

Существует несколько способов задания функций.

1) Аналитический способ – функция задается формулой вида y=f(x).

2) Табличный способ – функция задается таблицей, содержащей значения аргумента и соответствующие им значения функции y=f(x).

3) Графический способ – изображение графика функции, т.е. множества точек (x; y) координатной плоскости, абсциссы которых представляют значения аргумента , а ординаты – соответствующие им значения функции y=f(x).

4) Словесный способ – функция описывается правилом ее составления. Например, функция Дирихле принимает значение 1, если x – рациональное число и 0, если x – иррациональное число.

Выделяют следующие основные свойства функций.

1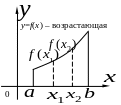 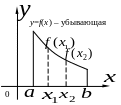Четность и нечетность Функция y=f(x) называется четной, если для любых значений x из области ее определения выполняется f(–x)=f(x), и нечетной, если f(–x)=–f(x). Если не выполняется ни одно из перечисленных равенств, то y=f(x) называется функцией общего вида. График четной функции симметричен относительно оси Oy, а график нечетной функции симметричен относительно начала координат.

2 Монотонность Функция y=f(x) называется возрастающей (убывающей) на промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Пусть x₁,x₂X, x₂>x₁. Тогда функция возрастает на промежутке X, если f(x₂)>f(x₁), и убывает, если f(x₂)<f(x₁).

Наряду с возрастающими и убывающими функциями рассматривают неубывающие и невозрастающие функции. Функция называется неубывающей (невозрастающей), если при x₁,x₂X, x₂>x₁ выполняется неравенство f(x₂)≥f(x₁) (f(x₂)≤f(x₁)).

Возрастающие и убывающие функции, а также невозрастающие и неубывающие функции называют монотонными.

3 Ограниченность Функция y=f(x) называется ограниченной на промежутке X, если существует такое положительное число M>0, что |f(x)|≤M для любого xX. В противном случае функция называется неограниченной на X.

4 Периодичность Функция y=f(x) называется периодической с периодом T≠0, если для любых x из области определения функции f(x+T)=f(x). В дальнейшем под периодом будем понимать наименьший положительный период функции.

Функция называется явной, если она задана формулой вида y=f(x). Если функция задана уравнением F(x, y)=0, не разрешенным относительно зависимой переменной y, то ее называют неявной.

Пусть y=f(x) есть функция от независимой переменной , определенная на множестве X с областью значений Y. Поставим в соответствие каждому yY единственное значение xX, при котором f(x)=y.Тогда полученная функция x=φ(y), определенная на множестве Y с областью значений X, называется обратной и обозначается y=f^–1(x). Графики взаимно обратных функций симметричны относительно биссектрисы первой и третьей координатных четвертей .

Пусть функция y=f(u) есть функция переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь является функцией u=φ(x), определенной на множестве X с областью значений U. Тогда заданная на множестве X функция y=f(φ(x)) называется сложной функцией (композицией функций, суперпозицией функций, функцией от функции).