
- •Контрольная работа №7
- •Контрольная работа №8
- •Контрольная работа № 9
- •Сделать чертеж.
- •Контрольная работа № 10
- •6. , ;
- •9. , ;
- •10. , .
- •Контрольная работа № 11
- •Контрольная работа №12
- •Вопросы программы второго курса Неопределенный интеграл
- •Определенный интеграл
- •Обыкновенные дифференциальные уравнения
- •Числовые ряды
- •Элементы операционного исчисления
- •Элементы уравнений математической физики
- •Элементы теории вероятностей и математической статистики
- •Литература
Сделать чертеж.
Задание №7. Проверить, является ли векторное поле F=Xi+Yj+Zk потенциальным и соленоидальным. В случае потенциальности поля F найти его потенциал.
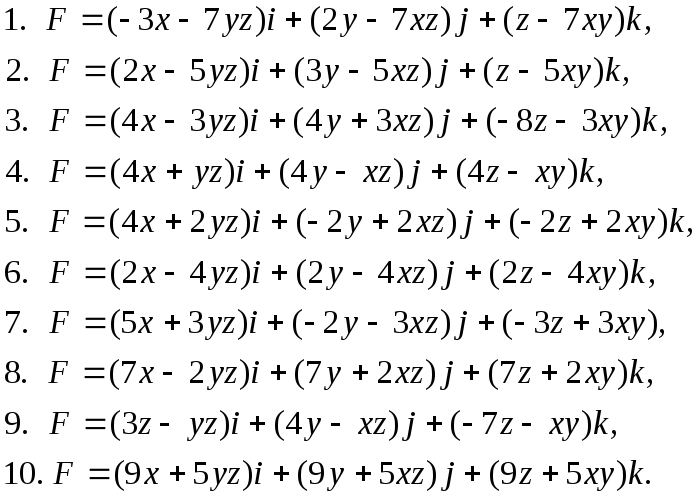
Контрольная работа № 10
Задание
№ 1.
Найти
аналитическую функцию ![]() по следующим условиям:
по следующим условиям:
1.
![]() ,
,
![]() ;
;
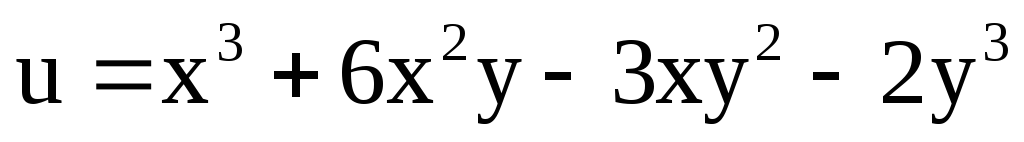 ,
,
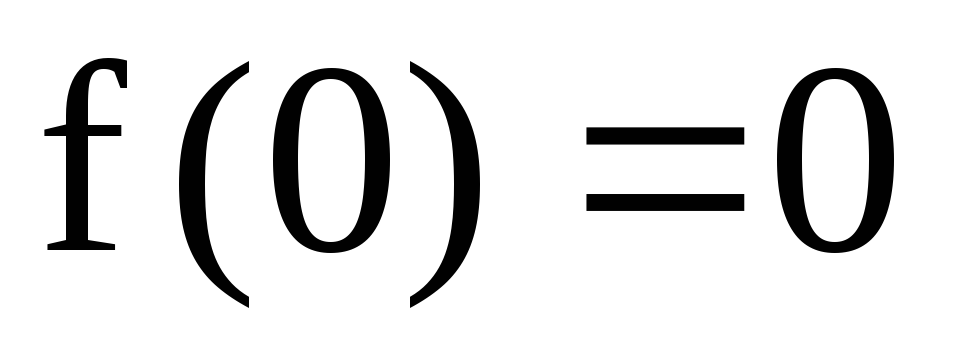 ;
;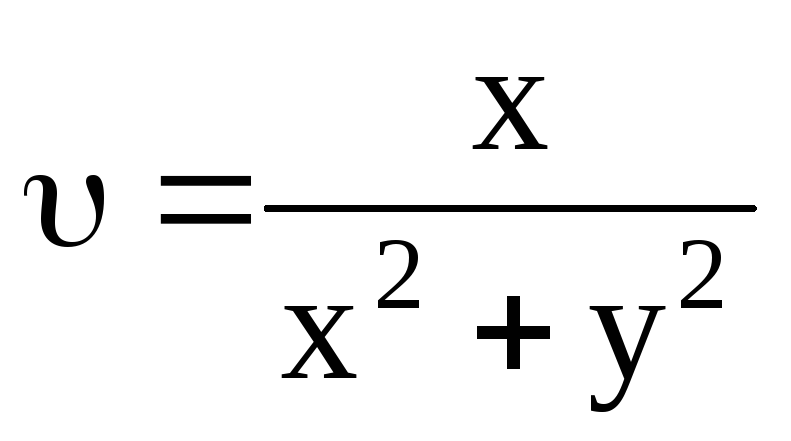 ,
,
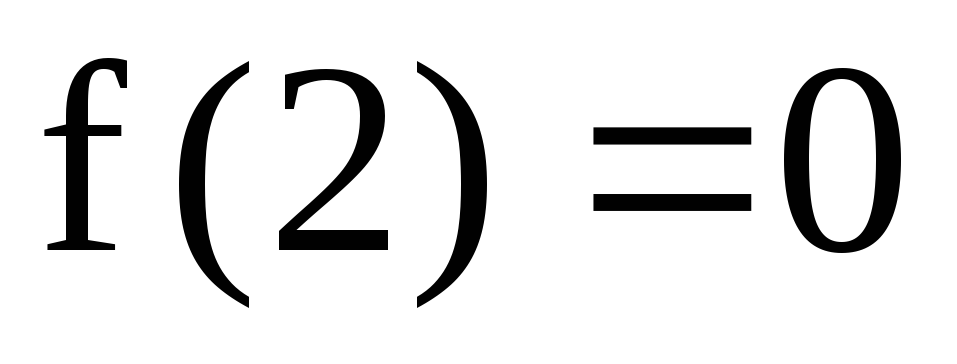 ;
;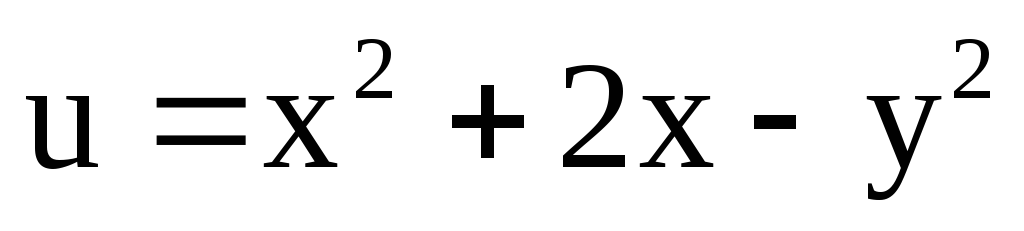 ,
,
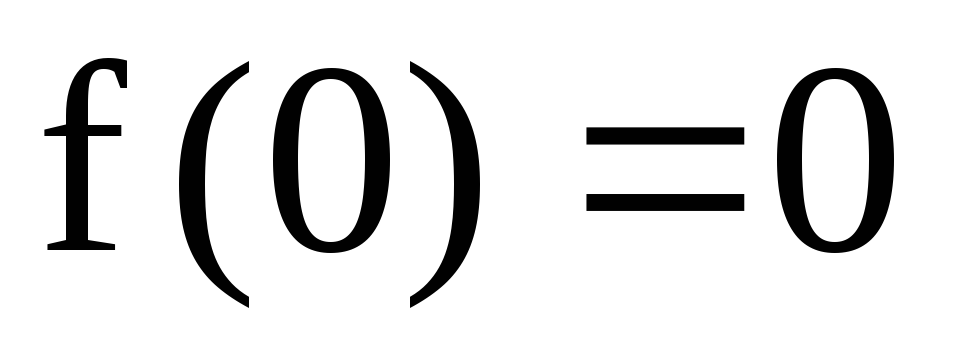 ;
;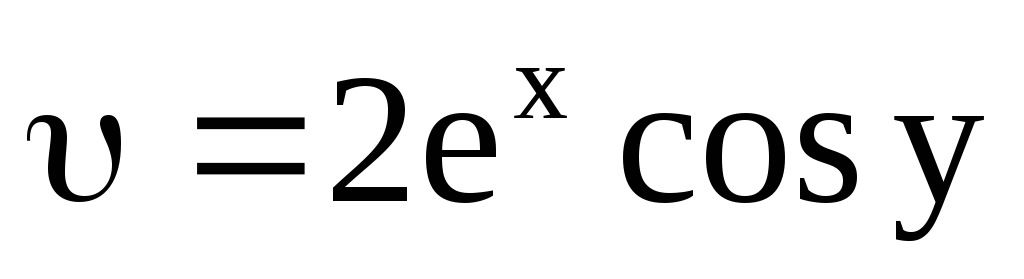 ,
,
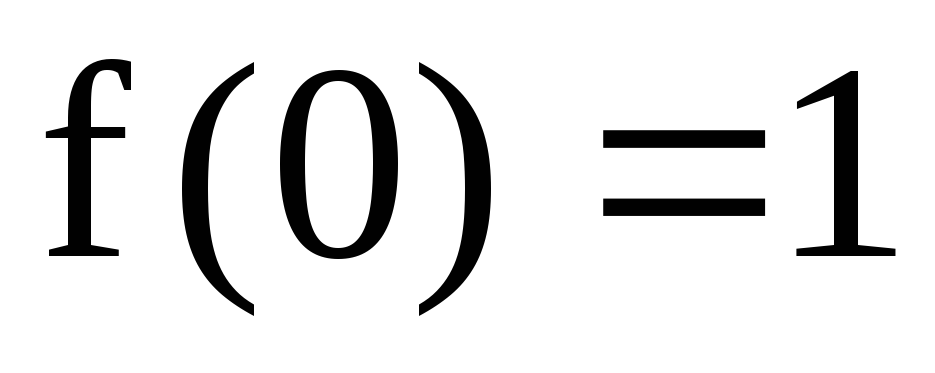 ;
;6.
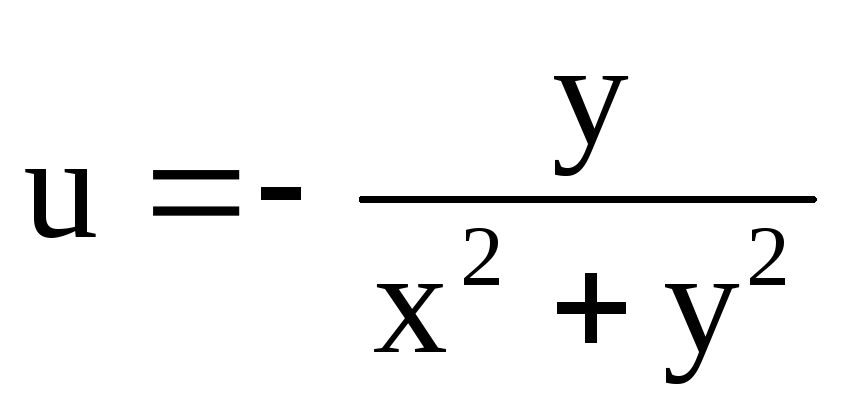 ,
,
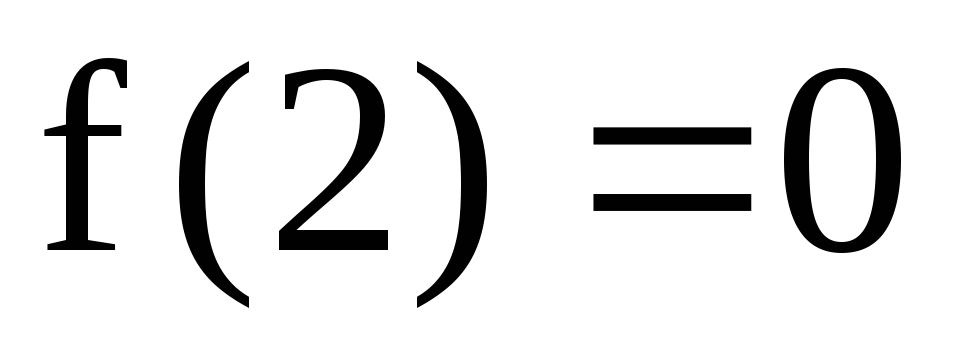 ;
;
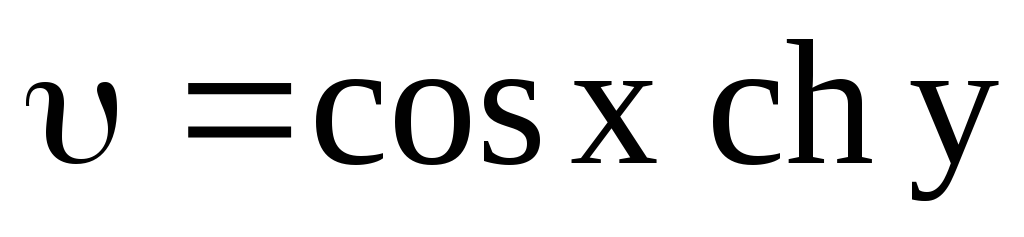 ,
,
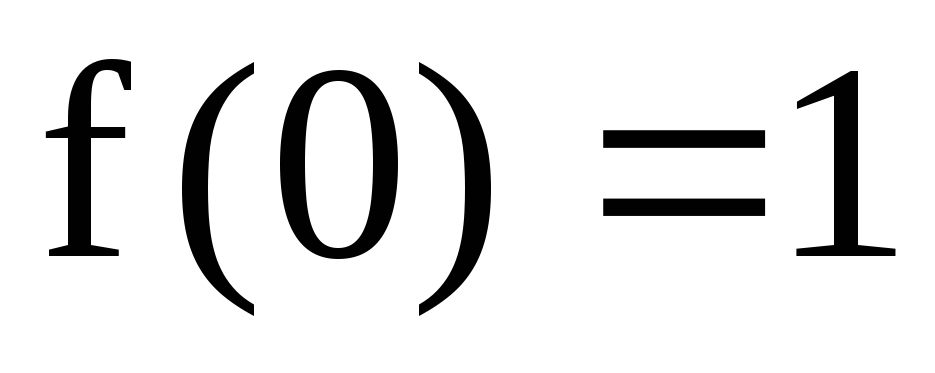 ;
;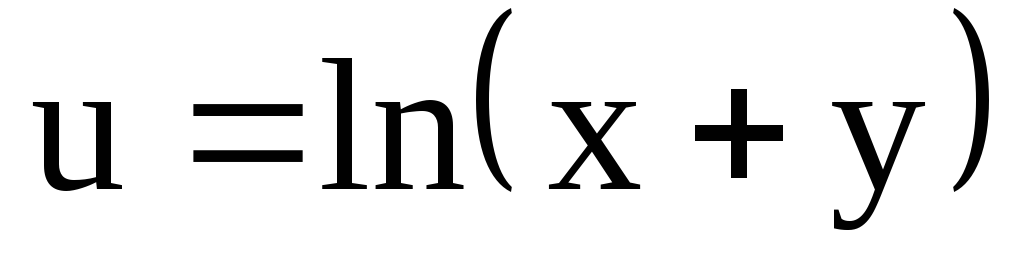 ,
,
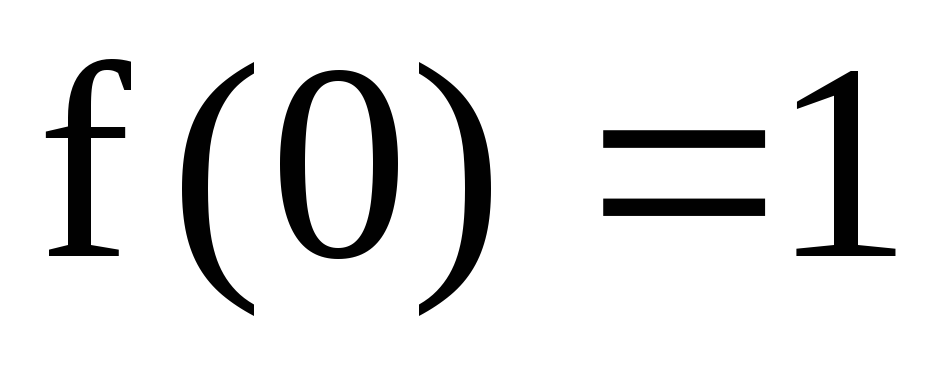 ;
;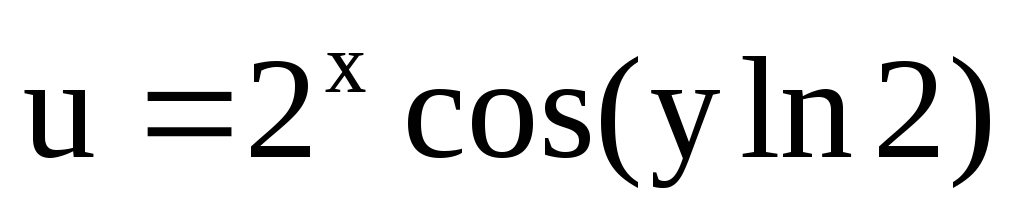 ,
,
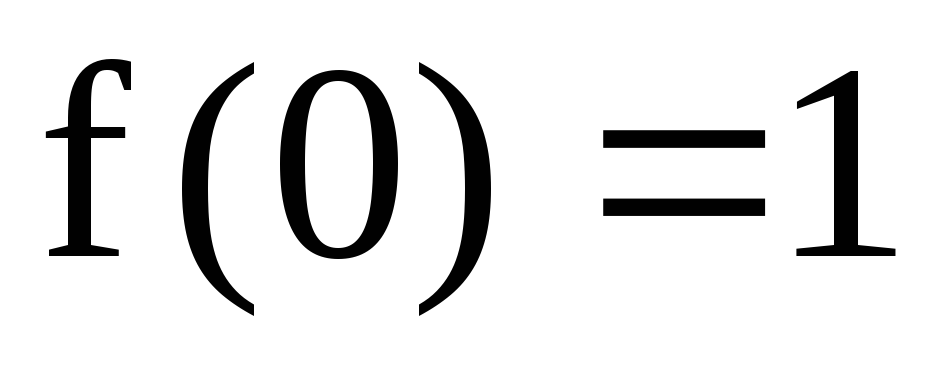 ;
;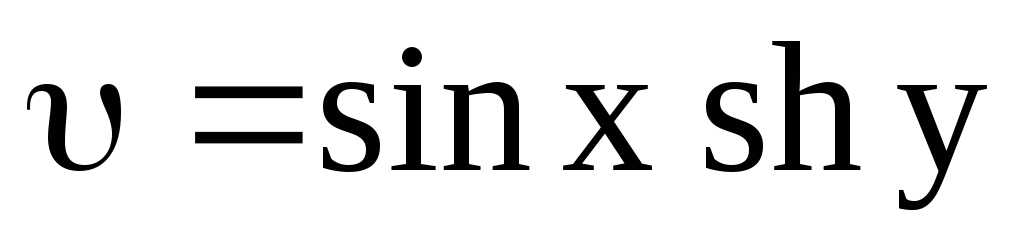 ,
,
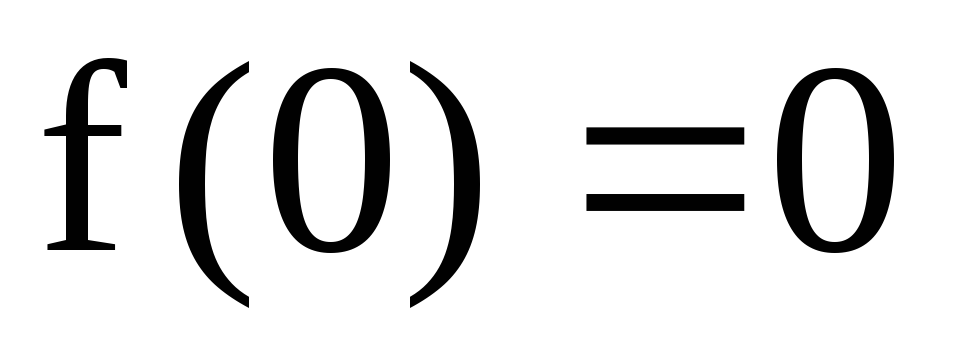 .
.
Задание
№ 2.
Найти области,
на которые функция Жуковского ![]() отображает:
отображает:
круг
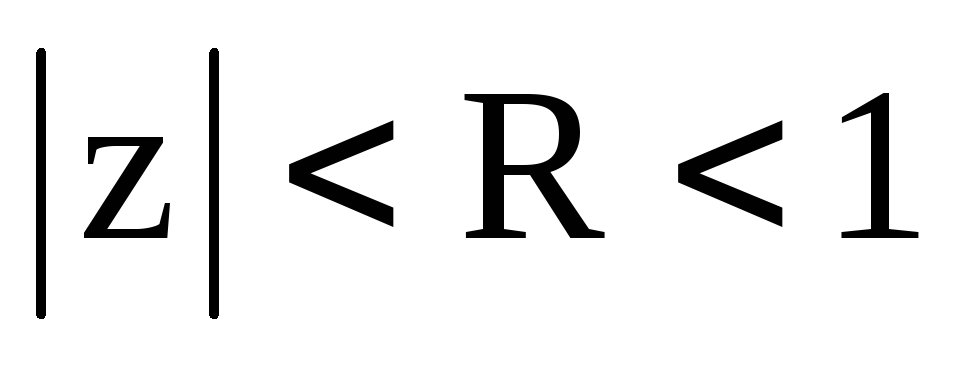 ;
;область
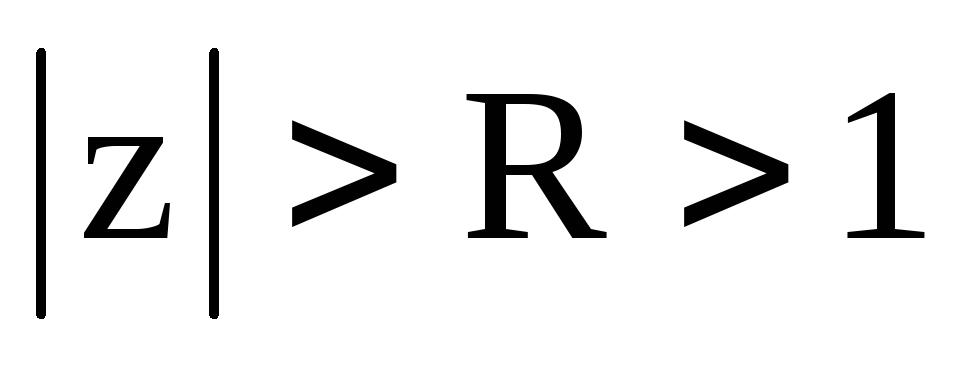 ;
;круг
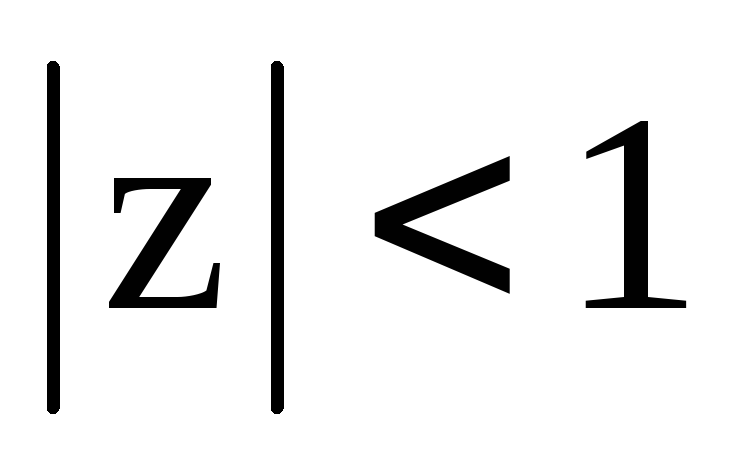 ;
;область
 ;
;полуплоскость
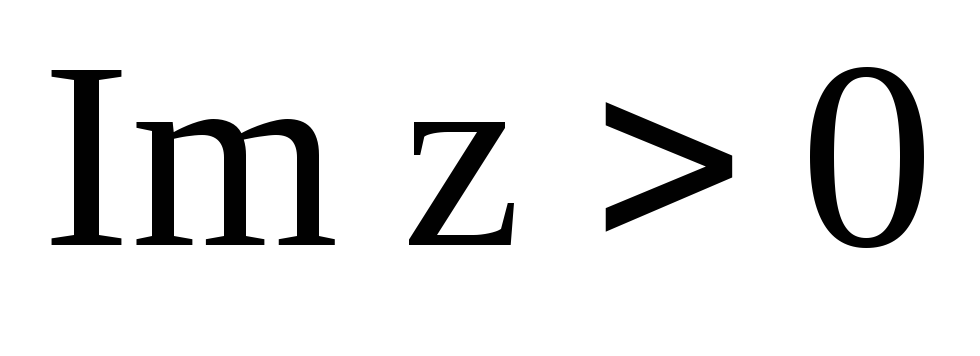 ;
;полуплоскость
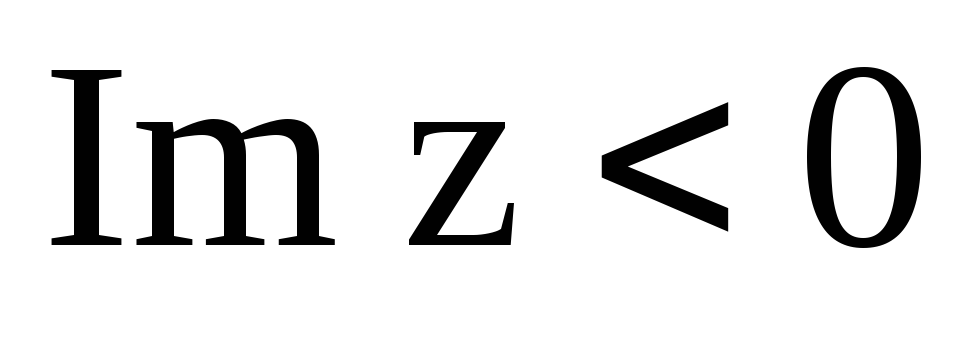 ;
;полукруг
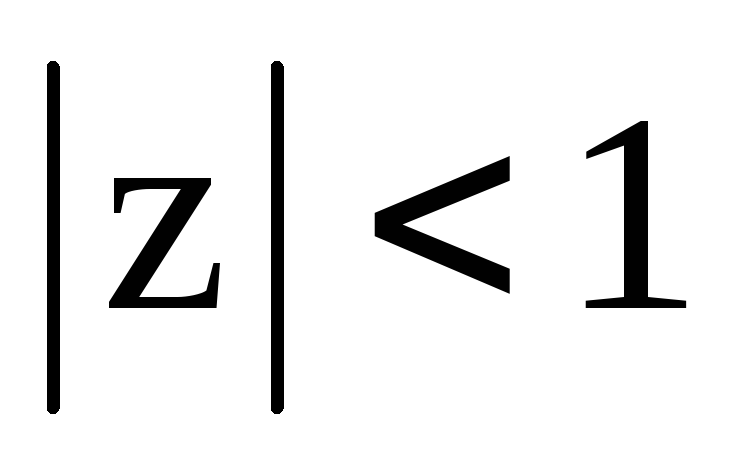 ,
,
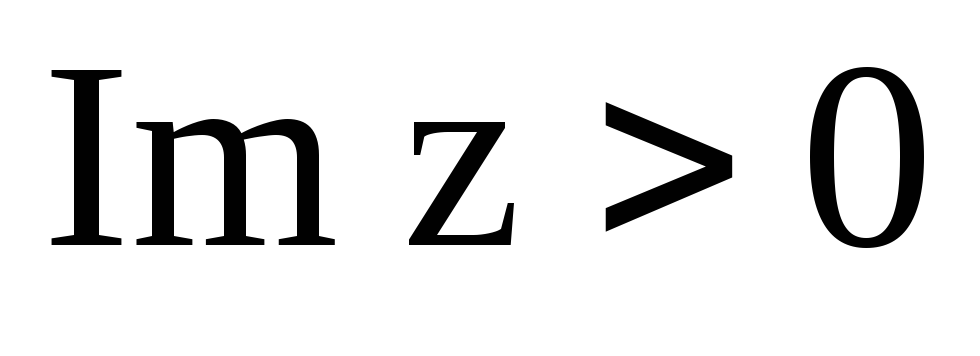 ;
;полукруг
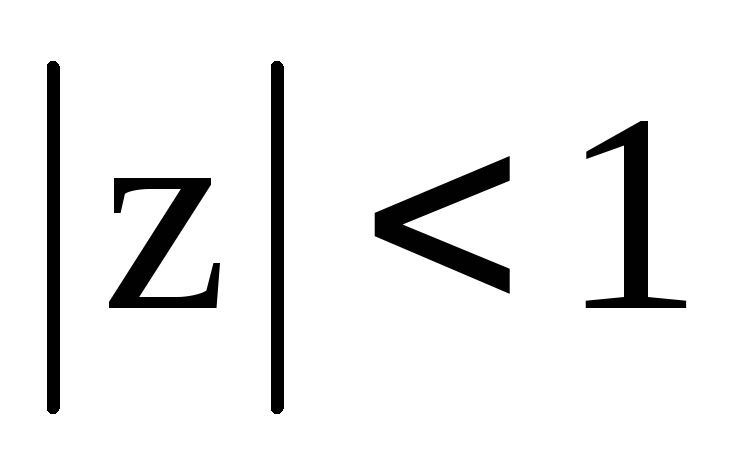 ,
,
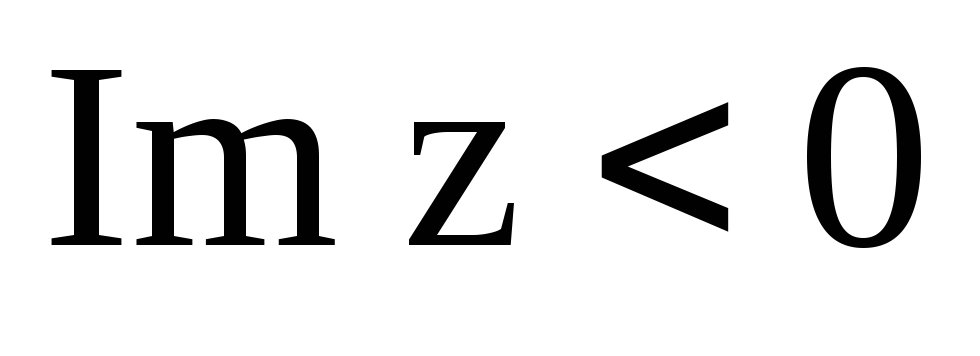 ;
;область
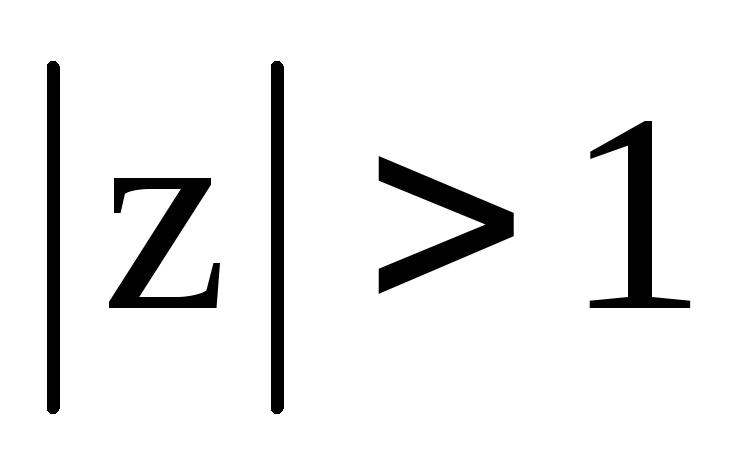 ,
,
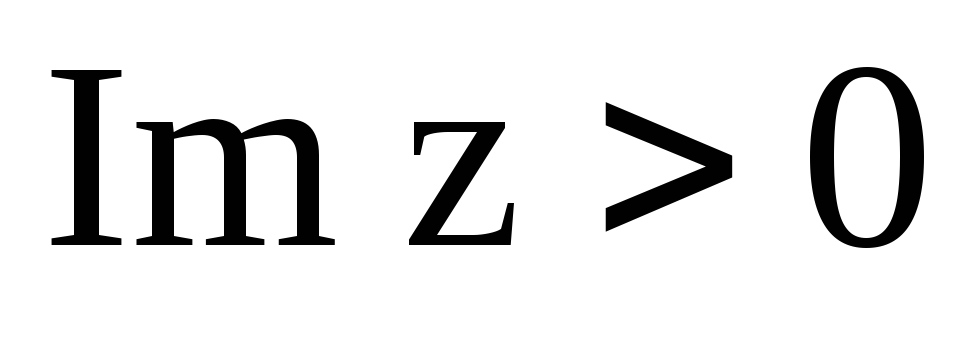 ;
;область
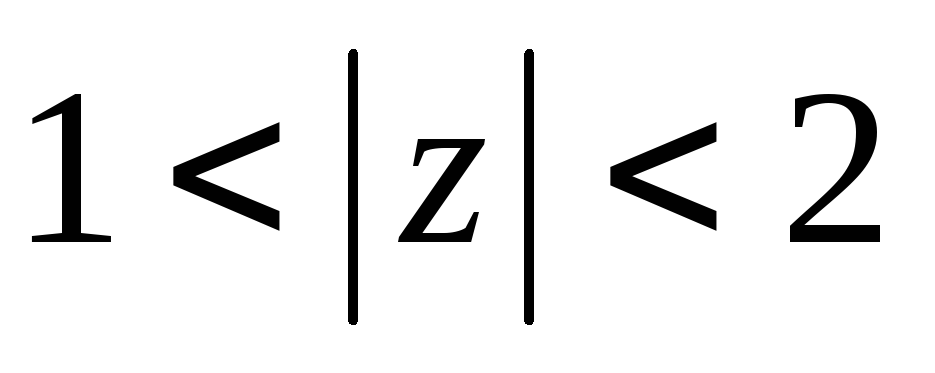 ,
,
 .
.
Задание
№ 3.
Используя
интегральную формулу Коши, теорему
Коши для многосвязной области и
интегральную формулу для производных
аналитической функции, вычислить по
указанному в скобках контуру ![]() (обход против часовой стрелки) следующие
интегралы:
(обход против часовой стрелки) следующие
интегралы:
 ,
,
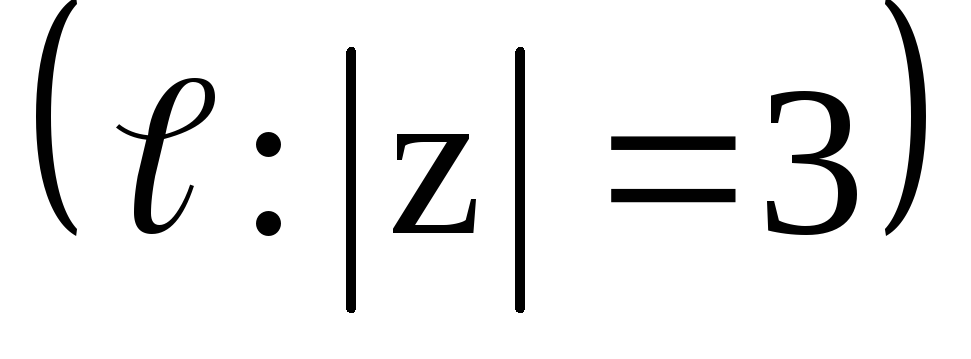 ;
;
2.
![]() ,
,
![]() ;
;
3.
![]() ,
,
![]() ;
;
4.
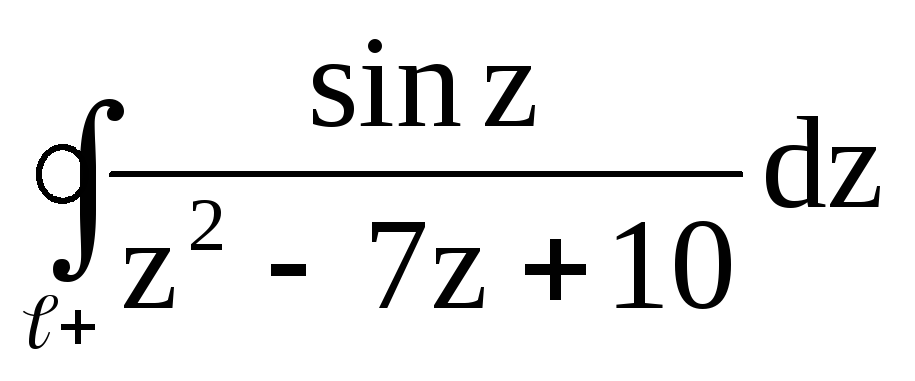 ,
,
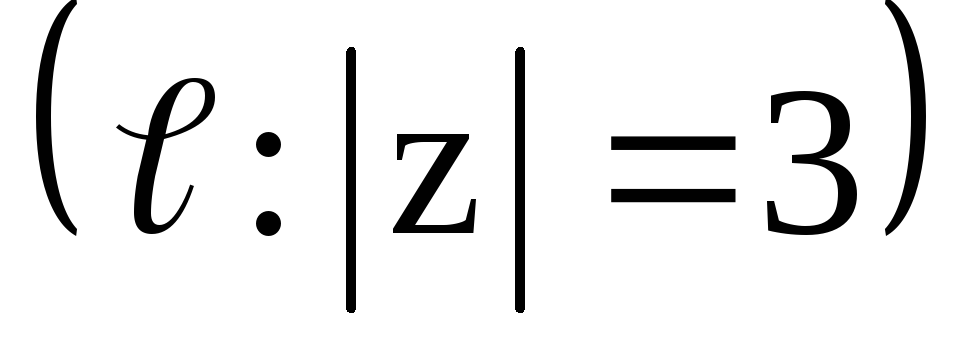 ;
;
5.
![]() ,
,![]() ;
;
6.
![]() ,
,
![]() ;
;
7.
![]() ,
,
![]() ;
;
8.![]() ,
,
![]() ;
;
9.![]() ,
,
![]() ;
;
10.![]() ,
,
![]() .
.
Задание
№ 4.
Разложить
в ряд Лорана в окрестностях точек ![]() ,
указанных в скобках, следующие функции:
,
указанных в скобках, следующие функции:
1.
![]() ,
,
![]() ;2.
;2.
2.
![]() ,
,
![]() ;
;
3.
![]() ,
,
![]() ;
;
4.
![]() ,
,
![]() ;
;
5.
![]() ,
,
![]() .
.
Разложить
в ряд Лорана по степеням ![]() в кольце D
(точка
в кольце D
(точка ![]() и кольцо D
указаны в скобках) следующие функции:
и кольцо D
указаны в скобках) следующие функции:
6. , ;
7.
![]() ,
,
![]() ;
;
8.
![]() ,
,
![]() ;
;
9. , ;
10. , .
Задание № 5. Полагая, что обход замкнутых контуров происходит в положительном направлении, вычислить с помощью вычетов следующие интегралы:
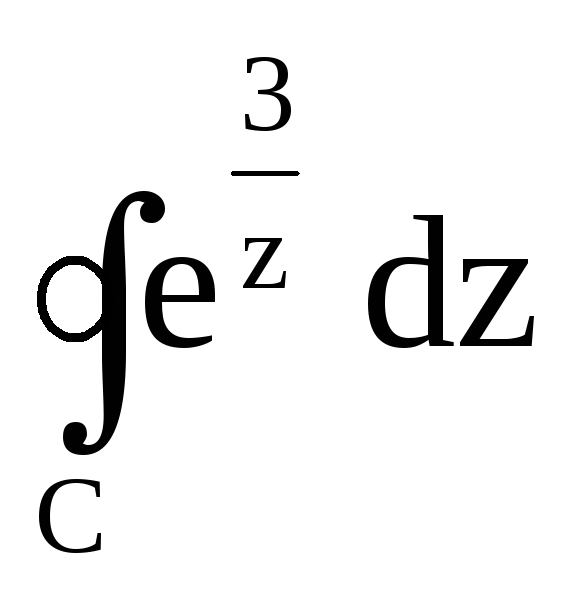 ,
где с – окружность
,
где с – окружность 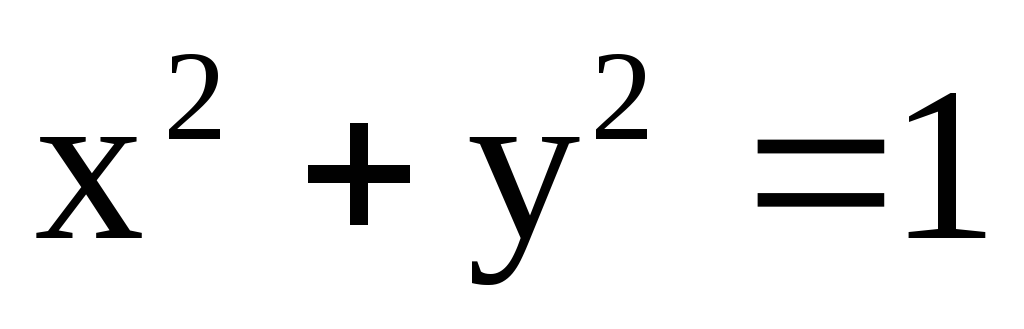 ;
;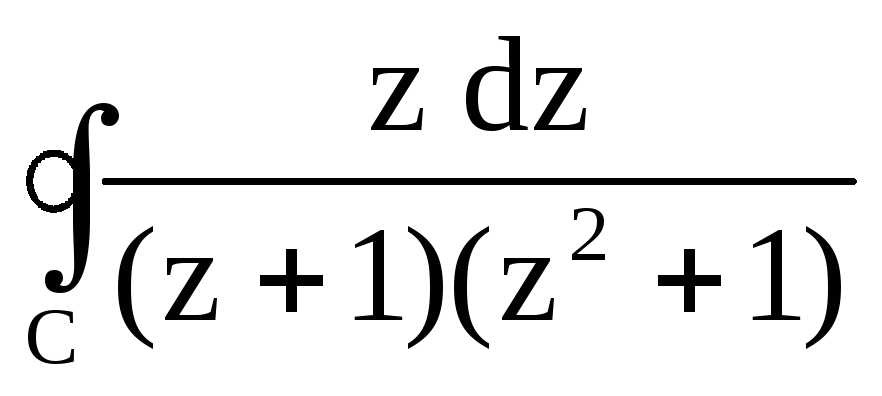 ,
где с – окружность
,
где с – окружность  ;
;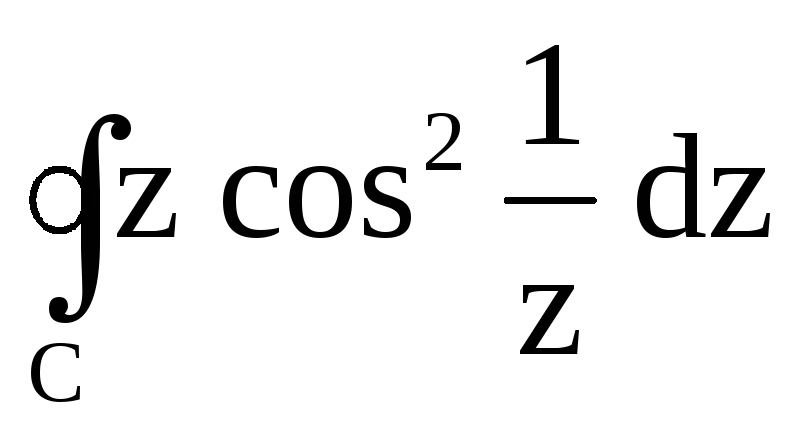 ,
где с – окружность
,
где с – окружность 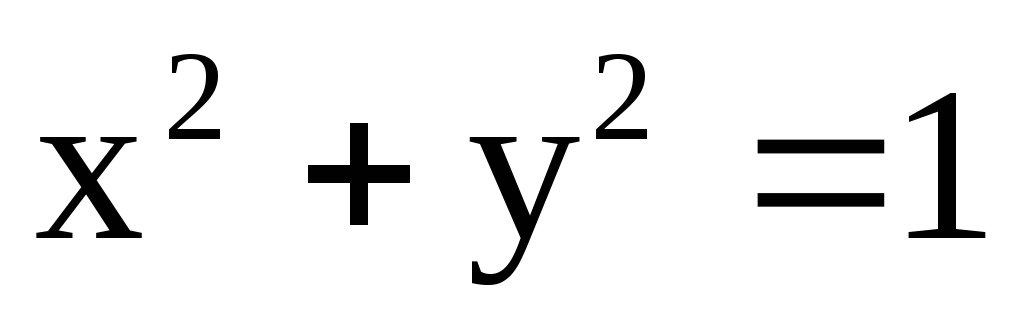 ;
;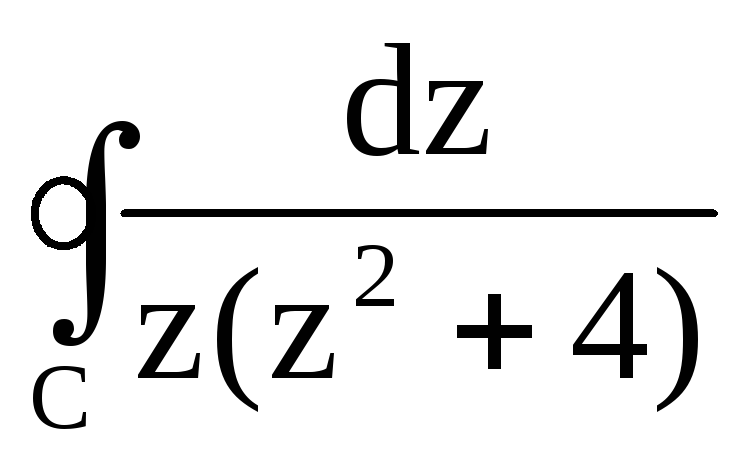 ,
где с – окружность
,
где с – окружность 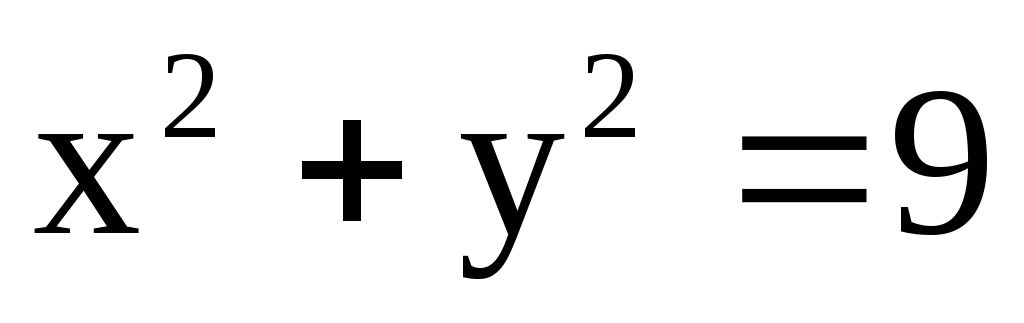 ;
;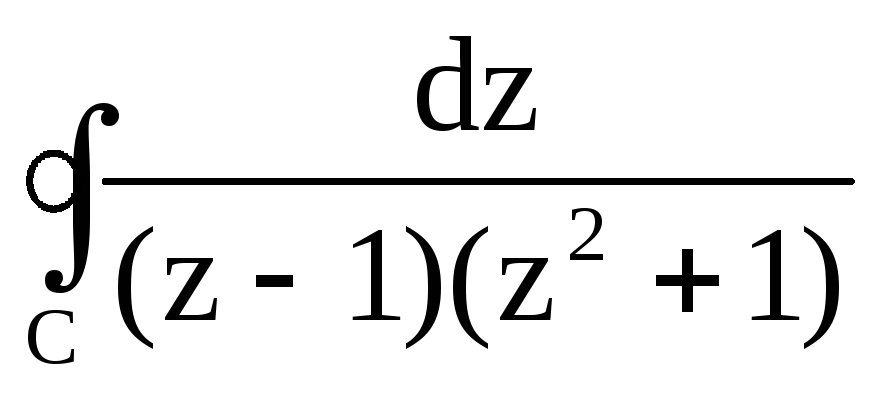 ,
где с – окружность
,
где с – окружность 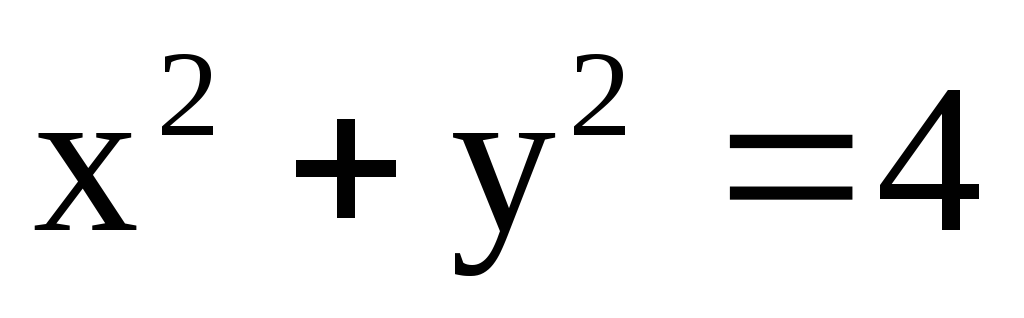 ;
;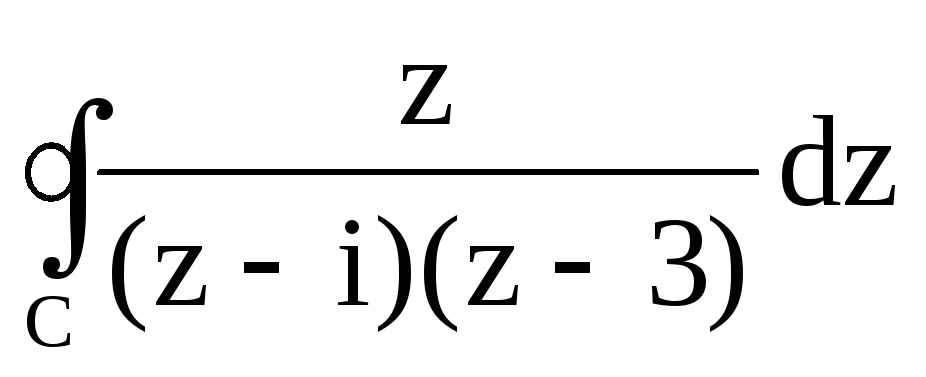 ,
где с – окружность
,
где с – окружность  ;
;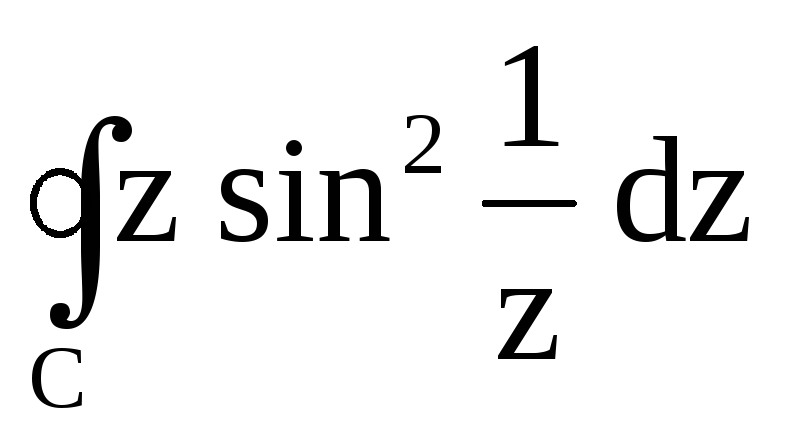 ,
где с – окружность
,
где с – окружность 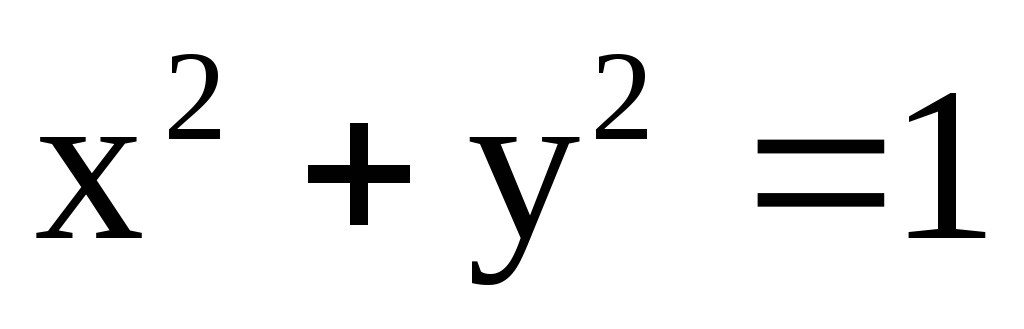 ;
;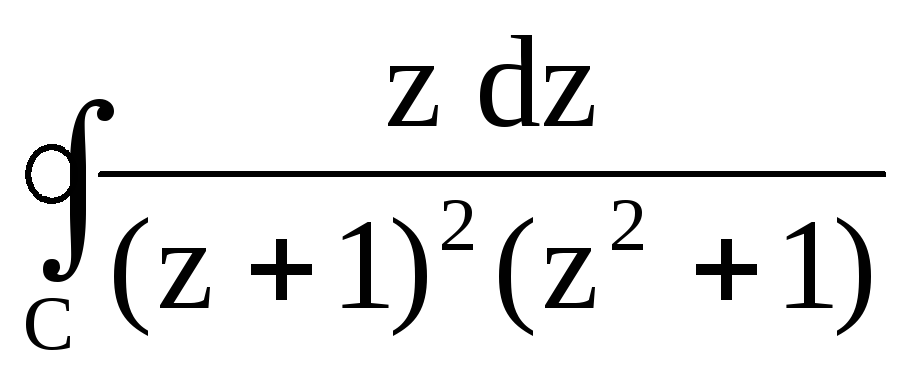 ,
где с – окружность
,
где с – окружность  ;
;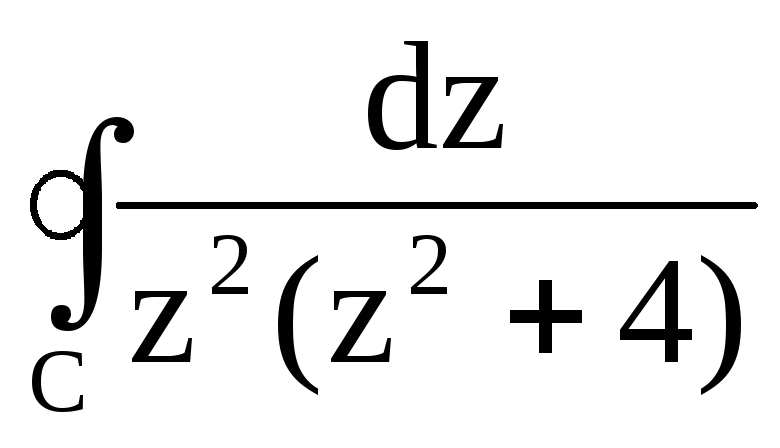 ,
где с – окружность
,
где с – окружность 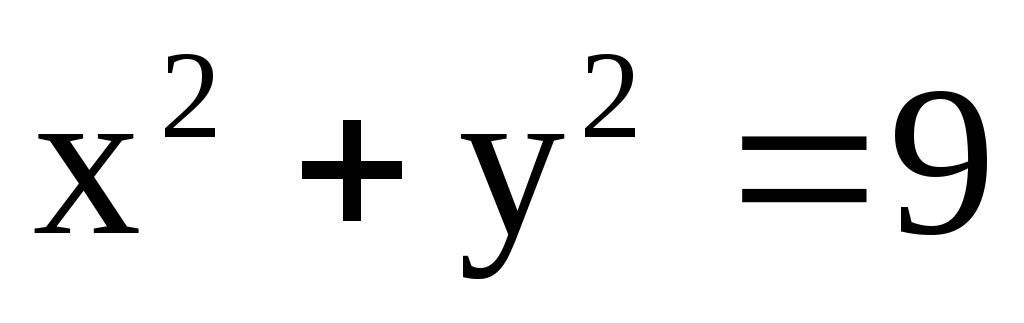 ;
;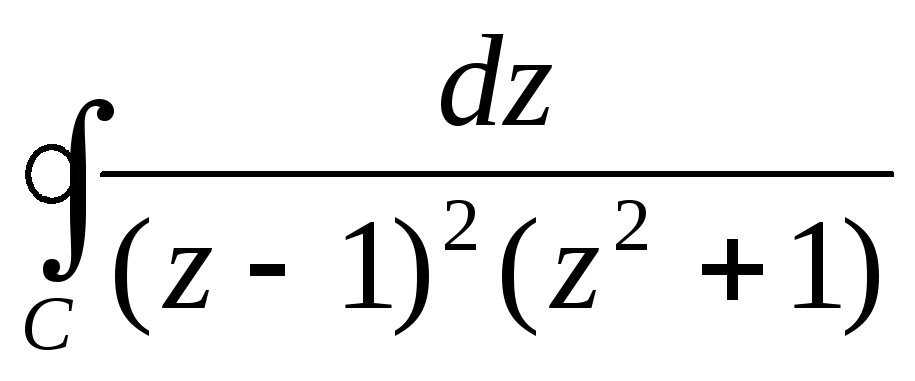 ,
где с – окружность
,
где с – окружность 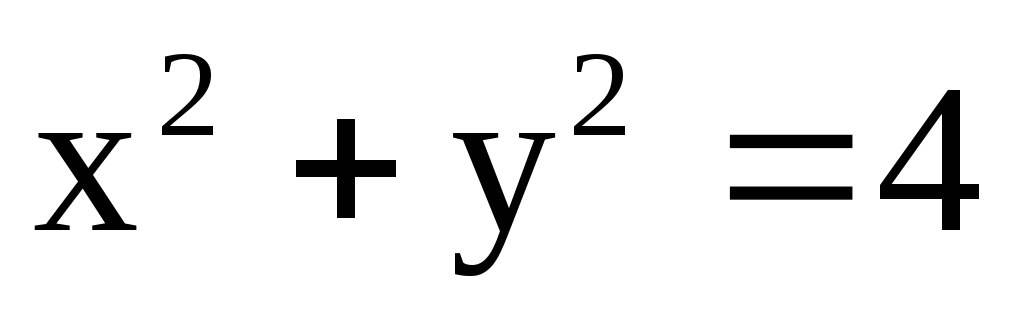 .
.
Контрольная работа № 11
Задание № 1. По заданным оригиналам найти изображения следующих функций:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.![]()
Задание № 2. По заданному изображению найти оригинал следующей функции:
![]() ,
,
где a – последняя цифра зачетной книжки, b – предпоследняя цифра зачетной книжки.
Задание № 3. Найти частные решения уравнения, удовлетворяющие указанным начальным условиям:
![]()
![]()
![]()
где a – последняя цифра зачетной книжки, b – предпоследняя цифра зачетной книжки.
Задание № 4. Найти частные решения системы линейных дифференциальных уравнений, удовлетворяющие указанным начальным условиям:
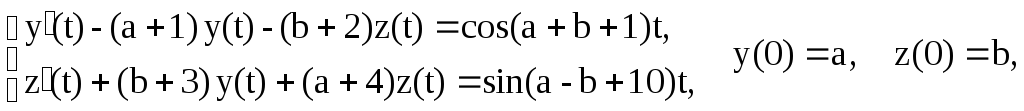
где a – последняя цифра зачетной книжки, b – предпоследняя цифра зачетной книжки.
Задание № 5. На вход цепи, изображенной на рисунке:

в
момент ![]() подается прямоугольный импульс высотой
подается прямоугольный импульс высотой
![]() и длительностью
и длительностью ![]() .
Определить выходное напряжение, зная,
что операторный коэффициент передачи
равен:
.
Определить выходное напряжение, зная,
что операторный коэффициент передачи
равен:
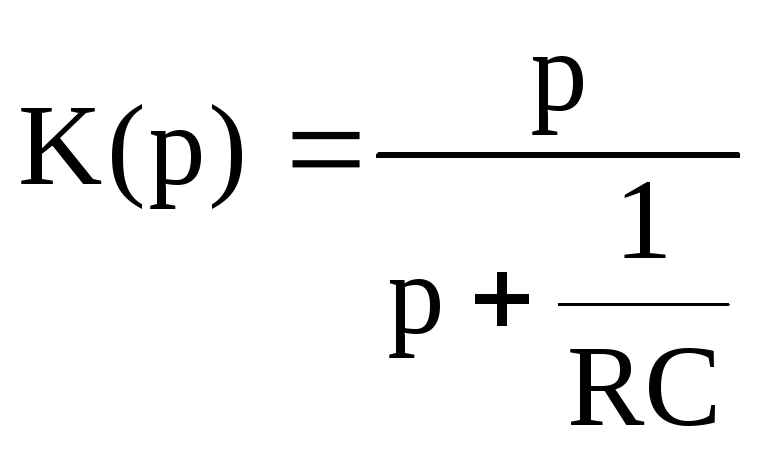 ,
, ![]() ,
,
![]() ,
,
где a – последняя цифра зачетной книжки, b – предпоследняя цифра зачетной книжки.
