2.4 Методы численного интегрирования.
i |
x |
y(x) |
xср |
уср |
|
|
0 |
1,2 |
0,704327 |
|
|
h= |
0,1 |
1 |
1,3 |
0,781203 |
1,25 |
0,742785 |
a= |
1,2 |
2 |
1,4 |
0,857869 |
1,35 |
0,819567 |
b= |
2 |
3 |
1,5 |
0,934262 |
1,45 |
0,896102 |
|
|
4 |
1,6 |
1,010351 |
1,55 |
0,972345 |
|
|
5 |
1,7 |
1,086129 |
1,65 |
1,048279 |
|
|
6 |
1,8 |
1,161596 |
1,75 |
1,123901 |
|
|
7 |
1,9 |
1,236766 |
1,85 |
1,199217 |
|
|
8 |
2 |
1,311652 |
1,95 |
1,274243 |
|
|
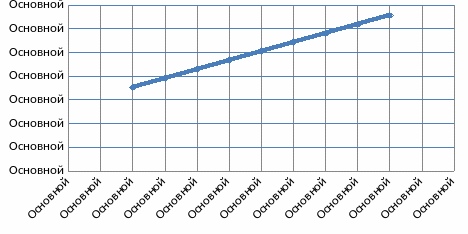
Правые прямоугольники.
Левые прямоугольники.
Средние прямоугольники.
Трапеции.
Ipp= |
0,837983 |
Ilp= |
0,77725 |
Isp= |
0,807644 |
Itr= |
0,807616 |
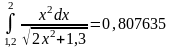
Самыми точными методами оказались методы средних прямоугольников и трапеций.
Заключение.
В этой курсовой работе мною была предоставлена тема по теоретической части «Методы решения дифференциальных уравнений. Обзор». В практической части мной были разобраны численные методы решения нелинейных уравнений, систем нелинейных уравнений, решение интеграла и аппроксимация случайной величины в среде MS Exel. В ходе данной работы я изучил оболочку MS Exel и могу сказать, что в MS Exel сделан большой упор на организованность информации и линейность.
Список литературы.
Лапчик, М. П. Численные методы: учебное пособие для студентов высших учебных заведений / М. П. Лапчик, М. И. Рагулина, Е. К. Хеннер; под редакцией М. П. Лапчик. 5-е изд., стер.-М.: Издательский центр «Академия», 2009 – 384с.
Символоков, М. В. Решение бизнес-задаx в Microsoft Office – М.: ЗАО «Издательство БИНОМ», 2001г.