§5. Теорема о движении центра масс смт

Считая, что массы МТ постоянны, преобразуем формулу (4.4) для количества движения СМТ следующим образом:

. (5.1)

На основании формулы (3.3) можно получить:

(5.2)

Подставляя соотношение (5.1) в (5.2), получим:

итак,

. (5.3)

Таким образом, количество движения СМТ равно количеству движения, которое имел бы центр масс СМТ, если бы в нем была сосредоточена вся масса СМТ.

Подставляя (5.3) в (4.5), получим теорему о движении центра масс СМТ в векторной форме:

(5.4)

Теорема: Центр масс СМТ движется как МТ, в которой сосредоточена вся масса СМТ и к которой приложены все внешние силы, действующие на СМТ.

Следствия:

• Если , то из первого соотношения формул (5.4) следует, что

.

Если главный вектор внешних сил, действующих на СМТ, равен нулю, то СМТ движется так, что скорость центра масс СМТ постоянна по величине и направлению и равна скорости центра масс в начальный момент времени:

. (5.5)

§ 6. Теорема об изменении кинетического момента смт

Запишем теорему об изменении момента количества движения МТ (1.34) для k-й точки СМТ, учтя, что на нее действуют – равнодействующая всех внешних сил и – равнодействующая всех внутренних сил:

. (k=1,2,...,n)

Просуммировав эти выражения и учитывая, что сумма производных равна производной от суммы, получим:

(6.1)

Используя формулу для главного момента системы сил (Ч.2 Статика) и учтя свойство внутренних сил

, , (6.2)

где - главный момент всех внешних сил, а - главный момент всех внутренних сил относительно какого-либо центра.

Введем понятие кинетического момента СМТ относительно какого-либо центра О.

Определение: Кинетическим моментом или моментом количества движения СМТ называется геометрическая сумма моментов количества движения МТ, входящих в СМТ, относительно того же центра:

. (6.3)

Подставив (6.2) и (6.3) в (6.1), получим теорему об изменении кинетического момента СМТ в следующем виде:

. (6.4)

Теорема: Производная по времени от кинетического момента СМТ относительно какого-либо центра равна главному моменту всех внешних сил, действующих на СМТ, относительно того же центра.

Следствия:

• Если , то из соотношения (6.4) следует, что

.

Если главный момент внешних сил, действующих на СМТ, относительно какого-либо центра равен нулю, то кинетический момент СМТ относительно того же центра постоянен по величине и направлению и равен кинетическому моменту СМТ относительно того же центра в начальный момент времени:

. (6.5)

Соотношение (6.5) выражает закон сохранения кинетического момента для СМТ.

Найдем кинетический момент нмс (атт), вращающейся относительно неподвижной оси Оz

. (6.6)

Величина кинетического момента АТТ, вращающейся относительно неподвижной оси, равна произведению момента инерции АТТ относительно той же оси на угловую скорость АТТ

§ 7. Теорема об изменении кинетической энергии смт

7.1 Три формы теоремы

Просуммировав эти соотношения и учитывая, что производная от суммы равна сумме производных, получим:

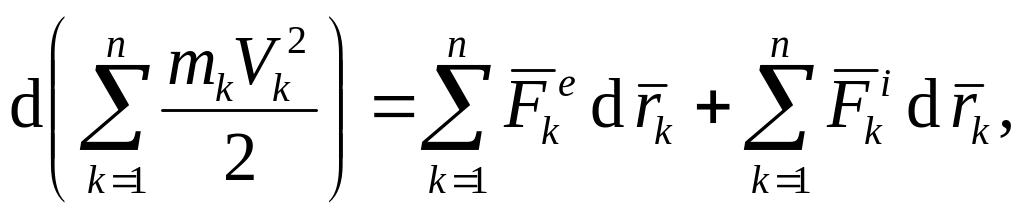
(7.1)

.

Введем понятие кинетической энергии СМТ.

Определение: Кинетической энергией СМТ называется величина, равная сумме кинетических энергий входящих в нее МТ:

, (7.2)

аналогично

. (7.3)

Здесь Т и Т₀ – соответственно значения кинетической энергии СМТ в текущий и начальный моменты времени.

,

соответственно суммы элементарных работ всех внешних и внутренних сил, действующих на СМТ;

,

соответственно суммы их мощностей;

,

соответственно суммы работ всех внешних и внутренних сил, действующих на СМТ.

С учетом принятых обозначений, из соотношений получим три формы (две дифференциальных и одну конечную) теоремы об изменении кинетической энергии СМТ.

Теорема: Дифференциал кинетической энергии СМТ равен сумме элементарных работ всех внешних и внутренних сил, действующих на СМТ.

. (7.4)

Теорема: Производная от кинетической энергии СМТ равна сумме мощностей всех внешних и внутренних сил, действующих на СМТ.

. (7.5)

Теорема: Изменение кинетической энергии СМТ на ее конечном перемещении из одного положения в другое равно сумме работ приложенных внешних и внутренних сил, на том же перемещении.

. (7.6)