2.4. Теорема о моментах инерции относительно параллельных осей – теорема Штейнера-Гюйгенса

Теорема: Момент инерции СМТ относительно любой оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс, и произведения массы СМТ на квадрат расстояния между осями.

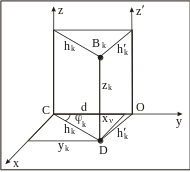
Рис.2

Пусть известен момент инерции СМТ относительно оси Cz, проходящей через ее центр масс С. Найдем момент инерции СМТ относительно оси Оz', параллельной оси z и отстоящей от нее на расстояние d (рис.2)

Начало декартовой системы координат выберем в центре масс С, ось Сy проведем так, чтобы она пересекала ось Оz'.

Возьмем произвольную точку В_k СМТ массы m_k с координатами x_k, y_k, z_k. Расстояние от этой точки до оси Cz – h_k, а до оси Оz' – .

, (2.16)

3. Дифференциальные уравнения движения смт

Пусть СМТ состоит из n МТ с постоянными массами m₁,m₂,…,m_n. Напомним, что через обозначена равнодействующая внешних сил, а через – равнодействующая внутренних сил, действующих на k-ю МТ

Тогда на основании второго (основного) закона динамики в форме (1.2) для каждой МТ можно записать:

(k=1, 2, ..., n). (3.1)

Система (3.1) является системой n дифференциальных уравнений движения СМТ в векторной форме.

Если спроектировать соотношения (3.1) на оси декартовой системы координат, то получим систему 3n дифференциальных уравнений движения СМТ в координатной форме:

k=1, 2, ..., n (3.2)

Следует отметить, что решение задач динамики с использованием системы уравнений (3.2) затруднено тем, что ее уравнения, кроме 3n функций

содержат еще и внутренние силы. Поэтому решение задач динамики с помощью системы уравнений (3.2) может потребовать дополнительных соотношений. Кроме того, значительное количество МТ может привести к громоздкости системы (3.2).

§ 4. Теорема об изменении количества движения смт

Второй основной закон динамики (1.1) для k-й МТ, входящей в СМТ, с учетом классификации сил, действующих на нее, можно записать в форме:

(k=1, 2, ..., n). (4.1)

Просуммировав эти выражения и учитывая, что сумма производных равна производной от суммы, получим:

(4.2)

Используя формулу для главного вектора сил (Гл.1 Статика) и учтя свойство внутренних сил – соотношение (3.2), имеем:

, , (4.3)

где – главный вектор всех внешних сил, – главный вектор всех внутренних сил.

Введем понятие количества движения СМТ.

Определение: Количеством движения СМТ называется геометрическая сумма количеств движений МТ, входящих в СМТ:

. (4.4)

Подставляя выражение (4.3) и (4.4) в соотношение (4.2), получим теорему об изменении количества движения СМТ в дифференциальной форме:

(4.5)

Теорема: Производная по времени от количества движения СМТ равна главному вектору внешних сил, действующих на СМТ.

Умножим обе части соотношения (4.5) на dt:

.

Проинтегрировав это выражение, считая, что в начальный момент времени количество движения СМТ было равно , получим теорему об изменении количества движения СМТ в конечной форме:

. (4.6)

Здесь , – скорость движения k-й МТ в начальный момент времени, а – импульс главного вектора внешних сил или сумма импульсов внешних сил, действующих на СМТ за промежуток времени t:

. (4.7)

Теорема: Изменение количества движения СМТ за конечный промежуток времени равно сумме импульсов всех внешних сил, действующих на СМТ, за тот же промежуток времени.

В проекциях на оси декартовой системы координат эта теорема в конечной форме имеет вид:

,

, (4.8)

т.е изменение проекции количества движения СМТ за конечный промежуток времени равно сумме проекций импульсов всех внешних сил, действующих на СМТ, за тот же промежуток времени.

Следствия:

• Если , то из соотношения (4.6) следует, что

.

Если главный вектор внешних сил, действующих на СМТ, равен нулю, то количество движения СМТ постоянно по величине и направлению и равняется количеству движения СМТ в начальный момент времени:

. (4.9)

Соотношение (4.9) представляет собой закон сохранения количества движения СМТ