Лекции 9-12

Часть 2. Динамика СМТ.

§1.Основные понятия динамики СМТ.

1. 1. Внешние и внутренние силы,

свойства внутренних сил

Пусть СМТ состоит из n МТ (В₁, В₂, …, В_n), массы которых соответственно m₁, m₂,…m_n.

В динамике СМТ вводится следующая классификация сил:

Внешними силами для данной СМТ называются силы, с которыми действуют на нее объекты, не входящие в рассматриваемую СМТ.

Внутренними силами для данной СМТ называются силы взаимодействия между МТ, входящими в рассматриваемую СМТ.

Обозначим через и соответственно равнодействующие внешних и внутренних сил, действующих на k-ю МТ.

Используя этот закон, получим два следующих свойства внутренних сил СМТ:

• главный вектор всех внутренних сил, действующих на СМТ, всегда равен нулю:

; (1.1)

• главный момент всех внутренних сил, действующих на СМТ, относительно произвольного центра всегда равен нулю:

. (1.2)

1.2. Центр масс смт

Определение: Центром масс СМТ называется геометрическая точка C, радиус-вектор которой определяется выражением:

, (1.3)

где М – масса СМТ, которая определяется соотношением:

. (1.4)

Спроектировав соотношение (1.3) на оси декартовой системы координат, получим формулы для координат центра масс СМТ:

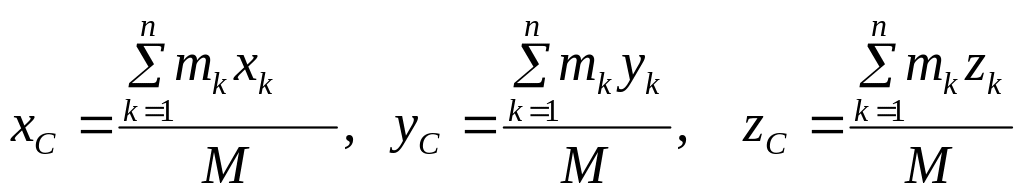. (1.5)

§ 2. Моменты инерции смт

2.1. Определения моментов инерции относительно точки, оси и плоскости

Пусть СМТ состоит из n МТ с массами , ,.…, .

Определения:

Моментом инерции СМТ относительно точки О – J_O называется сумма произведений масс МТ на квадраты их расстояний – до точки О:

. (2.1)

Моментом инерции СМТ относительно оси (например оси z) – называется сумма произведений масс МТ на квадраты их расстояний – h_ до оси z:

. (2.2)

Моментом инерции СМТ относительно плоскости П – J_П называется сумма произведений масс МТ на квадраты их расстояний – d_ до плоскости П:

. (2.3)

Для того чтобы найти моменты инерции для НМС, необходимо НМС разбить на n элементарных частей, записать формулы (3.7) – (3.9) и в них перейти к пределу при n. Тогда получим:

, (2.4) , (2.5)

, (2.6)

где dm – масса элементарной частицы НМС.

2.2. Моменты инерции относительно начала координат, координатных осей и координатных плоскостей декартовой системы координат

Моменты инерции СМТ относительно начала координат, координатных осей и координатных плоскостей декартовой системы координат (рис.1) на основании соотношений (2.1)–(1.3) можно записать в виде:

. (2.7)

Рис.1

(2.8)

(2.9)

Из полученных формул следуют свойства вышеназванных моментов инерции:

(2.10)

2.3. Частные случаи моментов инерции

 Момент инерции однородного тонкого стержня массы М длиной  относительно оси, проходящей через конец стержня перпендикулярно к нему (рис).

Используя соотношение (2.4) и учтя, что , получим:

. . (2.11)

Рис. 24

Если ось z' проходит через середину стержня, то, изменив пределы интегрирования, несложно получить:

. (2.12)

 Момент инерции однородной окружности (тонкого кольца) массы М радиуса  относительно оси, проходящей через центр окружности перпендикулярно ее плоскости (рис. 25).

Рис. 25

Используя соотношение (3.11) и учтя, что

,

получим:

.

. (2.13)

Момент инерции однородного кругового полого цилиндра относительно его оси определяется также по соотношению (2.13).

 Момент инерции однородного тонкого диска массы М радиуса  относительно оси, проходящей через его центр перпендикулярно его плоскости (рис).

Рис

Используя соотношение (2.4) и учтя, что

( – площадь бесконечно тонкого кольца), получим:

. . (2.14)

Момент инерции однородного круглого сплошного цилиндра относительно его оси определяется также соотношением (2.14).

 Радиус инерции. В случае сложной конфигурации НМС его момент инерции определяется экспериментально и может быть выражен через радиус инерции. В этом случае момент инерции определяется по формуле:

, (2.15)

где ­­­­­– радиус инерции.