Преобразования графиков
Приведем графики некоторых функций:
1)
– прямая линия; 2)
– квадратичная парабола;
3)
– кубическая парабола; 4)
– гипербола;
5)
– график квадратного корня;
Правила преобразования графиков:
Пусть
дана функция
1.
Для построения графика функции
исходный график функции
симметрично отображаем относительно
оси Ох
(рис. 1).
2.
Для функции
заданный график симметрично отображаем
относительно оси Оу
(рис. 2).
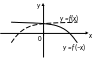
Рис. 1 Рис. 2
3.
Для функции
этот график получается параллельным
переносом графика функции
на
масштабных единиц вдоль оси Оу
вверх, если
и вниз, если
(рис. 3).
4.
Для функции
этот график получается параллельным
переносом графика функции
на
масштабных единиц вдоль оси Ох
вправо, если
и влево, если
(рис. 4).
Рис. 3 Рис. 4
5.
Для функции
где
график функции
«растянут» в
k
раз вдоль оси Оу
(от оси Ох),
если
«сжат»
в
раз вдоль оси Оу
(к оси Ох),
если
(рис. 5).
Рис. 5
6.
Для функции
где
график
«растянут» вдоль оси Ох
(от оси Оу)
в
раз при
«сжат» вдоль Ох
(к
оси
Оу)
в m
раз, при
(рис. 6).
Рис. 6
7.
Для функции
сохраняется та часть графика функции
которая находится над осью Ох
и на оси Ох,
а та часть, которая находится под осью
Ох,
отображается симметрично оси Ох
в верхнюю полуплоскость (рис. 7).
Рис. 7
8.
Для функции
часть графика функции
соответствующая отрицательному значению
х,
отбрасывается, а неотрицательному –
сохраняется и дополняется симметричной
ей относительно оси Оу
частью (рис. 8).
Рис. 8
Пример
3.4.
Построить график функции
Решение Преобразуем заданную функцию:
Получили
Для построения графика полученной функции используем следующие преобразования:
строим график функции
график функции
получаем из графика функции
путем движения его на единицу влево по
оси Ох;график функции
получаем из предыдущего симметричным
отображением относительно оси Ох;график заданной функции получаем из графика функции параллельным переносом на две единицы вниз по оси Оу (рис. 9).
Рис. 9
Числовая последовательность
Числовой
последовательностью
называется функция, определенная на
множестве натуральных чисел, которая
каждому натуральному числу n
ставит в соответствие число
.
Числовую последовательность обозначают
,
т. е.
–
n-й
член последовательности,
а формула
называется формулой
общего члена последовательности.
Зная
функцию
и номер n,
можно вычислить любой член последовательности.
Пример
3.5.
Определить, является ли число 28 членом
последовательности
если
Решение
Число 28 является членом последовательности,
если найдется такой номер
для которого выполняется равенство
Решим это квадратное уравнение
т. е.
Числа
следовательно, число 28 не является
членом данной последовательности.
Пример
3.6.
Вычислить первые пять членов
последовательности
,
если
.
Определить, для каких членов
последовательности
выполняется условие
.
Решение Подставляя в формулу общего члена значение n = 1, 2, 3, 4, 5, получим:
Решим
неравенство
Решением
этого неравенства будут
Поэтому, для любых членов последовательности
с номерами от 1 до 20 включительно
выполняется условие
