Тригонометрическая форма комплексного числа.

Тригонометрическая форма комплексного числа z = a + bi имеет вид

z = r (cos φ + isin φ)

где r = - модуль комплексного числа,

φ = arg z – аргумент комплексного числа – величина угла между положительным направлением оси Ох и радиус-вектором, изображающем комплексное число.

Нахождение аргумента продемонстрируем в таблице:

Im b 0 а Re	a > 0 b > 0	φ = arctg
Im b a 0 Re	a < 0 b > 0	φ = π – arctg
Im a 0 Re	a < 0 b < 0	φ = π + arctg
Im а 0 Re b	a > 0 b < 0	φ = 2π – arctg

Действия над комплексными числами в тригонометрической форме:

если z₁ = r₁(cosφ₁ + isin φ₁),

z₂ =r₂(cos φ₂ + isin φ₂), то

1. z₁z₂ = r ₁ r ₂(сos (φ₁ + φ₂) + isin (φ₁ + φ₂)),

2. = (cos (φ₁ – φ₂) + isin(φ₁ + φ₂)),

3. формула Муавра (cos φ + isin φ)ⁿ = cos nφ + isin nφ

Пример 1. 9. Выполнить действие над комплексным числом

(1 + i )⁹

Решение

Если число 1 + i возвести в 9-ую степень по правилам действия над комплексными числами в алгебраической форме, то мы не достигнем необходимого результата. В данном случае сначала комплексное число представим в тригонометрической форме, а затем уже возведем в степень. Найдем модель и аргумент комплексного числа z = 1 + i .

r = = 2,

Т. к. a > 0, b > 0, то φ = =

2(cos )

z⁹ = 2⁹ (cos + isin ) = 512 (cos 3π + isin 3π) = 512 ( - 1 + i ^. 0) = - 512

Ответ: - 512

Показательная форма комплексного числа имеет вид

z = re ^iφ

где e ^iφ = сos φ + sin φ – формула Эйлера,

r = - модуль комплексного числа,

φ = arg z – аргумент комплексного числа, вычисление которого смотрите выше.

Действия над комплексными числами в показательной форме:

1. z₁z₂ = r₁r₂ ,

2. = ,

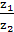3. z ⁿ = r ⁿ e ^inφ

Контрольные вопросы

1. Какую роль играет математика в развитии мировой культуры?

2. Что называется высказыванием?

3. Назовите логические операции над высказываниями.

4. Что определяет знак ?

5. Что называется факториалом числа?

6. Дайте определения множества и операций над множествами.

7. Какие числовые множества вы знаете?

8. Что называется многочленом?

9. Назовите действия над многочленами.

10. Что называется корнем многочлена?

11. Как разложить многочлен на множители?

12. Что называют комплексным числом?

13. Как определяется мнимая единица?

14. Какова алгебраическая форма комплексного числа?

15. Как изображается геометрически комплексное число?

16. Что представляет собой комплексная плоскость?

17. Что называют действительной частью комплексного числа?

18. Что называют мнимой частью комплексного числа?

19. Какие комплексные числа называют сопряженными?

20. Как определяется равенство комплексных чисел?

21. Что следует из равенства a + bi = 0?

22. Каковы правила сложения и вычитания комплексных чисел?

23. Как найти частное двух комплексных чисел?

24. Что называется модулем комплексного числа, как его найти?

25. Что называют аргументом комплексного числа, как его найти?

26. Что представляет собой тригонометрическая форма комплексного числа?

27. Какова формула произведения двух комплексных чисел?

28. Какова формула частного двух комплексных чисел?

29. Что представляет собой формула Муавра?