Элементы комбинаторики

Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, состоящее из k элементов, называется размещением из n элементов по k элементов.

Число размещений из n элементов по k элементов равно произведению k последовательных натуральных чисел от n до n-k+1 включительно, т.е.

или

Размещения из n элементов по n элементов называются перестановками из n элементов.

Число перестановок из n элементов равно n!.

Пусть имеется множество, содержащее n элементов. Каждое его подмножество, состоящее из k элементов, называется сочетанием из n элементов по k элементов.

Число сочетаний из n элементов равно произведению всех натуральных чисел от n до n –k+1 включительно, деленному на k!

Пример 8.2. Группа учащихся изучает 10 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть четыре различных урока?

Решение

Число способов, которыми можно распределить четыре дисциплины из 10, равно числу упорядоченных выборок объёма 4 из множества, содержащего 10 элементов, т.е. числу размещений из 10 элементов по 4. По формуле, полагая в ней n=10, k=4 , получаем

Ответ: 5040.

Пример 8.3. Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз?

Решение

Число матчей равно числу неупорядоченных выборок объема 2 из множества, содержащего 16 элементов, т. е. равно . По формуле числа сочетаний находим

Ответ: 120.

Вероятность и ее свойства

Вероятностью Р(А) события А, связанного с опытом с равновероятными исходами, называется отношение числа исходов, благоприятствующих событию А, к числу всех исходов.

Таким образом, если n - число всех исходов, k - число исходов, благоприятствующих событию А, то

Пример 8.4. В урне находятся 4 черных и 6 белых шаров. Найти вероятность того, что вынутый наудачу шар будет белым.

Решение

Здесь число благоприятных исходов (количество белых шаров k=6), количество всех исходов (количество всех шаров n=10), тогда

Ответ: 0,6.

Пример 8.5. Среди 100 электроламп 5 испорченных. Какова вероятность того, что выбранные наудачу 3 лампы окажутся исправными?

Р ешение

Из 100 электроламп 3 лампы можно выбрать способами. Три исправных лампы из общего числа 95 исправных ламп можно выбрать

способами. Следовательно, искомая вероятность равна

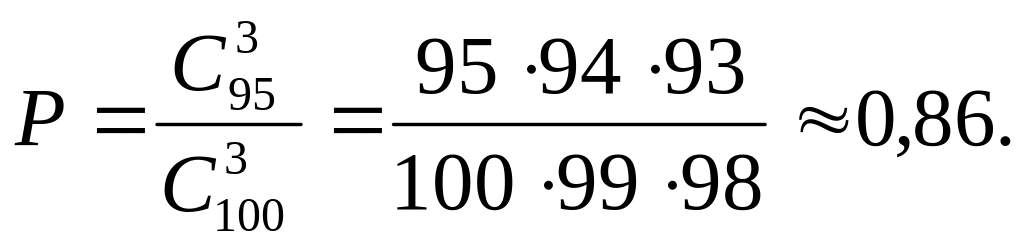
Ответ: 0,86.

Контрольные вопросы

1. Что называется графом?

2. Как определяется степень вершины графа?

3. Назовите свойства степеней вершин.

4. Дайте определение маршруту.

5. Что называется циклом в графе?

6. Какой граф называется эйлеровым?

7. Дайте определение дереву.

8. Какими способами можно задать граф?

9. Что называется размещением и как вычисляется число размещений из n элементов по m элементов?

10. Что называется сочетанием и как вычисляется число сочетаний из n элементов по m элементов?

11. Что называется перестановкой и как вычисляется число перестановок из n элементов?

12. Что называется вероятностью события?

13. Назовите свойства вероятности.

14. Сформулируйте основные теоремы теории вероятностей.