9.3. Оптимальная численность выборки

При организации выборочного обследования следует иметь в виду, что размер ошибки выборки, прежде всего, зависит от численности выборочной совокупности п. Из формулы (4) следует, что средняя ошибка выборки, обратно пропорциональна , т. е. при увеличении, например, численности выборки в четыре раза ее ошибки уменьшаются вдвое.

Вернемся к первому примеру. Отбираем из генеральной совокупности не 5%, а, например, 20% готовой продукции. Численность выборки n будет равна 400 шт.

Тогда, при условии, что = 15,4 г., размер ошибки для выборочной средней, при повторном отборе, составит:

Сопоставляя полученный результат с данными 5% -ного отбора, видим, что ошибка выборки уменьшилась в два раза. Увеличивая численность выборки, можно довести ее ошибку до сколь угодно малых размеров. Можно представить, что при доведении n до размеров N ошибка выборки  становится равной нулю. Но так как при проведении выборочных обследований в торговле определение характеристик выборки в ряде случаев сопровождается разрушением обследуемых образцов, то нормы отбора проб в выборку должны быть минимальными. Это сообразуется с основным преимуществом несплошного наблюдения: получением необходимой информации с минимальными затратами времени и труда. Поэтому вопрос об оптимальной численности выборки имеет важное практическое значение. Повышение процента выборки, как правило, ведет к увеличению объема исследовательской работы, вызывает дополнительные затраты труда и материальных средств. Но, с другой стороны, если в выборку взять недостаточное количество проб (образцов), то результаты исследования могут содержать большие погрешности. Все это необходимо учитывать при организации выборочного обследования.

Определение необходимой численности выборки основывается на формуле предельной ошибки выборки. Так, применительно к формуле

объем необходимой выборки можно получить путем преобразований, решая это равенство относительно n

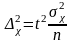(23)

Отсюда необходимая численность выборки при расчете средней величины количественного признака (назовем ее n_) выразится так:

(24)

Так же выводят формулу для расчета численности выборки при выборочном обследовании доли альтернативного признака (п_)

(25)

отсюда

(26)

Вывод формул для определения численности выборки при бесповторном отборе аналогичен. Здесь также преобразования сводятся к определению значения n из формул (14) и (15).

Конечный результат для бесповторного отбора будет таким:

а) для доли альтернативного признака

(27)

б) для средней величины количественного признака

(28)

Расчет оптимальной численности выборки проиллюстрируем на данных первого примера.

Пример. Исходя из требований ГОСТа, необходимо установить оптимальный объем выборки из партии нарезных батонов (2000 шт.), чтобы с вероятностью 0,997 предельная ошибка не превысила 3% веса 500-граммового батона. Заданную ГОСТом относительную ошибку выборки выразим абсолютной величиной:

500 ( 3)

 = = 15 г.

100

Подставляя это значение в формулу (28), получаем:

2000  3²  15,4²

n_ = ——————————10 шт

200015²+3²15,4²