9.1. Ошибка выборки
В связи с тем, что изучаемые статистикой признаки варьируют, т. е. товар состоит из неодинаковых по качеству и весу изделий, то состав единиц, попавших в выборку, может не совпасть (по изучаемым признакам) с составом изделий во всей партии. Это значит, что обобщающие показатели в выборке ( и ) могут в той или иной мере отличаться от значений этих характеристик в генеральной совокупности (р и ). Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки . В математической статистике доказывается, что значения средней ошибки выборки определяются по формуле
Использование формулы (2) предполагает,
что известна генеральная дисперсия
.
Но при проведении выборочных обследований
эти показатели, как правило, неизвестны.
Применение выборочного метода как раз
и предполагает определение характеристик
генеральной совокупности.
На практике для определения средней
ошибки выборки обычно используются
дисперсии выборочной совокупности
.
Эта замена основана на том, что при
соблюдении принципа случайного отбора
дисперсия достаточно большого объема
выборки стремится отобразить дисперсию
в генеральной совокупности.
В математической статистике доказывается следующее соотношение между дисперсиями в генеральной и выборочной совокупностях:
(3)
Из формулы (3) видно, что дисперсия в
выборочной совокупности меньше дисперсии
в генеральной совокупности на величину
Если n достаточно велико, то отношение близко к единице.
Например, при n=
100 значение
=1,01, а при n=500 значение
=
=
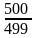1,002 и т.д.
При замене генеральной дисперсии дисперсией выборочной , а формула расчета средней ошибки записывается так:
(4)
При этом для показателя доли альтернативного признака дисперсия в выборочной совокупности определяется по формуле
(5)
Для показателя средней величины дисперсия количественного признака в выборке определяется по формулам:
С
Поскольку при бесповторном отборе
численность генеральной совокупности
N в ходе выборки сокращается, то в формулу
для расчета средней ошибки выборки
включают дополнительный множитель 1 -
Формула
средней ошибки выборки принимает
следующий вид:
(7)
Формулу (7) используем для решения нашего примера, так как она соответствует характеру проведенного при этом обследования. Определим значения средней ошибки выборки:
а) для показателя доли стандартных изделий
б
(
=
15,4 из условия задачи.)
Полученные значения средней ошибки выборочной доли (±0,029) и средней ошибки выборочной средней (± 1,5 г) необходимы для установления возможных значений генеральной доли р и генеральной средней .
Одно из возможных значений, в пределах которых может находиться доля стандартных изделий во всей партии, определяется по формуле
(8)
т. е. р=0,9 ± 0,029, что соответствует значениям от 0,9-0,029=0,871 до 0,9+0,029=0,929.
В общем виде это записывается: 0,871
р
0,929 и читается так: удельный вес стандартных
изделий во всей партии продукции
находится в пределах от 87,1% до 92,9%.
Одно из возможных значений среднего веса изделия по всей партии продукции определяется по формуле
=
(9)
т. е. =500,5 ± 1,5 (г), что соответствует значениям от 500,5-1,5=499 г и до 500,5+1,5=502 г. В общем виде, это записывается так: 499 502, т. е. можно полагать, что средний вес одного изделия во всей партии продукции находится в пределах от 499 г до 502 г.
Полученные таким образом характеристики
доли р и средней
в генеральной совокупности отличаются
от показателей выборочной доли
и средней
на
величины средней ошибки выборки ±
.
Но такое суждение можно гарантировать не с абсолютной достоверностью, а лишь с определенной степенью вероятности.
В математической статистике доказывается, что пределы значений характеристик генеральной совокупности (р и ) отличаются от характеристик выборочной совокупности ( и ) на величину ± лишь с вероятностью, которая определена числом 0,683.
Это означает, что в 683 случаях на 1000 генеральная доля р и генеральная средняя будут находиться в установленных пределах р= ± ,. и = ± В остальных же 317 случаях (1000-683) они могут выйти за эти пределы.
Вероятность суждения можно повысить, если расширить пределы отклонений, приняв в качестве меры среднюю ошибку выборки, увеличенную в t раз.
Так, при удвоенном значении , (т. е. при t =2) вероятность суждения достигает 0,954. Это значит, что только в 46 случаях из 1000 (т. е.1000-954) характеристики могут выйти за пределы двух При этом расширяются и границы характеристик генеральной совокупности. Это можно видеть на данных нашего примера.
При удвоенной средней ошибке выборки изучаемые характеристики во всей партии продукции будут находиться в пределах:
а) доля стандартной продукции
р = ±2 = 0,9 ± 2 • 0,029 . Это соответствует значениям: от 0,9-0,058=0,842 до 0,9+0,058=0,958. В общем виде это записывается так: 842 р 0,958, т, е. с вероятностью, равной 0,954, можно утверждать, что удельный вес стандартных изделий во всей партии (р ) находится в пределах от 84,2% до 95,8%;
б) средний вес одного изделия = ±2 = 500,5 ± 2 • 1,5 , или от 500,5-3,0 г и до 500,5+3,0 г, т. е. с вероятностью 0,954 можно утверждать, что в генеральной совокупности средняя величина веса изделия находится в пределах от 497,5 г до 503,5 г.
Если взять, например, утроенное , то вероятность суждения повышается до 0,997. При этом только в трех случаях из 1000 характеристики генеральной и выборочной совокупностей могут отличаться более чем на 3 . Расчет заданных показателей в этом случае
производится так:
а) для доли стандартных изделий
р = ± З = 0,9 ± 3 • 0,029 ;
б) для среднего веса одного изделия
= ± З = 500,5 ±3.1,5(г).
Таким образом, показатели р и
генеральной совокупности по показателям
выборки
и
определяются:
а) при изучении доли альтернативного признака
p= ± t (10)
б) при изучении средней величины количественного признака
= ± t (11)
Множитель t в формулах (10) и (11) (в статистике он называется коэффициентом доверия) определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного обследования. Итак, в чем же состоит смысл средней ошибки выборки?
Исчисленные характеристики выборочной доли и выборочной средней по своей природе являются случайными величинами. Они могут принимать различные значения в зависимости от того, какие конкретные единицы генеральной совокупности попадут в выборку. Это значит, что в каждом варианте отбора будет различная ошибка выборки. При этом каждый из возможных результатов выборки, а, следовательно, и каждая из возможных ошибок выборки имеют определенную вероятность возникновения. Поэтому средняя ошибка выборки, по существу, представляет среднюю квадратическую величину из отдельных ошибок, взвешенную по вероятности их возникновения.
Для практики выборочных обследований важно, что средняя ошибка выборки применяется для установления предела отклонений характеристик выборки из соответствующих показателей генеральной совокупности небезотносительно. Лишь с определенной степенью вероятности можно утверждать, что это отклонение не превысит величины t , которая в статистике называется предельной ошибкой выборки
Предельная ошибка выборки связана со средней ошибкой выборки отношением:
= t (13)
При этом t как коэффициент кратности средней ошибки выборки зависит от вероятности, с которой гарантируется величина предельной ошибки выборки.
Если в формулу (13) подставить конкретное содержание , то расчет предельной ошибки выборки при бесповторном отборе можно записать следующими алгоритмами:
а) доля альтернативного признака
(14)
6) средняя величина количественного признака
(15)
При этом следует иметь в виду, что
при сравнительно небольшом проценте
единиц, взятых в выборку (до 5%), множитель
близок к единице. Поэтому на практике,
при расчете величины предельной ошибки
выборки при бесповторном отборе множитель
можно
опустить, и расчет производится по
формулам повторного отбора, т. е.
Опуская в формулах (16) и (17) множитель , мы несколько преувеличиваем результаты выборки. Это видно на данных рассматриваемого примера. Так, средняя ошибка выборки по схеме повторного отбора составляет:
а) для доли стандартных изделий
б) для среднего веса изделия
Сравнение этих величин со значениями, полученными при расчете по схеме бесповторного отбора ( =±0,029 и =±1,5),показывает, что разница между ними незначительная.