
- •И.В. Дубограй, о.В. Скуднева, в.Ю. Чуев. Прямая на плоскости Электронное учебное издание
- •Введение
- •1.Уравнение прямой с угловым коэффициентом.
- •2. Общее уравнение прямой.
- •3. Взаимное расположение прямых на плоскости.
- •4. Другие виды уравнений прямой на плоскости.
- •Параметрические уравнения прямой.
- •Каноническое уравнение прямой.
- •Векторное уравнение прямой.
- •Уравнение прямой, проходящей через две точки.
- •Уравнение прямой с нормальным вектором.
- •Уравнение прямой в отрезках.
- •5. Расстояние от точки до прямой.
- •6. Пучок прямых.
- •Задачи для самостоятельной работы.
4. Другие виды уравнений прямой на плоскости.
Определение.
Ненулевой вектор
 называется направляющим
вектором прямой, если он коллинеарен
любому вектору, принадлежащему этой
прямой.
называется направляющим
вектором прямой, если он коллинеарен
любому вектору, принадлежащему этой
прямой.
Положение
прямой
на плоскости можно зафиксировать, задав
точку
 принадлежащую
ей, и направляющий вектор
этой
прямой.
принадлежащую
ей, и направляющий вектор
этой
прямой.
Обозначим
координаты этого вектора
 .
(12)
.
(12)

Тогда,
если произвольная точка
принадлежит прямой
,
то вектор
 коллинеарен направляющему вектору
.
(см. рис. 7). Из условия коллинеарности
двух векторов следует, что
коллинеарен направляющему вектору
.
(см. рис. 7). Из условия коллинеарности
двух векторов следует, что
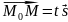 ,
где
,
где
 - параметр, зависящий от положения точки
на прямой и
- параметр, зависящий от положения точки
на прямой и
 .
.
Параметрические уравнения прямой.
Координаты
вектора
 .
Так как векторы
и
.
Так как векторы
и
 равны, их соответствующие координаты
совпадают, то есть
равны, их соответствующие координаты
совпадают, то есть
 и
и
 .
Отсюда следует система двух уравнений,
которая связывает координаты всех точек
прямой
:
.
Отсюда следует система двух уравнений,
которая связывает координаты всех точек
прямой
:
 (13)
(13)
Полученная
система уравнений называется
параметрическими
уравнениями прямой

Каноническое уравнение прямой.
Так как векторы и коллинеарны, их соответствующие координаты пропорциональны (условие коллинеарности векторов). Исходя из этого, выражая параметр из (13), получаем уравнение, которое связывает координаты всех точек прямой :
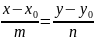 (14)
(14)
Это уравнение называется каноническим уравнением прямой
Пример
8.
Составим каноническое и параметрические
уравнения прямой
 проходящей через точку
проходящей через точку
 пересечения
прямых
пересечения
прямых
 и
и
 параллельно
отрезку
параллельно
отрезку
 где
где

Решение.
Найдём точку пересечения
заданных прямых
 . Для этого составим систему уравнений
этих прямых.
. Для этого составим систему уравнений
этих прямых.
 или
или

Решив
эту систему, получим координаты искомой
точки
 . В качестве направляющего вектора
прямой
возьмём вектор
. В качестве направляющего вектора
прямой
возьмём вектор
 .
И теперь составим каноническое уравнение
прямой
:
.
И теперь составим каноническое уравнение
прямой
:
 (см.
(14)),
а также её параметрические уравнения:
(см.
(14)),
а также её параметрические уравнения:
 (см.(13)).
Ответ:
или
.
(см.(13)).
Ответ:
или
.
Векторное уравнение прямой.
Если
зафиксированная точка
 и произвольная точка
прямой
заданы своими радиус-векторами (см.
рис. 9)
и произвольная точка
прямой
заданы своими радиус-векторами (см.
рис. 9)

 и
и
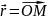 ,
то
,
то
 или
или
 .
.
Отсюда следует, что для радиус-вектора любой точки прямой имеет место уравнение
 .
(15)
.
(15)
Это уравнение называется векторным уравнением прямой
Уравнение прямой, проходящей через две точки.
Если
прямая походит через две точки, заданные
своими координатами
 и
и
 ,
то вектор
,
то вектор
 является направляющим вектором этой
прямой. То есть
является направляющим вектором этой
прямой. То есть
 .
В этом случае из канонического уравнения
(14)
следует уравнение прямой следующего
вида:
.
В этом случае из канонического уравнения
(14)
следует уравнение прямой следующего
вида:
 (16)
(16)
Это уравнение прямой, проходящей через две точки.
Пример
9.
Составим уравнения прямых, на которых
лежат стороны треугольника с вершинами
в точках
 .
.
Решение. Так как на каждой из искомых прямых известны по две точки, составим их уравнения, взяв за основу уравнение вида (16).
Для
уравнения прямой, проходящей через
точки
и
,
за точку с координатами
 примем
примем
 ,
а за точку
,
а за точку
 - точку
.
- точку
.
Тогда
уравнение прямой
 :
:
 , или
, или
 .
.
Аналогично,
уравнение прямой
 :
:
 ,
или
,
или
 .
.
И,
наконец, уравнение прямой
 :
:
 или
или
 , откуда следует:
, откуда следует:

Замечание.
Уравнение прямой
сравним с каноническим уравнением
(14).
Видим, что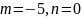 , это координаты направляющего вектора
(см.(12) и рис.8). Так как
, это координаты направляющего вектора
(см.(12) и рис.8). Так как
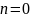 ,
вектор
,
а, следовательно, и сама прямая
перпендикулярны оси
.
Поэтому уравнение этой прямой имеет
вид
,
вектор
,
а, следовательно, и сама прямая
перпендикулярны оси
.
Поэтому уравнение этой прямой имеет
вид
 .
.
Ответ:


