3.2 Расчетные характеристики пути.

Расчеты прочности пути основаны на положении, что его конструкция находится в исправном состоянии, соответствующем требованиям ПТЭ и действующим нормам. Геометрические параметры рельсовой колеи должны соответствовать удовлетворительному состоянию пути.

Важнейшими характеристиками упругих свойств верхнего строения пути являются модуль упругости рельсового основания и коэффициент относительной жесткости рельсового основания и рельса.

Модуль упругости рельсового основания U численно равен равно­мерно распределенной реакции основания, возникающей на единицу длины рельса при упругой осадке основания, равной е

Коэффициент относительной жесткости рельсового основания и рельса:

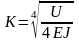
где E – модуль упругости рельсовой стали, E=2,1∙10⁵ МПа

I – момент инерции поперечного сечения рельса в вертикальном направлении, м^-4

U – модуль упругости рельсового основания

Коэффициент относительной жесткости для типовых конструкций пути находится в пределах 0,9...1,8 м^-1, а модуль упругости основания летом 110...167 МПа при железобетонных шпалах. Зимой модуль упругос­ти увеличивается в 1,5...2,0 раза.

Характеристика конструкции пути	План линии	U, МПа	K, 1/м	I в 10 -8, м4
Р65(6)ЖБ, Щ.	На прямой	150	1,536	3208
	На кривой	167	1,578

3.3 Расчетные характеристики подвижного состава.

Динамические силы воздействуют на путь через колеса подвижного состава и рельс. В расчетах учитывают воздействия на путь одной тележки вагона или локомотива. Конструкция экипажной части различных типов подвиж­ного состава должна находиться в исправном состоянии, соответству­ющем требованиям ПТЭ и техническим нормам.

Горизонтальные (боковые) силы, а также крутящие моменты из-за эксцентриситета приложения вертикальных сил в расчетах учитывают­ся коэффициентом, определенным экспериментально.

Тип и серия подвижного состава	Pст , кН	q, кН	Ж, МН/м	f cт , м	d, м	l1, м	Vконстр., м/с
ЧС7	107,5	17,50	1,25	0,169	1,25	3,20	44,4
ВЛ60	115,0	30,80	1,16	0,061	1,25	2,3	27,7

Р_ст— статическая нагрузка от колес на рельс;

q_k — отнесенный к колесу вес необрессоренных частей;

Ж— приведенная к колесу жесткость рессорного подвешивания;

f_ст — статический прогиб рессорного подвешивания;

d — диаметр колеса по кругу катания;

l₁ — расстояние между центрами осей колесных пар тележки экипажа;

V_{констр.} — конструкционная скорость.

3.4 Определение вертикальных динамических сил, действующих на рельс.

Расчетная сила слагается из постоянной величины статической на­грузки на колесо и переменных дополнительных сил инерции от коле­баний экипажа

P_расч = P_ст + Р_р + P_нп + P_инк + P_ннк

где P_ст , Р_р , P_нп , P_инк , P_ннк – составляющие соответственно от веса экипажа, колебаний кузова на рессорах, сил инерции необрессореных масс при изолированных неровностях на пути и колесах, а также непрерывных неровностях на колесах.

Статическая нагрузка принимается постоянной, а остальные явля­ются случайными или статистическими величинами.

Расчет ведется на максимально вероятное значение динамичес­кой нагрузки

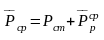
где 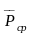- среднее значение вертикальной нагрузки;

- статическая нагрузка колеса на рельс, Н;

- среднее значение вертикальной составляющей сил инерции от колебания кузова на рессорах, Н;

- нормирующий множитель, определяющий появление максимальной дина­мической нагрузки;

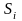- среднее квадратическое отклонение от сил инерции, Н.

Нормирующий множитель принят = 2,5, что гарантирует уровень вероятности 0,994, т.е. из 1000 случаев прохода колеса в расчетном сечении только в 6 случаях возможно превышение

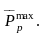
Для вагонов и для старых единиц подвижного состава максимальное значение сил инерции Р_р от колебания кузова на рессорах считается по следующей формуле:

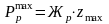
где Ж_p – жесткость комплекта рессор, отнесенная к одному колесу, Н/м;

z_max – максимальный динамический прогиб рессор, мм;

z_max = a_р + b_p ∙ V²

где a_р и b_p – коэффициенты определяемые по таблице.

Для современных единиц подвижного состава применяется следующая формула расчета :

можно принять среднее значение

где k_д – динамический коэффициент;

q_k – отнесенный к колесу вес необрессоренной части экипажа, Н;

V – расчетная скорость экипажа, км/ч;

f_ст – общий статистический прогиб рессор, мм;

Среднее квадратическое отклонение динамической нагрузки колеса на рельс S определяется по формуле композиции законов распределе­ния его составляющих

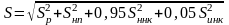
где S_p — среднее квадратическое отклонение динамической нагрузки колеса на рельс от вертикальных колебаний надрессорного строения, Н;

S_нп — среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс при прохождении колесом изоли­рованной неровности пути, Н;

S_ннк — среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс, возникающих из-за непре­рывных неровностей на поверхности катания колес, Н;

S_инк — среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс, возникающих из-за наличия на поверхности катания колес плавных изолированных неровностей, Н;

0,05 — количество колес рассчитываемого типа, имеющих изолированные плавные неровности на поверхности катания, отнесенное к общему числу таких колес, %, эксплуатируемых на участке;

0,95 — количество колес, %, имеющих непрерывную плавную неровность на поверхности катания.

Среднеквадратическое отклонение динамической нагрузки колеса на рельс от вертикальных колебаний надрессорного строения определяется по формуле:

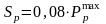
Среднеквадратическое отклонение сил инерции, возникающих при движении колеса по изолированной неровности пути,

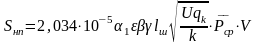
где α₁ — коэффициент, учитывающий величину колеблющейся массы пути (железобетонные шпалы — 0,931);

ε — коэффициент учета жесткости пути (железобетон­ные шпалы —0,322);

β — коэффициент, зависящий от типа рельсов (для рельсов Р65 он равен 0,87);

ϒ — коэффициент учета рода балласта (щебень, асбест, сортированный гравий — 1);

l_ш — расстояние между осями шпал (при эпюрах укладки 2000,1840; l_ш соответственно 0,5м; 0,55м).

Среднеквадратическое отклонение сил инерции, возникающих от непрерывной неровности колеса, определяются по формуле:

где α₀ – коэффициент учета взаимодействия массы пути и необрессоренной массы экипажа;

d – диаметр колеса, м.

Среднеквадратическое отклонение сил инерции, возникающих при движении колеса по изолированной неровности пути:

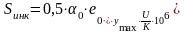
где e₀ – расчетная глубина изолированной неровности, принимаемая 2/3 от наибольшей глубины ползуна на колесах по ПТЭ (для локомотивов e₀ = 0,047∙10^-2 м);

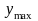=1,47