1.3 Расчет переходных кривых

Прямые и круговые кривые во избежание внезапного появления центробежной силы должны сопрягаться плавно с помощью переходных кривых. Основное назначение переходных кривых заключается в обеспечении плавного изменения центробежных, сил при входе экипажей в круговую кривую и выходе из нее. На их протяжении осуществляют плавные отводы возвышения наружной рельсовой нити и уширения колеи в круговой кривой. Схема переходной кривой в увязке с отводом возвышения наружной рельсовой нити и изменением центробежной силы представлена на рисунке 1.4

Рисунок 1.4 - Схема переходной кривой

В качестве переходных кривых чаще всего используют радиоидальные спирали и реже —кубические параболы. У этих кривых кривизна К_х изменяется плавно, увеличиваясь пропорционально их длине l_x:

Столь же плавно изменяется центробежное ускорение, а следователь­но, и центробежные силы, благодаря чему снижается их отрицательное воздействие на пассажиров, путь и подвижной состав (рисунок 1.4, в).

Учитывая, что для конца переходной кривой 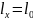и p_x = R, параметр переходной кривой определяется как:

Длину переходной кривой определяют по формуле:

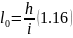
Во всех случаях длина переходной кривой не должна быть менее 20 м. Полученные по расчету значения длины переходной кривой округляют до значения, кратного 20 м, в большую сторону.

1.3.1 Разбивка переходной кривой

Элементы переходных кривых, необходимые для их разбивки на местности, находят в зависимости от способа разбивки. Различают следующие способы разбивки переходных кривых: способ сдвижки круговой кривой внутрь; способ введения дополнительных круговых кривых меньшего радиуса, чем радиус основной кривой; способ (Н.В. Харламова) смещения центра и изменения радиуса.

Р ассмотрим случай разбивки переходных кривых способом сдвижки. Этот способ заключается в следующем. Для разбивки кривых по координатам необходимо знать (рисунок 1.5) сдвижку р круговой кривой и расстояние m₀ от начала переходной кривой НПК до точки тангенса T₀. Но для этого, прежде всего, находят m— расстояние от начала переход­ной кривой до нового положения T, затем определяют сдвижку р, угол и все координаты кривой.

Рисунок 1.5 - Схема разбивки переходных кривых методом сдвижки круговой кривой внутрь

Из рисунка 1.5 видно, что

Тогда

Здесь x₀ и y₀ — координаты конца переходной кривой; угол ка­сательной к кривой в той же точке с положительным направлением оси абсцисс равен . В случае радиоидальной спирали

Для конца переходной кривой

Возможность устройства переходных кривых длиной l₀ при угле поворота линии определяется тем, чтобы длина круговой кривой была не меньше некоторого минимума L_min:

При этом L_min определяется условием размещения в ее пределах полной колесной базы экипажа. Можно принять L_min=0, если алгебраическая разность уклонов отводов возвышения наружного рельса примыкающих одна к другой переходных кривых не будет превышать макси­мально допустимого (но не использованного) уклона отвода возвыше­ния наружного рельса для каждой переходной кривой.

Проверяют возможность разбивки переходной кривой указанным способом по следующим условиям:

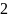. Определяют длину круговой кривой l_кк:

3. Сравнивают l_кк с минимально возможной длиной круговой кривой , определяемой длиной полной базы расчетного экипажа, которая принимается не менее 30 м. Если это условие не выполняется, то следует изменить радиус кривой.

Для разбивки переходной кривой необходимо определить ее вид.

Кубическую параболу применяют при условии:

Координаты такой кривой определяют по формуле:

Если условие (1.24) не выполняется, разбивка переходной кривой производится по радиоидальной спирали и координаты переходной кри­вой определяются по уравнениям:

Затем определяют основные размеры для разбивки переходной кривой. Расстояние т от начала переходной кривой до нового положения тангенсного столбика:

Расстояние m₀ от начала переходной кривой до первоначального положения тангенсного столбика:

Полная длина новой кривой (с переходными кривыми):

Суммированный тангенс новой кривой:

Суммарная биссектриса:

Домер:

Разбивку переходных и круговых кривых на местности производят геодезическими способами.