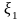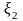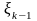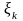- •Введение
- •Раздел 1. Виды, методы и задачи испытаний технических изделий Лекция1. Цели и задачи испытаний боеприпасов и их составных частей
- •Лекция 2. Опытно-теоретический метод оценки показателей эффективности
- •1.2.4.2. Метод эквивалентных возмущений
- •Раздел 2. Оценивание свойств изделий по результатам испытаний Лекция 3. Виды оценок. Методы получения точечных и интервальных оценок. Доверительный интервал и доверительная вероятность.
- •Основные этапы проверки статистических гипотез
- •2. Статистические гипотезы о дисперсиях
- •Лекция 4. Случайные процессы, их виды и параметры. Методы получения и обработки информации о случайных процессах
- •Раздел 3. Дисперсионный, корреляционный и регрессионный анализ результатов испытаний Лекция 5. Основные понятия статистического анализа. Задачи и виды статистического анализа.
- •Лекция 6. Дисперсионный и корреляционный анализ.
- •Лекция 7. Регрессионный анализ и планирование эксперимента.
- •Раздел 4. Принципы принятия статистических решений по результатам испытаний Лекция 8. Принцип Байеса. Постановка задачи. Вывод решающего правила.
- •1. Байесовский принцип
- •Лекция 9. Частные случаи принципа Баейса. Условие Зигерта-Котельникова. Принцип минимакса.
- •1) Метод минимального числа ошибочного решений:
- •2) Метод наибольшего правдоподобия.
- •2)Формирование решающего правила
1.2.4.2. Метод эквивалентных возмущений
Метод применим в том случае, когда нас
интересуют только математическое
ожидание оцениваемой характеристики
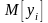 и дисперсия
и дисперсия
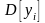 .
.
К достоинствам метода относятся следующие:
при числе случайных переменных менее 20-30 объем вычислительных работ существенно меньше по сравнению с предыдущим;
возможность проследить влияние каждого фактора
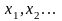 на случайные отклонения
на случайные отклонения
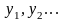 ;
;для задания при моделировании нет необходимости обращаться к специальным программам выработки случайных чисел.
К недостаткам метода следует отнести:
невозможность получить законы распределения оцениваемых при моделировании характеристик,
сложность оценки точности получаемых при моделировании характеристик.
Сущность метода кратко заключается в
следующем. Не снижая общности полученных
ниже результатов будем полагать
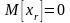 ,
,
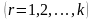 .
.
Будем полагать также, что существуют и известны моменты связи
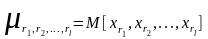 ,
,
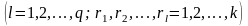 .
(1.4)
.
(1.4)
Решения системы (1.1) в общем случае можно представить в виде
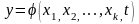 .
.
Предположим,
что функция
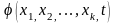 может быть разложена в ряд Маклорена
по переменным
может быть разложена в ряд Маклорена
по переменным
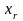 .
Ограничиваясь членом q
– й степени и опуская остаточный
член, получим
.
Ограничиваясь членом q
– й степени и опуская остаточный
член, получим
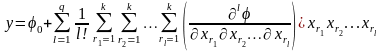 ,
(1.5)
,
(1.5)
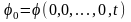 .
.
Подставим в выражение для
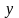 некоторые частные значения
некоторые частные значения
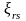 параметров
и проведем разложение функции
параметров
и проведем разложение функции
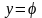 по этим параметрам. Аналогично (1.5)
получим
по этим параметрам. Аналогично (1.5)
получим
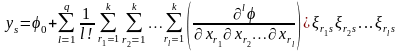 .
(1.6)
.
(1.6)
Величины
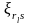 называются эквивалентными возмущениями.
Выберем
называются эквивалентными возмущениями.
Выберем
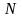 различных комбинаций эквивалентных
возмущений
различных комбинаций эквивалентных
возмущений
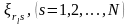
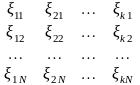
и подставим их в уравнение (1.6). Получим
уравнений вида (1.5). Умножая обе части
этих уравнений на некоторые, пока что
неопределенные коэффициенты
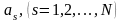 и суммируя полученные уравнения
почленно, найдем
и суммируя полученные уравнения
почленно, найдем
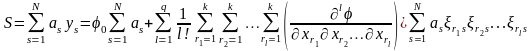 .(1.7)
.(1.7)
Математическое ожидание от (1.5) равно
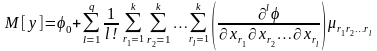 .
(1.8)
.
(1.8)
С
(1.9)
(1.10)
равнивая уравнения (1.7) и (1.8) можно сделать вывод, что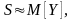 если
если
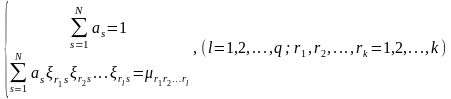 .
.
Выбирая в качестве величин
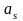 и
какое-либо действительное решение этой
системы, получим
и
какое-либо действительное решение этой
системы, получим
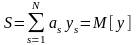 .
(1.11)
.
(1.11)
Величины
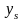 можно вычислить путем решения исходной
системы (1.1.) при подстановке в эту систему
соответствующих эквивалентных возмущений
вместо случайных переменных
.
можно вычислить путем решения исходной
системы (1.1.) при подстановке в эту систему
соответствующих эквивалентных возмущений
вместо случайных переменных
.
Аналогично можно показать, что
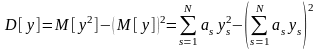 .
(1.12)
.
(1.12)
Точность полученных таким методом
вероятностных характеристик зависит
от вида уравнений (1.1) и степени
аппроксимирующего полинома
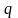 .
.
При q = 2 система уравнений (1.9), (1.10) запишется в виде:
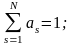 (1.13)
(1.13)
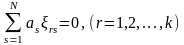 ;
(1.14)
;
(1.14)
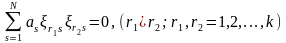 ;
(1.15)
;
(1.15)
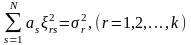 .
(1.16)
.
(1.16)
Число
различных
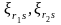 ,
при которых эта система уравнений имеет
действительное решение, в общем случае
определяется по формуле
,
при которых эта система уравнений имеет
действительное решение, в общем случае
определяется по формуле
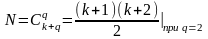
Специальным выбором можно добиться обращения в ноль многих коэффициентов и существенно сократить число решений системы (1.1).
Предлагается, например, представить величины в соответствии с таблицей 1.1. [ 2 ]
Таблица 1
s |
|
||||||
1 |
2 |
3 |
. . . |
k – 2 |
k – 1 |
k |
|
1 |
|
0 |
0 |
. . . |
0 |
0 |
0 |
2 |
0 |
|
0 |
. . . |
0 |
0 |
0 |
. . . |
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
||||||
k – 1 |
0 |
0 |
0 |
. . . |
0 |
|
0 |
k |
0 |
0 |
0 |
. . . |
0 |
0 |
|
k + 1 |
|
|
|
. . . |
|
|
|
k + 2 |
- |
- |
- |
. . . |
- |
- |
- |
Примечание.
Если
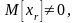 т.е.
т.е.
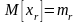 ,
то в таблице 1.1. вместо нулей необходимо
записать
,
то в таблице 1.1. вместо нулей необходимо
записать
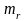 ,
а вместо
записать
+
,
вместо -
записать
–
.
В этом случае число решений системы
(1.1)
,
а вместо
записать
+
,
вместо -
записать
–
.
В этом случае число решений системы
(1.1)
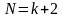 и первые два уравнения (1.13), (1.14) приводятся
к виду
и первые два уравнения (1.13), (1.14) приводятся
к виду
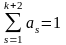 ;
(1.17)
;
(1.17)
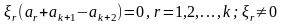 .
(1.18)
.
(1.18)
Суммируя
все
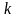 уравнений (1.18), найдем
уравнений (1.18), найдем
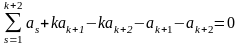 ,
,
или учитывая, что , получим
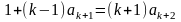 .
(1.19)
.
(1.19)
Уравнения (1.15), (1.16) в соответствии с таблицей 1.1 приводятся к виду:
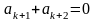 ;
(1.20)
;
(1.20)
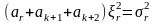 .
(1.21)
.
(1.21)
Отсюда имеем
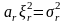 .
(1.22)
.
(1.22)
Из системы уравнений
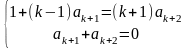
найдем
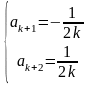 .
(1.23)
.
(1.23)
Подставив эти значения в уравнение (1.18), получим
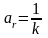 . (1.24)
. (1.24)
Подставив
значение
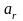 в (1.22), получим
в (1.22), получим
 . (1.25)
. (1.25)
Таким образом, если в системе уравнений
(1.1) содержится
некоррелированных переменных
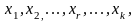 имеющих одинаковые законы распределения
с известными математическими ожиданиями
имеющих одинаковые законы распределения
с известными математическими ожиданиями
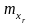 и среднеквадратическими отклонениями
и среднеквадратическими отклонениями
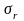 , то необходимо провести
, то необходимо провести
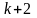 решения этой системы при подстановке
в нее вместо случайных переменных
эквивалентных возмущений, определенных
по формуле (1.25), в соответствии с
таблицей 1.1. В результате этих
решений будет получено
значения
решения этой системы при подстановке
в нее вместо случайных переменных
эквивалентных возмущений, определенных
по формуле (1.25), в соответствии с
таблицей 1.1. В результате этих
решений будет получено
значения
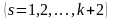 оцениваемых характеристик боеприпаса.
оцениваемых характеристик боеприпаса.
Имея эти значения , учитывая значения известных теперь коэффициентов из формул (1.23), (1.24) и используя уравнения (1.11), (1.12), можно вычислить математическое ожидание и дисперсию по формулам:
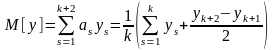 ;
(1.26)
;
(1.26)
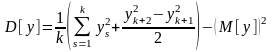 .
(1.27)
.
(1.27)
При
кубической аппроксимации функции
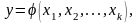 т.е. при
т.е. при
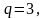 величины
величины
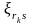 предлагается выбирать в соответствии
с таблицей 1.2 [ 2 ].
предлагается выбирать в соответствии
с таблицей 1.2 [ 2 ].
Таблица 1.2
s |
|
|||||
1 |
2 |
3 |
. . . |
k - 1 |
k |
|
1 |
|
0 |
0 |
. . . |
0 |
0 |
2 |
- |
0 |
0 |
. . . |
0 |
0 |
3 |
0 |
|
0 |
. . . |
0 |
0 |
4 |
0 |
- |
0 |
. . . |
0 |
0 |
. . . |
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
|||||
2k - 1 |
0 |
0 |
0 |
. . . |
0 |
|
2k |
0 |
0 |
0 |
. . . |
0 |
- |
В рассматриваемом случае к системе уравнений (1.13) – (1.16) добавятся уравнения вида
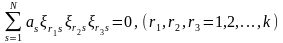 .
(1.28)
.
(1.28)
В соответствии с таблицей 1.2 будем иметь
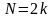 ;
(1.29)
;
(1.29)
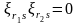 ,
при
,
при
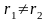 ;
(1.30)
;
(1.30)
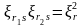 ,
при
,
при
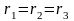 .
(1.31)
.
(1.31)
На основании равенства (1.30) заключаем, что все уравнения (1.15) при данном выборе величин удовлетворяются. Уравнения (1.14), (1.16) и (1.28) приводятся к виду.
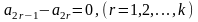 ;
(1.32)
;
(1.32)
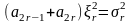 .
(1.33)
.
(1.33)
Выбирая
все
одинаковыми
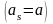 ,
удовлетворяем уравнениям (1.32), а из
уравнений (1.13) и (1.33) получаем
,
удовлетворяем уравнениям (1.32), а из
уравнений (1.13) и (1.33) получаем
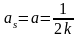 ;
(1.34)
;
(1.34)
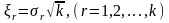 .
(1.35)
.
(1.35)
Если
подставить в систему уравнений (1.1)
вместо случайных переменных эквивалентные
возмущения
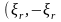 или
или
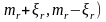 в соответствии с таблицей 1.2 и решить
эту систему, то получим
в соответствии с таблицей 1.2 и решить
эту систему, то получим
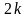 значений оцениваемой характеристики
вида
значений оцениваемой характеристики
вида
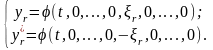 (1.36)
(1.36)
Математическое
ожидание
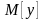 вычисляется по формуле
вычисляется по формуле
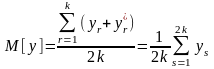 .
(1.37)
.
(1.37)
Дисперсия характеристики может быть определена по формуле
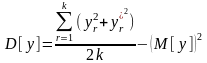 .
(1.38)
.
(1.38)
Если
в системе уравнений (1.1) содержится
только одна случайная переменная
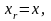 то формулы (1.37), (1.38) принимают вид
то формулы (1.37), (1.38) принимают вид
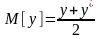 ;
;
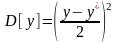 ,
,
т.е.
математическое ожидание равно полусумме
решений системы (1.1.), получающихся при
подстановке вместо
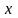 эквивалентных возмущений
эквивалентных возмущений
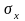 и –
,
а дисперсия равна квадрату полуразности
этих решений.
и –
,
а дисперсия равна квадрату полуразности
этих решений.
При
большом числе случайных переменных
(больших значений
)
может оказаться, что величины
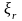 будут превосходить максимально возможные
значения параметров
.
При этом ошибка уравнения (1.5), обусловленная
отбрасыванием остаточного члена
разложения, может оказаться недопустимо
большой.
будут превосходить максимально возможные
значения параметров
.
При этом ошибка уравнения (1.5), обусловленная
отбрасыванием остаточного члена
разложения, может оказаться недопустимо
большой.
Однако можно легко получить формулы для определения математического ожидания и дисперсии характеристики , не требующие подстановки больших значений . Выберем , фигурирующие в таблице 1.2, пропорциональными соответствующим среднеквадратическим отклонениям :
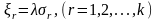 ,
(1.39)
,
(1.39)
где
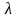 – постоянный коэффициент, не зависящий
от
– постоянный коэффициент, не зависящий
от
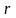 .
.
Можно получить для вычисления математического ожидания оцениваемой характеристики формулу [ 2 ]
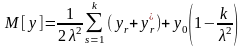 ,
(1.40)
,
(1.40)
где
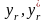 определяются уравнениями (1.36), а
определяются уравнениями (1.36), а
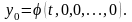 При
При
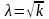 эта формула совпадает с (1.37).
эта формула совпадает с (1.37).
Интерполяционный метод
В отличие от метода эквивалентных возмущений интерполяционный метод разработан также и для расчета функций распределения вероятностей оцениваемых характеристик [ ], т.е. обладает такой же универсальностью, что и метод статистических испытаний (Метод Монте-Карло).
За счет оптимального выбора узлов интерполирования при одном и том же числе вариантов решений системы уравнений (1.1) интерполяционный метод дает более высокую точность, чем метод эквивалентных возмущений.
Имеются
таблицы [ ] оптимальных чисел
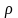 (числа Кристоффеля) и оптимальных
вариантов узлов интерполирования
(узлов Чебышева) для случайных величин,
имеющих равномерный, нормальный или
экспоненциальный законы распределения.
(числа Кристоффеля) и оптимальных
вариантов узлов интерполирования
(узлов Чебышева) для случайных величин,
имеющих равномерный, нормальный или
экспоненциальный законы распределения.
При практических расчетах необходимо преобразовать исходные случайные переменные к той или иной стандартной форме в зависимости от их законов распределения.
Если
случайная величина
имеет равномерный закон распределения
в промежутке
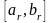 , то узлы типа Чебышева рассчитываются
по формуле
, то узлы типа Чебышева рассчитываются
по формуле
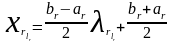 ,
(1.41)
,
(1.41)
где
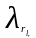 –
стандартные узлы Чебышева для равномерного
закона в промежутке [–1, 1].
–
стандартные узлы Чебышева для равномерного
закона в промежутке [–1, 1].
Если
случайная величина
имеет нормальный закон распределения
с параметрами
и
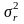 ,
то к стандартной форме она преобразуется
по формуле
,
то к стандартной форме она преобразуется
по формуле
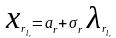 .
(1.42)
.
(1.42)
Стандартная
случайная величина имеет распределение
с параметрами
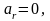
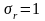 .
.
Случайная
величина, имеющая экспоненциальное
распределение с математическим
ожиданием
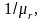 преобразуется к стандартной форме по
формуле
преобразуется к стандартной форме по
формуле
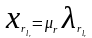 .
(1.43)
.
(1.43)
Математическое
ожидание
,
дисперсия
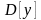 и
интегральный закон распределения
и
интегральный закон распределения
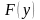 вычисляются по формулам:
вычисляются по формулам:
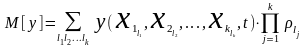 , (1.44)
, (1.44)
где
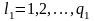 ;
;
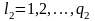 ;
…
;
…
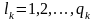 ;
;
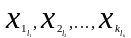 - различные варианты значений, полученные
путем приведения исходных случайных
величин к стандартному виду;
- различные варианты значений, полученные
путем приведения исходных случайных
величин к стандартному виду;
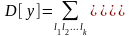 ; (1.45)
; (1.45)
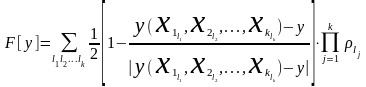 .
(1.46)
.
(1.46)
Общее число интегрирований системы уравнений (1.1) равно
 .
(1.47)
.
(1.47)
Значения
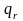 выбирают в соответствии с существующей
зависимостью оцениваемой характеристики
y от случайной переменной
.
Если эта зависимость близка к линейной,
то
=
1. При квадратической зависимости y
от
принимают
=
2 и т.д.
выбирают в соответствии с существующей
зависимостью оцениваемой характеристики
y от случайной переменной
.
Если эта зависимость близка к линейной,
то
=
1. При квадратической зависимости y
от
принимают
=
2 и т.д.
Пример
1.1. Пусть оцениваемая характеристика
y зависит от трех случайных переменных
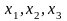 ,
распределенных по нормальному закону
с параметрами соответственно
,
распределенных по нормальному закону
с параметрами соответственно
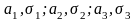 .
При этом также известно, что зависимость
от
.
При этом также известно, что зависимость
от
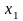 квадратическая (т.е.
квадратическая (т.е.
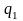 =
2 ), а от
=
2 ), а от
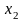 и
и
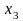 линейная (т.е.
линейная (т.е.
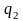 =
=
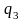 =
1). Общее число решений исходной зависимости
=
1). Общее число решений исходной зависимости
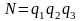 =
2.
=
2.
Из
таблиц [ ] находим значения оптимальных
чисел Кристоффеля
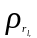 и
стандартных узлов Чебышева
,
и
стандартных узлов Чебышева
,
для
:
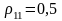 ;
;
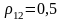 ;
;
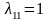 ;
;
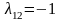 ;
;
для
:
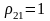 ;
;
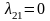 ;
;
для
:
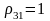 ;
;
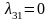 .
.
По формуле приведения (1.42) получим
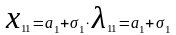 ;
;
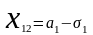 ;
;
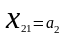 ;
;
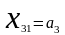 .
.
По формуле (1.44) получим
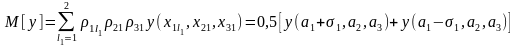 .
.
По формуле (1.45) найдем
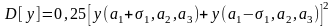 .
.