Бесконечно убывающая прогрессия

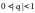
Бесконечно убывающей прогрессией (сокращенно БУГП) называется такая геометрическая прогрессия, у которой знаменатель по модулю меньше единицы ( ) и число членов которой бесконечно велико.

Т.к. по определению число членов в БУГП бесконечно велико и вследствие этого их пересчитать невозможно, то нельзя применять в такой прогрессии выражение «сумма членов». Вводится новый термин: сумма бесконечно убывающей геометрической прогрессии.

Термин «бесконечно убывающая» в приведённом определении следует понимать в том смысле, что убывают абсолютные величины членов прогрессии и .

Рассмотрим сумму « » первых членов прогрессии:

.

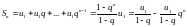Переходя к пределу, видим, что т.к. , то , при , тогда:

Получили формулу для суммы БУГП:

.

Задачи на бугп

Пример 1. Найти сумму членов геометрической прогрессии

Решение.

В данной прогрессии u₁=1, q=1/2; тогда .

Ответ: S = 2.

Пример 2. Сумма первых четырех членов б.у.г. прогрессии составляет 9/25 суммы всех ее членов. Определить первый член и знаменатель этой прогрессии, если второй член прогрессии равен 8, а первый положителен (u₁>0).

Решение.

Обозначим первый член прогрессии через u₁, а знаменатель q. Тогда по условию: ,

откуда находим

Ответ: 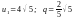Пример 3. Сумма членов б.у.г. прогрессии равна 56, а сумма квадратов ее членов равно 448. Найти эту прогрессию.

Решение.

По условию задачи:

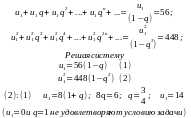
Ответ: .

§ 1.6 Неравенство Якоби-Бернулли.

Для , где справедливо неравенство:

(1)

Доказательство: 1. если , т.к. очевидно

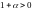2. то пусть теперь , тогда , т.к. .

, т.к. 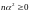. Тогда , согласно математической индукции и т.д.

§ 1.7 Неравенство Коши.

Среднее геометрическое нескольких положительных чисел не больше их среднего арифметического для и для имеем (1)

Доказательство: 1. при (1) принимает вид (доказывается из ).

2. предположим, что (1) справ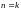едливо при . Докажем, что оно будет справедливо при , т.е.

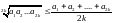
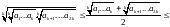
т.е. неравенство (1) справедливо для , где .

3. докажем, что из справедливости неравенства при следует справедливость при . Отсюда и покажем его справедливость для .

Пусть - некоторое неопределённое число, тогда 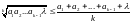. Выберем так, чтобы 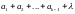делилось на , т.е. 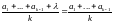, т.е. получим 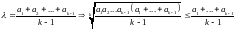или .

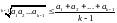Пусть теперь для будет иметь место то, что . Но по доказательству в пункте (2) для него неравенство справедливо. Если же , то найдётся такое s, чтобы для , что будет выполнено условие (2) и тогда на основании основных пунктов (2) и (3) утверждение (1) будет верно для .

Или несколько изменённый вид :

§ 1.8 Аксиома полноты действительных чисел .

Для любых двух непустых множеств действительных чисел X и Y, обладающих свойством, что каждый элемент не превосходит , что имеет место неравенство:

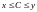, справедливо для всех и , т.е. .

§ 1.9 Бином Ньютона.

(Сумму двух слагаемых, называют двучленами или биномами).

Для справедливо разложение (*)

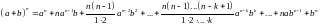Введём некоторые обозначения, которые позволят нам сократить формулу (*):

1. 

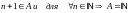
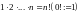
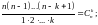2. причем и

Или 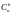-число сочетаний из «n» по «k»,С –первая буква французского слова combinasion-сочетание.

,

тогда формула (*), с учётом обозначений, будет иметь вид:

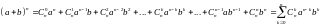, где

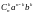- член разложения выражения (*), а числа - коэффициенты разложения, или биномиальные коэффициенты.

Доказательство: пусть имеем некоторое множество , тогда для чисел этого множества выполняется формула бинома Ньютона:

1. 

2. пусть , т.е. на этом множестве выполнена формула (*), т.е. .

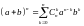Докажем, что на этом множестве выполняется формула (*) для всех чисел. Тем самым мы покажем, что множество -чисел будет являться подмножеством множества А. Для этого возьмём выражение (*) для :

Биномиальные коэффициенты обладают следующими свойствами:

= ,

тогда

, т.к.

, тем самым мы доказали, что формула бином Ньютона истинна.

Формула (*) названа в честь английского математика и физика И.Ньютона (1643-1727). Иногда формулу (*) называют формулой Ньютона. Он её указал в 1676 году, хотя строгое обоснование её дал Абель в 1826г.