Арифметическая прогрессия

Последовательность, у которой каждый член, начиная со второго, получается из предыдущего прибавлением одного и того же числа или одного и того же выражения, называемого разностью прогрессии, носит название арифметической прогрессии. Условимся обозначать её символом _.

Таким образом, арифметическая ( ) прогрессия – это заданная рекуррентно, т.е. , где , - разность . Обыкновенно её записывают в виде

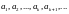
Пример 1.

Написать несколько первых членов , если и

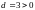
Решение:

По формуле находим:

; ;

; ;

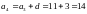Имеем

Пример 2:

Написать несколько первых членов , если и .

Решение:

С помощью той же формулы определяем:

; ;

; ;

Т.о.,

При прогрессия называется возрастающей, а при прогрессия называется убывающей.

Случай , все члены прогрессии равны первому члену 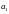. не будет ни возрастать, ни убывать. Этот случай не рассматривается.

Из определения , что для 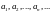верно:

1. 

2. Любой член , кроме первого, равен среднему арифметическому двух соседних с ним членов, т.е. , где

Доказательство:

По определению имеем:

+

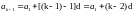
ч.т.д.

3. Выведем формулу общего члена .

По определению имеем:

Складывая « » равенств, получаем: .

Отнимая от обеих частей последнего равенства сумму , имеем

( )

Т.е. член прогрессии равен первому члену, сложенному с произведением разности прогрессии на число членов предшествующих определяемому.

Докажем формулу ( ) методом математической индукции:

1. При , , равенство справедливо.

2. Пусть равенство справедливо при , т.е.

3. Докажем, что из этого предположения справедливость и про , т.е. что

По определению , используя предположение, получаем 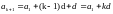. На основании принципа мат. индукции равенство ( ) справедливо.

4. Сумма двух симметричных по отношению центра конечной прогрессии, есть величина постоянная для этой прогрессии, равная сумме крайних её членов.

Пусть дана :

Стрелками показаны симметричные (равноудалённые) члены.

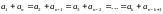
Мы видим, что у двух равноудалённых членов сумма нижних значков (индексов), указывающих их порядковые номера от начала, всегда равняется (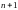 ), теперь наше утверждение можем записать в алгебраической форме.

Докажем: .

+

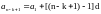
ч.т.д.

5. Формула для суммы « » членов прогрессии.

Пусть дана прогрессия .

Обозначая сумму « » первых её членов , запишем два равенства:

+

Учитывая равенство ,

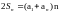
Имеем: , т.к. , то

, т.е. для прогрессии сумма есть квадратичная функция от переменной « ».

6. Методом математической индукции доказать формулу суммы « » первых членов прогрессии.

( )

Доказательство:

1. При имеем , т.е. высказывание Р(1) верно.

2. Предположим, что - истинно при .

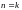3. Покажем, что тогда .

Действительно, имеем .

( )

Исключим член . По формуле общего члена прогрессии имеем , т.к. , то 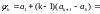(или после преобразования)

Подставляя найденное выражение в формулу ( ) получаем:

.

Этот результат показывает, что находится по формуле ( ), если положить , т.е. формула ( ) верна при , и из её истинности при , что она истина при , следовательно, она верна при всех .

При доказательстве справедливости этой формулы для была использована формула общего члена прогрессии, справедливость которой для была обоснована ранее.

Существует пять величин, характеризующие прогрессию: ,

а соотношений между ними только два:

• .

Поэтому задачи на должны содержать три известных величины из пяти.

7. Запишем ещё одну важную формулу, которая даёт возможность решать целый класс задач на . Запишем два члена прогрессии и вычтем их друг из друга:

.

_{Отсюда разность} .

Т.е. разность прогрессии равняется разности её двух членов, делённой на разность их номеров.