5.2. Метод жордановых преобразований
Рассмотрим систему, состоящую из 3-х уравнений с тремя неизвестными
.
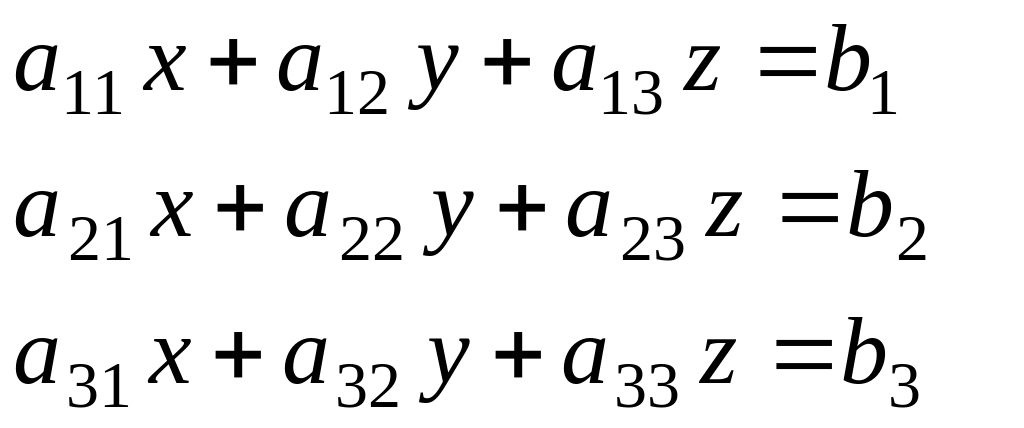Данную систему можно представить в виде таблицы:
(1)
Выбираем любой отличный от нуля коэффициент . Например, .
Жордановым
преобразованием системы с ведущим
элементом
называется совокупность следующих
преобразований:
1) умножение
i-ой строки таблицы (1) на число
(2-й строки на
)
-
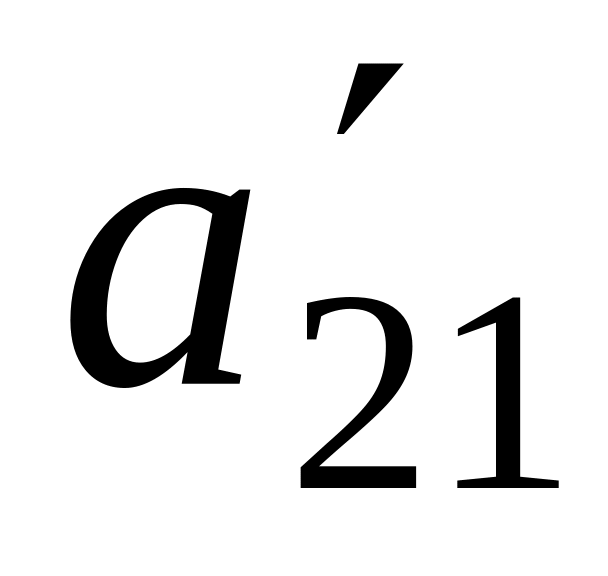
1
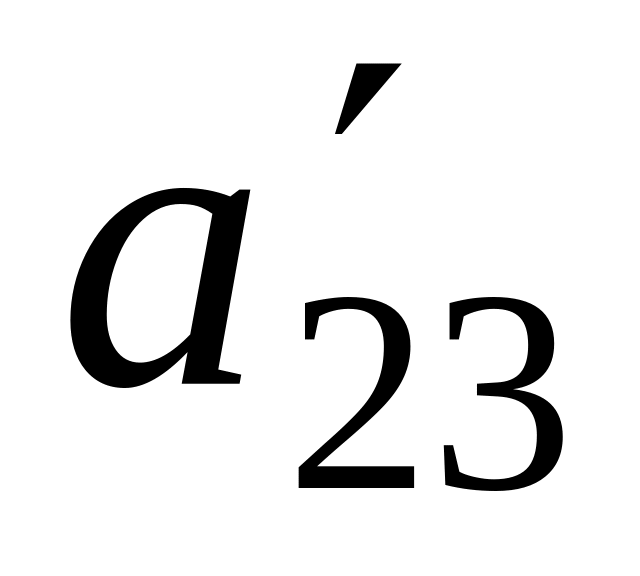
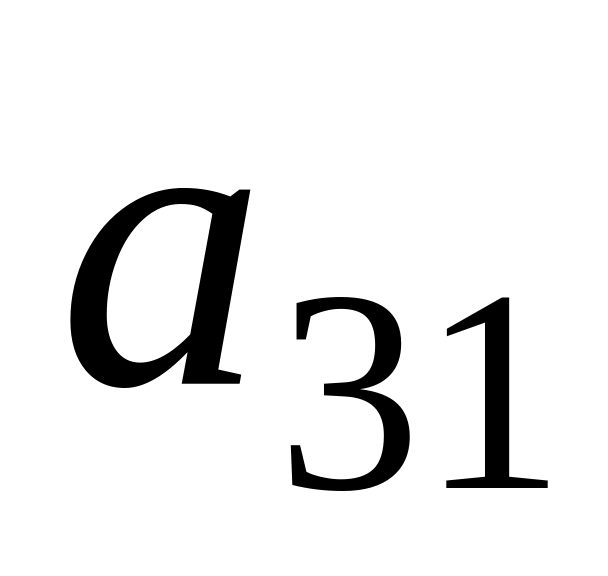
(2)
2) прибавление
в 1-ой строке таблицы ее i-й строки (2-ой
строки), умноженной на
,
к третьей строке ее i-й строки (2-ой
строки), умноженной на
,
и т. д.
После этих преобразований система уравнений примет вид:
-
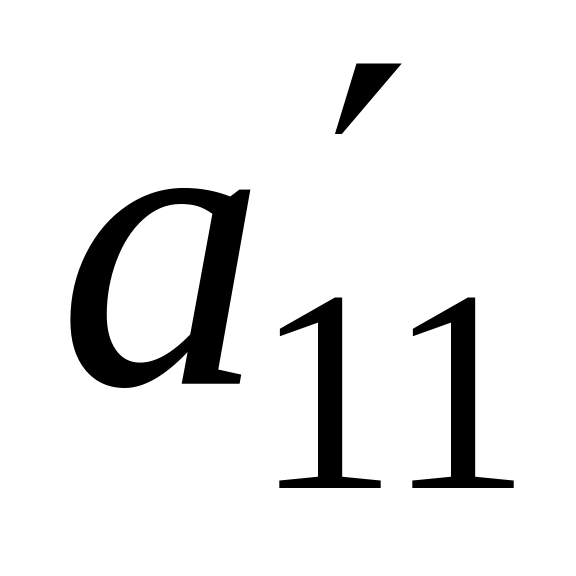
0
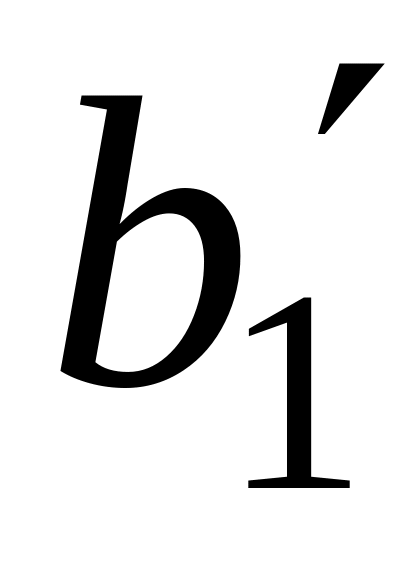
1
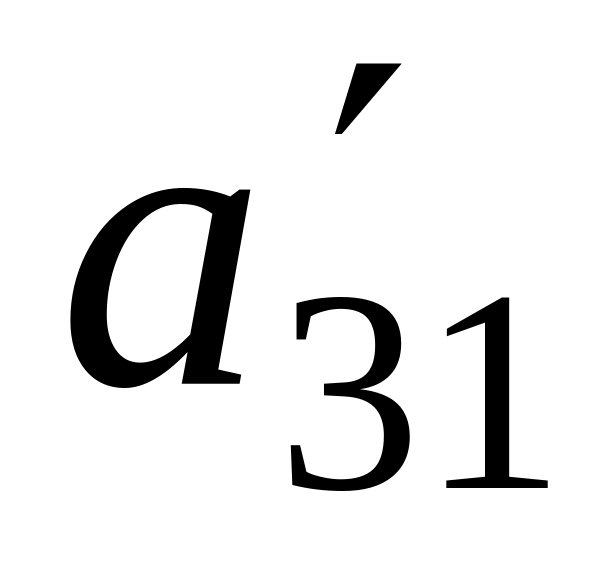
0
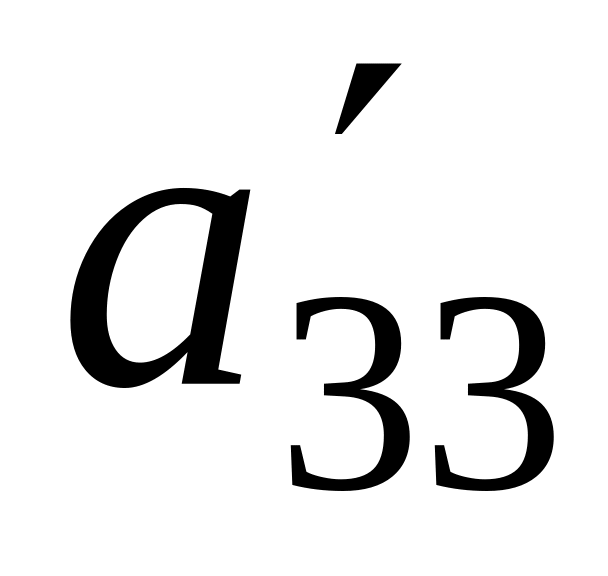
(3)
В результате Жорданова преобразования с ведущим элементом получаем систему (3), у которой неизвестное является разрешенным.
Пример. Решить систему линейных уравнений, используя Жордановы преобразования
.
Запишем систему в виде таблицы
|
|
|
|
|
|
|
|
|
|
|
-3 |
1 |
3 |
|
2 |
-3 |
1 |
3 |
|
1 |
0 |
-1 |
3 |
|
3 |
-3 |
0 |
6 |
|
|
1 |
0 |
8 |
|
3 |
1 |
0 |
8 |
|
0 |
13 |
-3 |
8 |
|
+6 |
4 |
0 |
17 |
|
2
3
|
|
|
|
|
|
|
|
|
|
|
0 |
-1 |
1 |
-1 |
|
0 |
0 |
1 |
|
|
1 |
-1 |
0 |
2 |
|
1 |
0 |
0 |
|
|
0 |
4 |
0 |
2 |
|
0 |
1 |
0 |
|
|
0 |
10 |
0 |
5 |
|
0 |
0 |
0 |
0 |
Переходим к общему
решению.
;
;
.
Ответ: ; ; .