2. Векторы. Операции над ними
Элементы пространства
R
называются n-мерными
векторами.
Обозначаем:
=(х
,х
,…х
),
где
(i=
)
называются координаторами вектора
,
n
– размерность
вектора
.
Размерность можно обозначить так dim = n.
Чтобы умножить
вектор
= (х
,
х
,…х
)
на скаляр
k, надо
каждую координату вектора
умножить на скаляр k.
k = (k х , k х ,… k х ).
Чтобы сложить
два n-мерных
вектора
=(х
,
х
,…х
)
и
=
(у
,у
,…,у
),
надо сложить соответствующие координаты.
+ = (х + у , х + у , … х + у ).
Скалярным произведением векторов и называется число, находимое по формуле:
=
х
у
+
х
у
+
… +х
у
=
х
у
.
Свойства умножения вектора на скаляр и сложения векторов
1.
+
=
+
2. (
+
)
+
=
+ (
+
)
3. k ( + ) = k + k 4. (k +k ) = k + k
5. (k k ) = ( k ) k = (k ) k
Свойства скалярного произведения векторов
=
;
2.
(
+
)
=
+
;
3. k(
)=(k
)
=
(k
)
Длина вектора = (x ,x ,…,x ) определяется формулой
Расстояние между п-мерными точками (точками в R ) A(а ,а ,…,а ) и B(b , b ,…,b ) определяется формулой
Косинус угла между п-мерными векторами и находится по формуле:
,
где 0
φ
π.
Примеры решения задач
Пример 1.
Дана система векторов в R
:
=
(1, 2, 4);
=
(0, 3, – 1);
=
(3, 1, 2);
= (– 2, 0, – 1).
1. Найти линейные комбинации этих векторов.
2 – + – ; б) + 2 – 3 + ; в) – – – – .
Решение:
2
.
.–
.
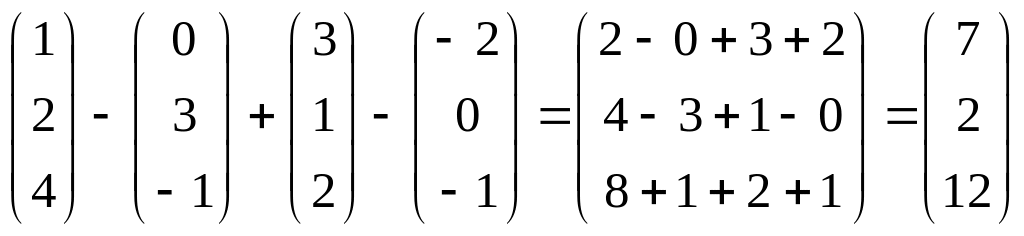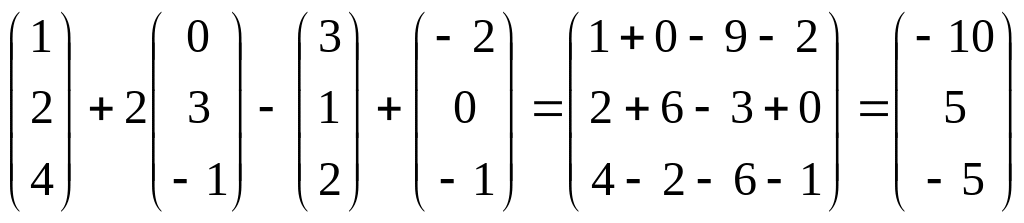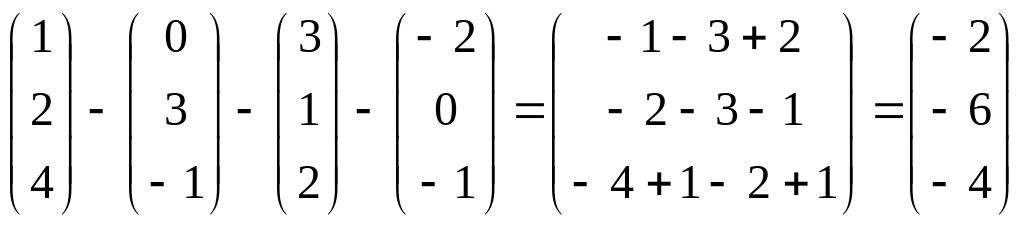2. Найти значение выражения: 2( + ) – 3( – 4 ).
Решение:
2(
+
)
– 3(
–
4
)
= 2
+ 2
– 3
+
12
= 2
–
+
12
=
=2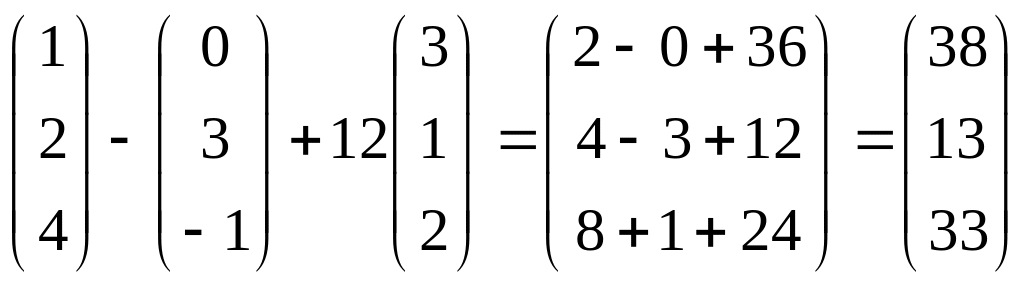
.
3. Найти скалярные произведения:
, , , , , .
Решение:
= 1 0 + 2 3 + 4 (–1) = 6 –4 = 2;
= 1 3+2 1+4 2 = 3 + 2 + 8 = 13;
= 1 (–2) + 2 0 + 4 (–1) = –2 –4 = –6;
= 0 3 + 3 1+ (–1) 2 = 3 –2 = 1;
= 3 (–2) + 3 0 +(–1) ( –1) = 1 ;
= 3 (–2) + 1 0 + 2 (–1) = –6 –2 = –8.
4. Найти длины
векторов
,
,
,
с точностью до 0,001.
Решение:
=
=
=
= 4,583.
=
=
=
=
3,162.
=
=
=
=
3,742.
=
=
=
=
2,236.
5. Найти значение выражения: (2 + ) + 2 .
Решение: решим по действиям
2 = (0, 6, – 2).
(2 + ) = (3, 7, 0).
(2 + ) = 1 3 + 2 7 +4 0 = 3 + 14 = 17.
= = 13.
17 + 13 = 30.
Пример 2. Даны
точки в пространстве R
:
А (1, 2, 1, 3, 2), В (1, 4, 1, – 1, 0), С (1, 2, 1, 1, 1).
Найти расстояния
с
точностью до 0,0001.
Решение: Согласно формуле
=
=
=
=
=
4,9000.
Заметим, что
.
=
=
=
=
=
3,0000.
=
=
=
=
=2,2361.
Пример 3.
Найти вектор
из уравнения
а)
,
если
= (5, – 8, – 1, 2),
= (2, – 1, 4, – 3),
=
(– 3, 2, – 5, 4).
б) 3
,
если
(2,
5, 1, 3),
(10,
1, 5, 10),
(4,
1, -1, 1).
Решение: а)
+
+
+
=
,
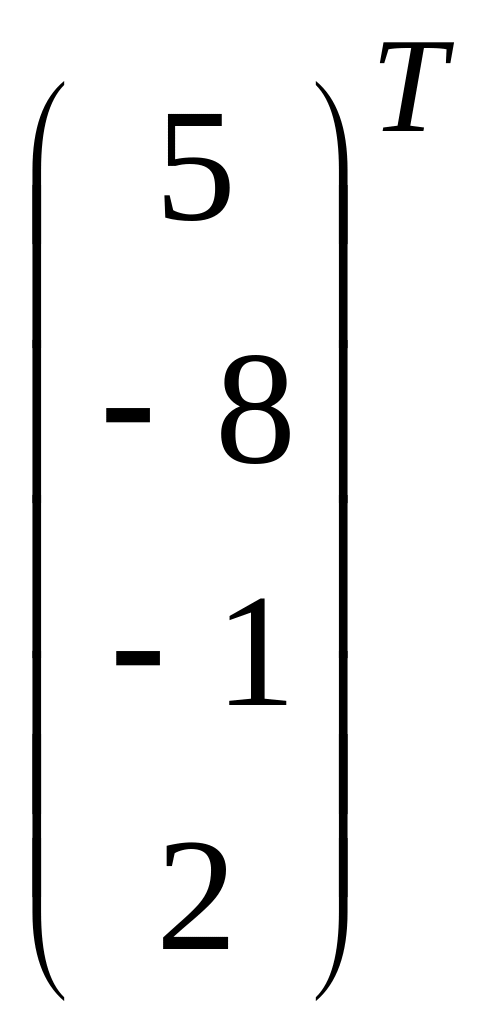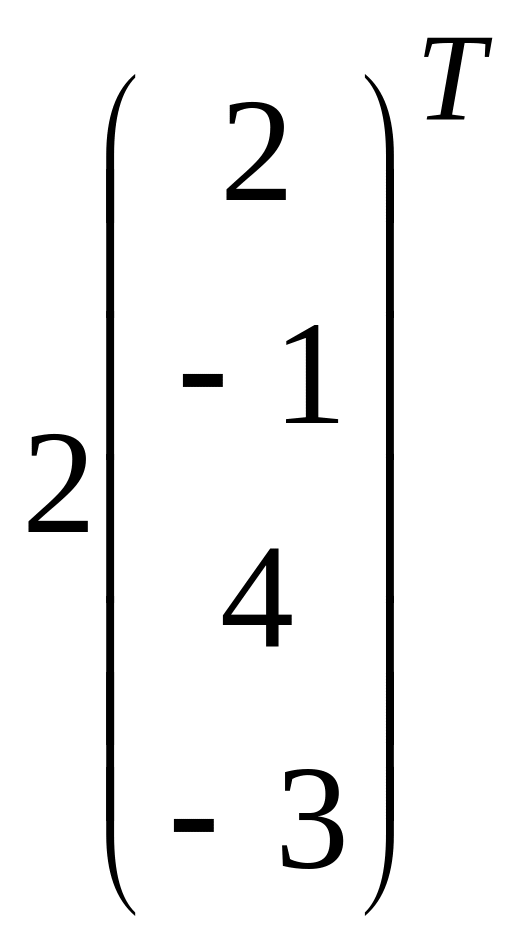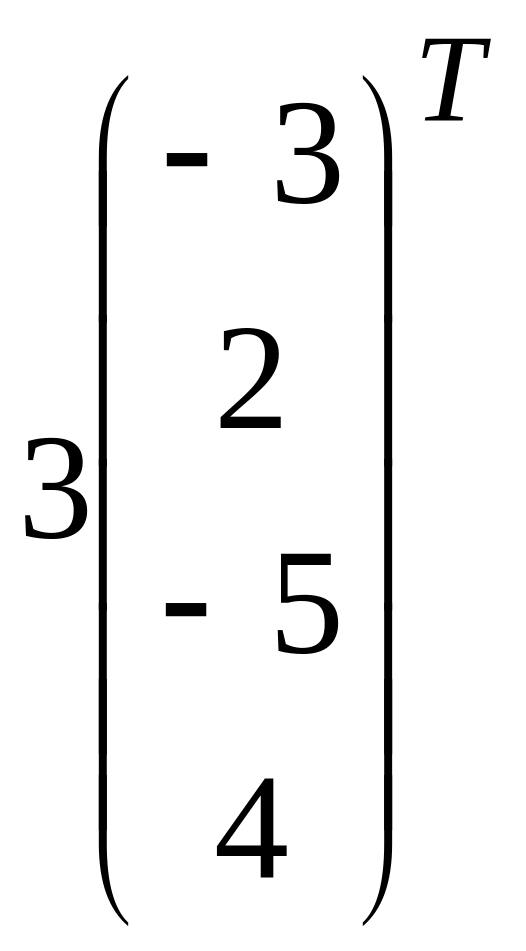откуда
5 + 4 – 9 = – 4 х 0 = – х х = 0
– 8 – 2 + 6= – 4х – 4 = – 4х х = 1
– 1 + 8 – 15= – 4х
– 8 = – 4х
х
=
2
2 – 6 + 12= – 4х
8 = – 4х
х
=
–2
Ответ: = (0, 1, 2, -2).
Решение: б) Преобразуем выражение (отдельно каждую скобку):
3
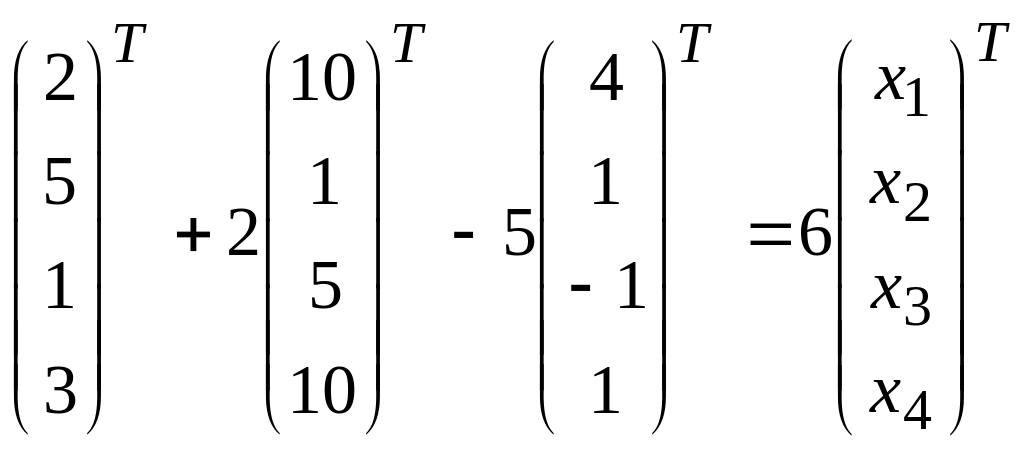
6 + 20 – 20 = 6х 6 = 6 х х = 1
15 + 2 – 5 = 6х 12 = 6 х х = 2
3 + 10 + 5 = 6х 18 = 6 х х = 3
9 + 20 – 5 = 6 х 24 = 6 х х = 4
Ответ: = (1, 2, 3, 4).
СЕМИНАР 2.
N-МЕРНЫЕ ВЕКТОРЫ. ОПЕРАЦИИ НАД НИМИ.
СВОЙСТВА ОПЕРАЦИЙ НАД ВЕКТОРАМИ