Решение основной задачи динамики

Основное уравнение динамики частицы:

это дифференциальное уравнение движения частицы, его решение - основная задача динамики материальной точки.

Решение уравнения проводят одним из трех

способов:

1)в векторной форме,

2)в координатах или 3)в проекциях на касательную и нормаль к

траектории в данной точке.

21

Знак проекции результирующей силы определяет

и знак проекции вектора ускорения.

22

Задача 1.

Брусок массы т скользит вниз по наклонной плоскости, составляющей угол α с горизонтом. Коэффициент трения равен μ. Необходимо определить ускорение бруска относительно плоскости, которая может рассматриваться как инерциальная система отсчета.

Скольжение частицы по наклонной плоскости

23

Изобразим все силы, действующие на брусок:

противоположную движению бруска.

Выберем ось х, как показано на рисунке, указав её положительное направление.

Составление уравнений:

слева - произведение массы т бруска на проекцию его ускорения ах и

справа - проекции всех сил на ось x:

24

В данном случае ,

следовательно

Так как тело движется только вдоль оси х, то это значит, что сумма проекций всех сил на любое перпендикулярное оси х направление равна нулю.

Выбрав в качестве такого направления ось у, c учетом закона Кулона-Амонтона, связывающего силу трения и нормальной реакции, получим при условии, что началось скольжение тела:

25

В итоге

Если правая часть этого уравнения окажется положительной, то и а это значит, что направлен вниз по наклонной плоскости. Если же наоборот, то это значит, что сделанное предположение о начале скольжения неверно, и тело будет удерживаться силой трения в покое на наклонной плоскости.

26

Проектируя обе части уравнения на подвижные векторы тангенциального и нормального 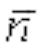ускорений) и используя полученные ранее для них выражения, запишем:

и.

Этими уравнениями удобно пользоваться, если заранее известна траектория материальной точки.

27

Задача 2.

Небольшое тело А начинает соскальзывать с вершины гладкой сферы радиуса r. Определим скорость тела в момент отрыва от поверхности сферы. Изобразим силы, действующие на тело А :

•сила тяжести

•нормальная сила реакции

Запишем уравнения движения в проекциях на направления векторов и :

28

Преобразуем первое уравнение к виду, удобному для интегрирования. Воспользовавшись тем, что

где - элементарный путь тела за промежуток времени ; перепишем первое уравнение в виде :

Проинтегрируем левую часть этого выражения от 0 до v, правую- от 0 до , и получим

29

Отметим, что если правую и левую части полученного уравнения

умножить на массу тела А и разделить на 2, то мы получим закон сохранения энергии – кинетическая энергия равна потенциальной.

При отрыве тела от поверхности , поэтому второе исходное уравнение принимает вид

Исключив из последних двух равенств, получим А разделив одно на другое

= 2/3 .

30