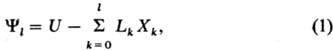Шпаргалка По Физике (Штеренберг А. М.) / 40.Уравнение политропы

40.Уравнение политропы. Коэффициент Пуассона. Термодинамические потенциалы.

Политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость c газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими.

Для идеального газа уравнение политропы может быть записано в виде:

pVⁿ = const, где величина n= C-C_p / C-C_v называется показателем политропы.

В зависимости от процесса можно определить значение n:

1. Изотермический процесс: n = 1, так как PV¹ = const, значит PV = const, значит T = const.

2. Изобарный процесс: n = 0, так как PV⁰ = P = const.

3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона.

4. Изохорный процесс: , так как , значит P₁ / P₂ = (V₂ / V₁)ⁿ, значит V₂ / V₁ = (P₁ / P₂)^{(1 / n)}, значит, чтобы P₁ и P₂ обратились в 1, n должна быть бесконечность.

C=Cp – изобарный

C=Cv – изохорный

C=1 - изотерма

C=0 – адиабата

Коэффициент Пуассона характеризует упругие свойства материала. При приложении к телу растягивающего усилия оно начинает удлиняться (то есть длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз изменяется поперечное сечение деформируемого тела при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона = 0, для абсолютно упругого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5. (Измеряется в относительных единицах (мм/мм, м/м))

,

где ν — коэффициент Пуассона, — деформация в поперечном направлении (отрицательный для осевого растяжения, положительный для осевого сжатия), — продольная деформация (положительный для осевого растяжения, отрицательный для осевого сжатия

Термодинамические потенциалы (термодинамические функции) — функции основных макроскопических параметров (температура, давление, энтропия и т. д.) термодинамической системы, характеризующие её состояние:

внутренняя энергия, энтальпия, свободная энергия Гельмгольца, потенциал Гиббса, большой термодинамический потенциал

Общая формула для термодинамических потенциалов: