Министерство образования Российской Федерации

Московский Государственный Университет Печати

Факультет полиграфической технологии

Дисциплина: Математика

Курсовая работа по теме:

“Статистические методы обработки

экспериментальных данных”

Выполнила: студентка Синева Е.Д.

курс 2

группа ДТуп 2-1

форма обучения очная

Номер зачетной книжки ДД 008

Вариант № 21

Допущено к защите

Дата защиты

Результат защиты

Подпись преподавателя

Москва – 2010 год

Вариант №21

Исходные данные.

Интервалы	1,5; 3,5	3,5; 5,5	5,5; 7,5	7,5; 9,5	9,5; 11,5	11,5; 13,5	13,5; 15,5	15,5; 17,5	17,5; 19,5	19,5; 21,5	21,5; 23,5
Частоты,	4	7	16	23	25	30	24	21	18	8	4

1. Построение интервального и точечного статистических распределений результатов наблюдений. Построение полигона и гистограммы относительных частот.

- порядковый номер;

- интервал разбиения;

- середина интервала;

- частота;

- относительная частота;

- плотность относительной частоты;

Объем выборки: ;

Длина интервала разбиения (шаг):

1	1,5;3,5	2,5	4	0,02	0,01
2	3,5;5,5	4,5	7	0,04	0,02
3	5,5;7,5	6,5	16	0,09	0,04
4	7,5;9,5	8,5	23	0,13	0,06
5	9,5;11,5	10,5	25	0,14	0,07
6	11,5;13,5	12,5	30	0,17	0,08
7	13,5;15,5	14,5	24	0,13	0,07
8	15,5;17,5	16,5	21	0,12	0,06
9	17,5;19,5	18,5	18	0,1	0,05
10	19,5;21,5	20,5	8	0,04	0,02
11	21,5;23,5	22,5	4	0,02	0,01
		Σ	180	1

Объём выборки:

n==180,

w_i= ;

контроль: =1

Длина интервала

разбиения (шаг):

h= 2

H_i=

Статистическим распределением называется соответствие между результатами наблюдений (измерений) и их частотами и относительными частотами. Интервальное распределение – это наборы троек (I_i ; n_i ; w_i) для всех номеров i, а точечное – наборы троек (x_i ; n_{i ;} w_i). Таким образом, в таблице имеются оба – и интервальное, и точечное - статистическое распределения.

Далее, строим полигон и гистограмму относительных частот.

Полигон относительных частот – ломаная, отрезки которой последовательно (в порядке возрастания x_i) соединяют точки (x_i ; w_i). Гистограмма относительных частот – фигура, которая строится следующим образом: на каждом интервале I_i, как на основании, строится прямоугольник, площадь которого равна относительной частоте w_i; отсюда следует, что высота этого прямоугольника равна H_i = ^w_i/h – плотности относительной частоты. Полигон и гистограмма являются формами графического изображения статистического распределения.

2. Нахождение точечных оценок математического ожидания и дисперсии.

В качестве точечных оценок числовых характеристик изучаемой случайной величины используются:

• для математического ожидания

= (выборочная средняя),

• для дисперсии

s² = (исправленная выборочная),

где n – объём выборки, n_i – частота значения x_i .

Таким образом, в статистических расчетах используют приближенные равенства

MX  , DX  s² .

Нахождение точечных оценок математического ожидания и дисперсии по данным варианта осуществим с помощью расчетной таблицы.

1	2,5	4	10	404,46
2	4,5	7	31,5	454,24
3	6,5	16	104	586,72
4	8,5	23	195,5	378,29
5	10,5	25	262,5	105,63
6	12,5	30	375	0,09
7	14,5	24	348	90,74
8	16,5	21	346,5	326,73
9	18,5	18	333	636,06
10	20,5	8	164	504,91
11	22,5	4	90	395,57
	Σ	180	2260	3883,44

12,56

В статистических расчетах используют приближенные неравенства:

3. Выдвижение гипотезы о распределении случайной величины.

При выдвижении гипотезы (предположения) о законе распределения изучаемой случайной величины мы опираемся лишь на внешний вид статистического распределения. Т.е. будем руководствоваться тем, что профиль графика плотности теоретического распределения должен соответствовать профилю гистограммы: если середины верхних сторон прямоугольников, образующих гистограмму, соединить плавной кривой, то эта линия представляет в первом приближении график плотности распределения вероятностей.

Итак, изобразим график и выпишем формулу плотности нормального (или гауссовского) распределения с параметрами а и , -  а  + ,

Сравнение построенной гистограммы и графика плотности распределения приводит к следующему заключению о предполагаемом (теоретическом) законе распределения в рассматриваемом варианте исходных данных:

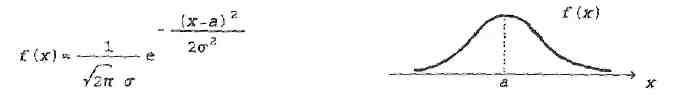
Вариант 21 – нормальное (или гауссовское распределение).

4. Построение графика теоретической плотности распределения.

Чтобы выписать плотность теоретического (предполагаемого) распределения, нужно определить значения параметров и а и подставить их в соответствующую формулу. Все параметры тесно связаны с числовыми характеристиками случайной величины, т.е.

MX = а ,

DX =

Поскольку значения математического ожидания и дисперсии неизвестны, то их заменяют соответствующими точечными оценками, т.е. используют (уже упомянутые ранее) приближенные равенства MX  , DX  s² , что позволяет найти значения параметров распределения.

По исходным данным была выдвинута гипотеза о нормальном распределении изучаемой случайной величины. Найдем параметры этого распределения:

_

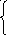
x = а, 12,56=а, а=12,56,

s²=21,7= σ² σ=4,6

Следовательно, плотность предполагаемого распределения задается формулой

F(x)= [1/(7.54*√2π)]*e^[-(x-12.56)^2/2*(4,6)^2)]=0.053*e^(21,7/((x-12,56)^2))

Теперь необходимо вычислить значения f(x_i) плотности f (x) при x=x_i (в серединах интервалов) Для этого воспользуемся следующей схемой:

значения фунцкии

при u=u_i находятся, например, с помощью таблицы, имеющейся в любом учебнике или задачнике по теории вероятностей и математической статистике.

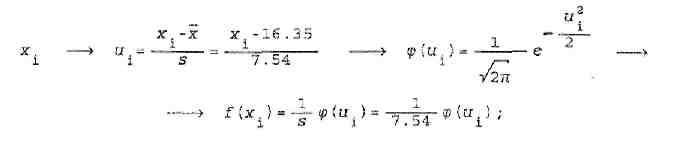
2,5	-2,16	0,039	0,008
4,5	-1,73	0,089	0,019
6,5	-1,3	0,171	0,037
8,5	-0,87	0,273	0,059
10,5	-0,44	0,362	0,078
12,5	-0,01	0,399	0,086
14,5	0,42	0,366	0,079
16,5	0,85	0,279	0,06
18,5	1,28	0,177	0,038
20,5	1,71	0,093	0,02
22,5	2,14	0,041	0,009

Далее, на одном чертеже строим гистограмму и график теоретической плотности распределения: гистограмма была построена ранее, а для получения графика плотности наносим точки с координатами (x_i ; f(x_i))и соединяем их плавной кривой.

5. Проверка гипотезы о распределение с помощью критерия согласия Пирсона.

Ранее была выдвинута гипотеза о законе распределения рассматриваемой случайной величины. Сопоставление статистического распределения (гистограмма) и предполагаемого теоретического (графика плотности) показывает наличие некоторых расхождений между ними. Поэтому возникает естественный вопрос: чем объясняются эти несовпадения? Ответить на него можно двояко:

1. Указанные расхождения несущественны и вызваны ограниченным количеством наблюдений и случайными факторами – случайностью результата единичного наблюдения, способа группировки данных и т.п. В этом случае выдвинутая гипотеза о распределении считается правдоподобной и принимается как не противоречащая опытным данным.

2. Указанные расхождения являются существенными (неслучайными) и связаны с тем, что действительное распределение случайной величины отличается от предполагаемого. В этом случае выдвинутая гипотеза о распределении отвергается как плохо согласующаяся данными наблюдений.

Для выбора первого или второго варианта ответа и служат так называемые критерии согласия. Словари толкуют слово критерий (от греч. kriterion – средство для суждения) как признак, на основании которого производится оценка, определение и классификация чего-либо.

Существуют различные критерии согласия: К. Пирсона, А.Н. Колмогорова, Н.В. Смирнова, В.И. Романовского и другие. Мы рассмотрим лишь один из них – критерий Пирсона, называемый также критерием ² («хи - квадрат»). (К. Пирсон (1857 - 1936) – английский математик, биолог, философ – позитивист.)

Критерий Пирсона выгодно отличается от остальных, во – первых, применимостью к любым (дискретным, непрерывным) распределениям и, во – вторых, простотой вычислительного алгоритма.

Правило проверки статистических гипотез с помощью критерия Пирсона будет объяснено на примерах.