3. Инвариантность уравнений релятивистской и классической механик при наличии сопротивления среды

Итак, в предыдущем разделе был сформулирован принцип пространственного дуализма, который позволяет коренным об- разом изменить наши представления о физической природе и свойствах пространства, как об одном из самых сложных и мало- изученных физических объектов. Сущность принципа простран- ственного дуализма заключается в том, что наблюдаемые физи- ческие законы можно представлять в виде математических моде- лей и формул, не учитывая специально уровня энергии самого пространства, рассматривая его как абсолютную пустоту (СТО), или как упругую энергоемкую среду (теория УКС).

Однако, рассматривая пространство или абсолютную пусто- ту, его упругие свойства заранее учитываются определенными константами (электрической и магнитной проницаемостью), в том числе главной — константой скорости света. С одной сторо- ны, это, казалось бы, упрощает описание физических законов, но с другой — искажает реальную картину физического мира. Принимая пространство за абсолютную пустоту, мы заранее ста- вим себя в невыгодное положение, пытаясь придать пустому про- странству определенные физические свойства. Наглядный при- мер тому — это общая теория относительности (ОТО), первона- чально задуманная Эйнштейном как общая теория поля, но не- состоявшаяся даже в руках гения, поскольку неправильно были выбраны исходные положения. Первым этапом общей теории предусматривалось объединение гравитации и электромагнетиз- ма. С этой задачей смогла справится теория УКС, положив в ос- нову пространства электромагнитную энергоемкую структуру [1]. Будущее энергетики, транспорта и связи зависит от того, насколько глубоки будут наши знания о структуре пространства. Чтобы по- бедить гравитацию, необходимо полностью отказаться от кон-

цепции пустого пространства, как несостоятельной.

Теория УКС дает второе пространственное решение (2.2), исходя из постулирования постоянства скорости света в упругой квантованной среде в виде комплексной скорости системы «тело- среда». При этом установлено, что увеличение скорости движе- ния системы «тело-среда» дает сжатие пространства (2.27), обес- печивая его сферическую симметрию независимо от скорости. СТО и ОТО не могли дать такого решения в принципе, посколь- ку неясно, как сжимать пустое пространство. Сжатие упругого пространства связано с совершением дополнительной работы и накоплением упругой энергии сжатой вокруг тела среды. Интен- сивность сжатия, а соответственно и упругая энергия, существенно увеличиваются на релятивистских скоростях. СТО связывает ре- лятивистское увеличение энергии с увеличение массы тела, тем самым преднамеренно нарушая закон сохранения вещества. Пос- кольку другого объяснения данному феномену не предлагалось, то научный истеблишмент вынужден был принять данную кон- цепцию. И вот, теперь теория УКС дает довольно логичное объ- яснение, связывая увеличение релятивистской энергии с увели- чением упругой энергии сферически сжатого пространства во- круг движущегося тела.

Но поскольку сжатие пространства связано с совершением дополнительной работы, то должна возникать дополнительная сила, оказывающая сопротивление движению, так называемая сила релятивистского сопротивления F_γ. Поскольку сжатие простран- ства осуществляется при увеличении скорости с V₀ до V₁, то есть в момент переходного процесса ускорения системы «тело-среда», то сила релятивистского сопротивления будет проявляться со- вместно с силой возмущающей F. В этом случае можно написать, что сила релятивистского сопротивления F_γ пропорциональна силе возмущения F

где, К_с — коэффициент сопротивления, тогда релятивистское урав- нение движения можно записать в классическом виде

или

где, n = 1, 2, 3 — показатель степени, с учетом (3.4), запишем (3.3)

или

Из (3.6) получаем привычное релятивистское уравнение [11]

Таким образом, теория УКС не ставит различия между клас- сической и релятивистской механиками. Уравнения релятивис- тской механики (3.7) могут быть легко получены из уравнений классической механики при наличии сопротивления движению упругой квантованной среды, что доказывает их инвариантность.

Для определения силы сопротивления F_γ и коэффициента К_с (3.3) воспользуемся соотношением для сжатия пространства (2.22), считая, что сфера пространства радиусом R вокруг цен- тральной массы m при увеличении скорости тела с V₀ = 0 до V₁ уменьшается до радиуса r = s, тогда

или

Далее задачу можно решать в известном плане, разбив тра- екторию сжатия на примере перемещения точки А₀ в А, по лома- ной кривой A₀—А₁— А (рис. 2). Это искусственный прием, но он позволяет произвести расчет по частям, считая, что в точке А₁ на

расстоянии R от центра 0₁ пространство сжато, что ведет к увели- чению напряженности гравитационного поля а₁ по сравнению с напряженностью а в точке A₀ до сжатия

Тогда сразу же возникает вопрос о механизме данного фе- номена, объяснение которого имеет двойное значение. Сжатие пространства и увеличение напряженности поля можно объяс- нить увеличением массы тела с увеличением его скорости, и на- оборот, увеличение массы объясняется сжатием пространства. В данном случае мы наблюдаем проявление принципа простран- ственного дуализма, когда наблюдаемое явление можно объяс- нить с двух позиций. Но если во втором случае не нарушается закон сохранения вещества, то в первом нарушение налицо. В работе [1] дается объяснение механизма явления в виде гипотезы выталкивания квантовой плотности среды из ускоряемого тела или частицы. Внешне это также будет проявляться в виде сжатия пространства или увеличения массы тела. Но данная гипотеза интересна также тем, что она позволяет установить конечность энергии любой частицы, то есть ее предельную величину при достижении ею скорости света, что избавляет релятивистские уравнения от бесконечных значений энергий.

Конечно, рассматриваемые вопросы по своей природе очень сложны, и мы можем строить определенные модели явления, уточ- няя их или заменяя на новые, но в любом случае мы будем пос- тоянно сталкиваться с проявлением принципа пространственно- го дуализма, разрешая его противоречия. Следующий этап реше- ния — наглядный пример разрешения таких противоречий. Воз- вращаясь к рис. 2, определим напряженность поля a₂ в точке А Для сжатой сферы радиусом r = s из условия

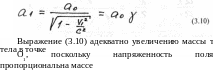
В. С.Леонов

где G=6,67 ^. 10^-11Нм²/кг² — гравитационная постоянная. Из (3.13) с учетом (3.9) получаем

)2

откуда

С учетом (3.10), из (3.15) получаем

а* - ^Qo з

Если выражение (3.10) определяет одноразовое сжатие про- странства при увеличении скорости до V,, то (3.16) описывает непрерывное сжатие пространства при увеличении V,. И в том, и в другом случае эквивалент массы определен однозначно выра- жением (3.11). В то время как (3.10) и (3.16) дают два совершенно разных релятивистских уравнения динамики, умножая их левую и правую части на массу т ускоряемого тела

Выражения (3.17) и (3.18) получены еще Эйнштейном [5] на основании преобразований Лоренца и представляют собой уравнения динамики при боковом (поперечном) действии силы (3.17) и действии ускоряющим (продольном) (3.18)

Данные уравнения хорошо изучены и проверены экспери- ментально при работе на ускорителях, и в их достоверности не приходится сомневаться. Однако их физическая природа, тракту- емая СТО, требует пересмотра. Так уравнение (3.17) связывают непосредственно с (3.11), а (3.18) — с преобразованием реляти-

24

Принимая, что

Из (3.19) находим производную по скорости

полагая, что v = dx/dt, из (3.20) с учетом (3.21) получаем

Выражение (3.21) полностью соответствует (3.18) и связано с дополнительным сжатием пространства с А₁ до А (рис. 2), а энергия (3.19) определяет упругую энергию сжатого пространст- ва. Конечно, эта версия базируется на том, что непосредственное прямое введение релятивистской массы в уравнение динамики дает только уравнение (3.17) для n = 1. Чтобы получить (3.18) для n = 3, нужно дополнительно сжать пространство, то есть кинети- ческая энергия системы «тело-среда» (3.19) связана с энергией упругой деформации пространства.

Конечно, известно, что, дифференцируя (3.11)

и преобразуя (3.20)

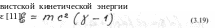
или с учетом (3.11) также получаем уравнение кинетической энер- гии (3.19)

то есть, математика позволяет свести концы с концами при вве- дении в уравнения релятивистской массы (З.П), но противоре- чия, обусловленные различием в показателях степени n=l и n=3 в релятивистских уравнениях динамики (3.17) и (3.18) с физичес- кой точки зрения объясняются сжатием упругой среды. В данном случае мы опять сталкиваемся с проявлением принципа простран- ственного дуализма, когда одинаковые результаты мы можем по- лучить, исходя из различных взглядов на одно явление, но в рам- ках инварианта Эйнштейна-Минковского. Возвращаясь к теории УКС, найдем коэффициенты сопротивления среды Кс (3.1) и (3.3) для уравнений (3.17) и (3.18), записав их в следующем виде и разлагая в ряд:

1) для n=1

откуда

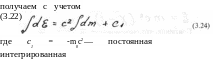
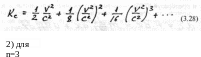
очевидно, что с точностью до третьего знака, К_с > 1. Поэтому сила сопротивления со стороны пространства всегда больше силы возмущающей, что не позволяет ускоряемой частице достичь ско- рости света.

Как видно, сопротивление движению в упругой квантован- ной среде имеют довольно сложную зависимость и проявляется только при воздействии силы F. Но есть еще одно решение для n=2, когда K_c представляет собой уравнение динамически фотон- ного излучения. Действительно, анализ (3.29) и (3.30) показыва- ет, что сила сопротивления движению пропорциональна квадра- ту скорости

где Kγ— коэффициент пропорциональности, кг/м.

Рассматривая движение фотона, значение можно опре- делить исходя из анализа свойств фотона:

1. фотон относится к частицам, которые достигают скорос- ти света;

2. это безмассовая частица, имеющая определенную энер- гию (эквивалент массы);

3. фотон имеет предельную скорость, которая обусловлена сопротивлением среды, которая, в свою очередь, уравновешива- ется силой возмущения, обусловленной энергией излучения

в этом случае, с учетом (3.21) получаем

откуда

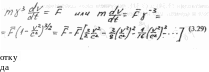
подставляя (3.34) в (3.31), получаем силу сопротивления для фо- тона в момент его излучения.

откуда

далее подставляем (3.35) в (3.2)

выражение (3.37) записываем в привычной для релятивизма форме

Итак, впервые получено уравнение (3.38) для п=2, пред- ставляющее собой динамику фотонного излучения. Это уравне- ние удалось вывести, исходя из свойств упругой квантованной среды. Поскольку данное уравнение представляет интерес для квантовой механики, то его решение мною выделено в отдель- ный раздел.