2. Определитель матрицы

Определителем (или детерминантом) квадратной матрицы размера называется число 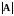, получаемое по формуле:

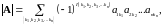
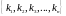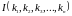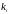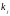где – всевозможные различные перестановки, образованные из номеров столбцов матрицы , – полное число инверсий в перестановке . Инверсией будем называть такое взаимное расположение чисел и в перестановке, при котором выполняются условия 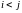и 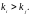Например, 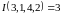. Общее число перестановок, определяющее количество слагаемых в приведенной сумме, равно .

Напомним основные свойства определителей, важных с точки зрения последующего рассмотрения некоторых численных методов:

1. При транспонировании матрицы ее определитель не меняется.

2. При перестановке двух столбцов или двух строк матрицы знак ее определителя меняется на противоположный.

3. Определитель матрицы, содержащей два линейно-зависимых столбца (или строки), равен нулю.

4. Определитель произведения матриц размера равен произведению их определителей, то есть

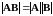
Детерминант квадратной матрицы порядка k, образованной элементами, стоящими на пересечении строк 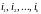и столбцов называется минором k -го порядка и обозначается .

Детерминант квадратной матрицы порядка образованной элементами, остающимися после вычеркивания строк и столбцов называется минором, дополнительным к минору , и обозначается .

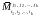Число называется алгебраическим дополнением элемента матрицы , где 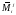– дополнительный минор элемента . Справедливы следующие равенства:

,

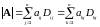Разложение определителя по i -ой строке имеет вид:

Наивысший из порядков, отличных от нуля миноров матрицы , называется рангом матрицы и обозначается 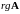. Очевидно, что если определитель матрицы не равен нулю, то её ранг равен количеству строк (столбцов), т.е. порядку матрицы.

Процедуры вычисления определителя, миноров, ранга матриц могут использоваться в анализе динамических систем, например, при проверке критерия устойчивости системы [2], условия её наблюдаемости в алгоритмах оптимальной фильтрации [3] и т.д.

1. Расчёт определителя методом Гаусса-Жордана

На практике для нахождения определителя произвольной квадратной матрицы удобно использовать метод Гаусса, состоящий в приведении матрицы к треугольному виду (такому, при котором все элементы под или над главной диагональю матрицы равны нулю). Напомним, определитель треугольной матрицы равен произведению её диагональных элементов:

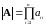, (1.1)

где – треугольная матрица, , – её диагональные элементы.

Приведение произвольной квадратной матрицы к треугольному виду состоит в следующем. Для каждой -ой строки матрицы, начиная с первой и заканчивая -ой, выполняется преобразование всех элементов, располагающихся ниже этой строки в столбцах 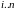, по формуле:

, , , .

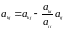Значение называют ведущим элементом на -ой итерации метода. Если на какой-то итерации значение будет равно 0, то необходимо выполнить поиск ненулевого значения в -ом столбце в строках и, при нахождении такого значения, поменять местами -ую и найденную строки. При этом необходимо вести подсчёт таких перестановок, чтобы с их учётом вычислить значение определителя (как отмечалось в предыдущем разделе, при перестановке строк или столбцов в матрице знак её определителя меняется на противоположный):

,

где – количество выполненных перестановок в процессе приведения матрицы к треугольному виду.

Если на очередном шаге при выборе ведущего элемента найти строку с ненулевым значением в -ом столбце не удалось, то это означает, что определитель матрицы равен 0.

3. LU-разложение матриц

Общепринятые обозначения L и U связаны с английскими словами «lower» (нижний) и «upper» (верхний). Существует другой вариант обозначения: L и R, определяемый словами «left» (левый) и «right» (правый).

LU-метод основан на том, что если главные миноры матрицы отличны от нуля, тогда эту матрицу можно представить, причем единственным образом, в виде произведения:

,

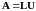где – нижняя (левая) треугольная матрица с ненулевыми диагональными элементами и – верхняя (правая) треугольная матрица с единичной диагональю:

, ,

или:

,

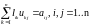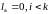
Окончательно можно записать:

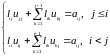
Полагая 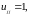получим следующие рекуррентные формулы для вычисления элементов матриц и :

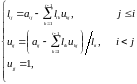
Вычисления следует начинать с левого верхнего элемента и выполнять построчно, слева направо. Вычислительная сложность данного алгоритма составляет .

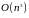С использованием найденных элементов матриц и становится возможным простое вычисление определителя исходной матрицы :