
- •Формальные средства и алгоритмы анализа и моделирования динамических систем
- •Элементарные алгебраические операции над векторами и матрицами
- •Определитель матрицы
- •Расчёт определителя методом Гаусса-Жордана
- •Разложение симметричных матриц по схеме Холецкого
- •Обратные матрицы
- •Обращение матриц методом Гаусса-Жордана
- •Обращение матриц с использованием lu-разложения
- •Обращение симметричных матриц с использованием схемы Холецкого
- •Собственные числа и векторы матриц
- •Понятие и свойства собственных чисел и векторов
- •Метод вращений Якоби решения симметричной полной проблемы собственных значений
- •Литература
Формальные средства и алгоритмы анализа и моделирования динамических систем
При описании процессов функционирования различных динамических систем (к которым относятся и бортовые интегрированные системы ЛА) в качестве базовых формальных средств, на которых основана запись математических выражений, используются векторы и матрицы.
В
математическом моделировании вектор
может рассматриваться в разных
интерпретациях. Например, в трёхмерном
евклидовом пространстве под вектором
понимают математический объект,
характеризующийся величиной и
направлением. Такой вектор всегда имеет
некоторый физический смысл (радиус-вектор,
вектор скорости, вектор силы, вектор
напряженности электрического поля и
т.д.). Если в пространстве задана система
координат, то вектор однозначно
определяется тремя числами – координатами,
например: . ..
Над множеством векторов в таком
пространстве определен ряд алгебраических
операций, таких как сложение, скалярное
и векторное умножение, вычисление
модуля, имеющих геометрический смысл
и представление. Традиционно координаты
векторов принято записывать в столбец,
поэтому при строчной записи координат
используется оператор транспонирования.
Вектор в данной интерпретации является
основным формальным средством описания
движения ЛА и процессов функционирования
связанных с его движением интегрированных
систем.
..
Над множеством векторов в таком
пространстве определен ряд алгебраических
операций, таких как сложение, скалярное
и векторное умножение, вычисление
модуля, имеющих геометрический смысл
и представление. Традиционно координаты
векторов принято записывать в столбец,
поэтому при строчной записи координат
используется оператор транспонирования.
Вектор в данной интерпретации является
основным формальным средством описания
движения ЛА и процессов функционирования
связанных с его движением интегрированных
систем.
В
наиболее общем смысле вектор может
рассматриваться как элемент некоторого
 -мерного
линейного пространства, представляющий
собой упорядоченную последовательность
из .
.
чисел – координат (вектор размерности
):
-мерного
линейного пространства, представляющий
собой упорядоченную последовательность
из .
.
чисел – координат (вектор размерности
):
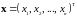 .
В таком смысле векторы используются в
обобщённой теории динамических систем.
Каждая такая система имеет некий набор
параметров различной физической природы,
характеризующих её состояние. Реально
существующая система может иметь
бесконечное или очень большое число
таких параметров, но при переходе к
математической модели этой системы
количество параметров ограничивают.
Упомянутое линейное пространство, в
котором представлено множество всех
состояний динамической системы,
определяемых возможными значениями
параметров, называется фазовым
пространством. Координаты этого
пространства называются фазовыми
переменными (переменными состояния).
Совокупность таких координат образует
вектор состояния системы. Для множества
таких векторов в общем случае отсутствует
геометрическая интерпретация, и, в
отличие от трёхкомпонентных векторов,
не определены некоторые алгебраические
операции, имеющие чисто геометрический
смысл (например, векторное произведение).
В таком смысле вектор является основным
средством формализации различных
математических моделей, алгоритмов их
исследования и анализа, процессов
функционирования динамических систем.
.
В таком смысле векторы используются в
обобщённой теории динамических систем.
Каждая такая система имеет некий набор
параметров различной физической природы,
характеризующих её состояние. Реально
существующая система может иметь
бесконечное или очень большое число
таких параметров, но при переходе к
математической модели этой системы
количество параметров ограничивают.
Упомянутое линейное пространство, в
котором представлено множество всех
состояний динамической системы,
определяемых возможными значениями
параметров, называется фазовым
пространством. Координаты этого
пространства называются фазовыми
переменными (переменными состояния).
Совокупность таких координат образует
вектор состояния системы. Для множества
таких векторов в общем случае отсутствует
геометрическая интерпретация, и, в
отличие от трёхкомпонентных векторов,
не определены некоторые алгебраические
операции, имеющие чисто геометрический
смысл (например, векторное произведение).
В таком смысле вектор является основным
средством формализации различных
математических моделей, алгоритмов их
исследования и анализа, процессов
функционирования динамических систем.
Формализация
математических моделей динамики
интегрированных систем ЛА также опирается
на понятие матрицы – упорядоченной
прямоугольной таблицы чисел, в общем
случае содержащей .. строк и
 столбцов (размерности
столбцов (размерности
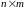 ).
Если количество строк равно количеству
столбцов, то такая матрица называется
квадратной. Так, например, квадратная
матрица размерности .
).
Если количество строк равно количеству
столбцов, то такая матрица называется
квадратной. Так, например, квадратная
матрица размерности . .
является естественной формой записи
корреляционных моментов случайных
компонент вектора состояния динамической
системы
.
является естественной формой записи
корреляционных моментов случайных
компонент вектора состояния динамической
системы
 ,
состоящего из
компонент:
,
состоящего из
компонент:
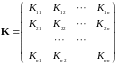 ,
,
где
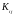 – взаимный корреляционный момент
– взаимный корреляционный момент
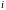 -ой
и
-ой
и
 -ой
компоненты вектора состояния, причём
-ой
компоненты вектора состояния, причём
 .
Матрица, для которой выполняется
последнее условие, называется симметричной
(симметрической).
.
Матрица, для которой выполняется
последнее условие, называется симметричной
(симметрической).
Над множеством матриц и векторов определены линейные алгебраические операции, позволяющие существенно упростить формализацию и сделать более компактной запись математических моделей интегрированных систем ЛА, состояние которых определяется в многомерном фазовом пространстве. Формальная запись расчётных соотношений, задающих, например, динамику ЛА или составляющих какие-либо алгоритмы с использованием векторов и матриц требует владения основными понятиями линейной алгебры, знания правил сложения, умножения, преобразования и свёртки векторов и матриц. Для непосредственного проведения расчётов в процессе моделирования или анализа динамических систем необходимо владение основными численными методами, реализующими перечисленные процедуры.
Далее в этом разделе будут рассмотрены понятия и правила выполнения основных алгебраических операций над множеством векторов и матриц1, а также некоторые численные методы и алгоритмы над матрицами с учётом их применения в моделировании и анализе динамики интегрированных систем ЛА.
