1.3 Правила округлений при вычислении погрешностей и результата измерений

Вопрос о точности вычисления очень важен, так как позволяет избежать большого объема лишней работы. Следует понимать, что не нужно проводить вычисления с точностью превосходящей тот предел, который обеспечивается точностью определения непосредственно измерявшихся в опыте величин. Проведя обработку измерений, часто не подсчитывают ошибки отдельных результатов и судят об ошибке приближенного значения величины, указывая количество верных значащих цифр в этом числе.

Значащими цифрами приближенного числа называются все цифры, кроме нуля, а также нуль в двух случаях:

– если нуль находится между значащими цифрами.

Пример – В числе 2053 – четыре значащих цифры;

– когда нуль стоит в конце числа и известно, что единицы соответствующего разряда в данном числе нет.

Пример – В числе 5,20 три значащих цифры. Из этого следует, что при измерении учитывались не только единицы, но и десятые, и сотые. В числе 5,2 – только две значащих цифры, поэтому, учитывались только целые и десятые.

Приближенные вычисления производятся при соблюдении следующих правил:

– при сложении и вычитании в результате сохраняют столько десятичных знаков, сколько их содержится в числе с наименьшим количеством десятичных знаков.

Пример – 0,8934+3,24+1,188=5,3214 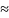5,32.

– при умножении и делении в результате сохраняют столько значащих цифр, сколько их имеет число с наименьшим количеством значащих цифр.

Пример – 8,632 2,8 3,53 = 85,318688 85,3.

Если же один из сомножителей начинается с единицы, а сомножитель, имеющий наименьшее количество цифр, – с любой другой цифры, то в результате сохраняют на одну цифру больше, чем в числе с наименьшим количеством значащих цифр.

Пример – 30,9 1,8364=56,74476 ≈ 56,74.

При вычислении промежуточных результатов сохраняют на одну цифру больше, чем прописывают приведенные выше правила (одна цифра оставляется для «запаса»). В окончательном результате цифра, оставляемая для «запаса» отбрасывается. Для уточнения значения последней значащей цифры результата, цифру, следующую за ней, следует вычислить. Если она 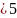, её следует просто отбросить, а если окажется 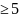, то, при её отбрасывании, предыдущую цифру нужно увеличить на единицу. Обычно в абсолютной погрешности оставляют одну значащую цифру, а измеренную величину округляют до того разряда, в котором находится значащая цифра абсолютной погрешности;

– при расчете значений функций 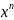, , 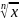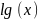некоторого приближенного числа результат должен содержать такое количество значащих цифр, сколько их имеется в числе .

Пример – .

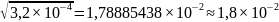Следует отметить, что абсолютную погрешность предварительно вычисляют не более, чем с двумя значащими цифрами, а в окончательном результате еще раз округляют до одной значащей цифры. Для относительной погрешности оставляют две значащие цифры.

Основное правило представления результатов состоит в том, что значение любого результата должно оканчиваться цифрой в таком десятичном разряде, что и последняя значащая цифра погрешности.

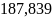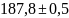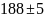Пример – Результат с погрешностью 0,5 нужно округлить до . Если этот же результат получен при погрешности 5, то его правильно представить в виде: . А если погрешность равна 50, то записываем результат, как .
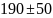