Министерство образования и науки РФ
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Институт цветных металлов и материаловедения
Кафедра фундаментального естественно-научного образования
Измерение объемов тел правильной
геометрической формы
Методические указания к лабораторной работе
Красноярск 2016
Лабораторная работа
Измерение объемов тел
правильной геометрической формы
Цель работы:
– вычислить объем твердого тела правильной геометрической формы;
– научиться обрабатывать результаты измерений и оценивать точность измеряемой величины посредством погрешностей.
Приборы и принадлежности: тело цилиндрической формы, штангенциркуль.
1 Основные положения теории погрешностей
Курс физики составляет основу базовой подготовки инженера любой специальности. Поскольку физика – наука экспериментальная, то выполнение лабораторных работ в учебных лабораториях является неотъемлемой частью физического образования студента. Получая опытные данные, в процессе проведения физического эксперимента, обучающийся должен уметь обрабатывать его результаты. Поэтому, прежде всего, необходимо освоить приемы и методы расчета погрешностей измеряемых величин, поскольку любая физическая величина, в результате влияния многих объективных и субъективных причин, может быть измерена лишь приближенно, с некоторой точностью.
В данном разделе описана методика обработки результатов измерений, в основе которой лежит наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности – метроло́гия. Метрология, опираясь на результаты математической статистики, предоставляет сведения относительно того, как следует обрабатывать результаты измерений количественной информации о свойствах объектов окружающего нас мира с заданной точностью и достоверностью.
1.1 Прямые и косвенные измерения. Виды погрешностей
Целью любого физического эксперимента является измерение физических величин, которые характеризуют изучаемое явление. Результатом отдельного измерения, часто называемого наблюдением, служит численное значение измеряемой величины.
Измерение величины: процесс экспериментального получения одного или более значений величины, которые могут быть обоснованно приписаны величине. Измерение подразумевает сравнение величин или включает счет объектов. Измеряемая величина может быть соотнесена с другой эталонной величиной, принятой за единицу измерения.
Пример – Измерения меры длины, выполненные путем сравнения с эталонной мерой на штангенциркуле.
Результат измерения физической величины; результат измерения; результат: значение величины, полученное путем её измерения.
По способу получения результата измерения физической величины, выделяют прямые, косвенные и совместные измерения.
Прямое измерение: измерение, при котором искомое значение величины получают непосредственно от средства измерений.
Примеры
Измерение длины детали микрометром.
Измерение силы тока амперметром.
Измерение массы тела на весах.
Зачастую, прямое измерение оказывается невозможным или очень трудоемким, требующим специфического физического оборудования. Но физическая величина, значение которой нужно определить, может быть связана по известной из теории формуле с другими величинами. Последние измеряются в результате прямых измерений и их результаты, затем подставляются в формульное выражение. Такой метод измерения и называется косвенным.
Косвенное измерение: измерение, при котором искомое значение величины определяется на основании результатов прямых измерений других величин, функционально связанных с искомой величиной.
Пример
– Определение плотности
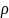тела, имеющего правильную цилиндрическую
форму, по результатам прямых измерений
массы
,
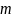высоты
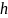и диаметра цилиндра
,
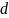по формуле
|
|
.
Совместные измерения: проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними. Совместные измерения позволяют получать пары чисел, необходимые для построения графиков. Так, например, при каждом значении сопротивления электрической цепи получают пары значений напряжения и силы тока.
Опыт показывает, что любая физическая величина измеряется с некоторой погрешностью (ошибкой), что является неотъемлемой составляющей любого эксперимента. Поэтому измерение должно оканчиваться расчетом точности и достоверности полученного значения измеряемой величины.
Погрешность измерения: разность между результатом измерения и истинным значением величины.
В
курсе математической статистики
доказывается, что наилучшей
оценкой истинного значения
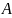измеряемой величины
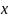является ее среднее арифметическое
значение
.
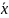Его определение
дано в подразделе 1.4.
Для вычисления среднего арифметического значения необходимо выполнить многократные измерения физической величины.
Под многократными измерениями понимают не менее четырех измерений.
Погрешности измерения, по характеру происхождения и по способам исключения их влияния на значение измеряемой величины, делятся на три вида: случайные; систематические; грубые погрешности (промахи).
Случайная погрешность, которая является составляющей погрешности измерения, это погрешность, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью. Случайная погрешность обусловлена действием различных помех на измерительные приборы. Её нельзя исключить вообще, но можно уменьшить ее влияние на значение измеряемой величины путем многократного повторения эксперимента. Случайные факторы, действующие на объект измерения и измерительные приборы, всегда присутствуют в эксперименте и возникают вследствие самых различных причин изменения температуры, давления, влажности воздуха, наличия электрических и магнитных полей, вибрации и т.д.
Неисключенная систематическая погрешность (НСП) или систематическая погрешность: составляющая погрешности измерения, которая включает погрешность метода измерений, средства измерений и другие источники погрешности. Систематическая погрешность остается постоянной или же закономерно изменяется при повторных измерениях одной и той же величины. Систематическая погрешность определяется ограниченной точностью прибора и метода измерений, когда экспериментатор вынужден округлять значение величины при её считывании со шкалы прибора. Такая погрешность может быть вызвана, например, изогнутостью стрелки прибора, смещением «нуля» прибора и т.п. Следует отметить, что систематические погрешности не уменьшаются при возрастании числа измерений. Оценкой систематической погрешности служат доверительные границы систематической погрешности измерительного прибора.
Грубая погрешность: погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей. Грубые погрешности являются результатом неправильного отсчета по прибору, нарушением условий измерений, неисправности прибора, недосмотра экспериментатора или неправильно выбранной методики измерений. Главным признаком грубой погрешности является резкое отличие значения физической величины от ее значений, полученных в других измерениях. Результаты измерения, в котором обнаружена грубая погрешность, аннулируются.
Погрешность измерения складывается из случайной и систематической погрешностей.
Таким образом, после проведения измерений в расчетах учитываются только систематические и случайные погрешности.
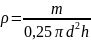