Произведем корректировку данной системы автоматического регулирования.
2.1. По номограммам качества Солодовникова
для определения частоты среза системы
по перерегулированию
и времени регулирования
найдем
желаемую частоту среза.
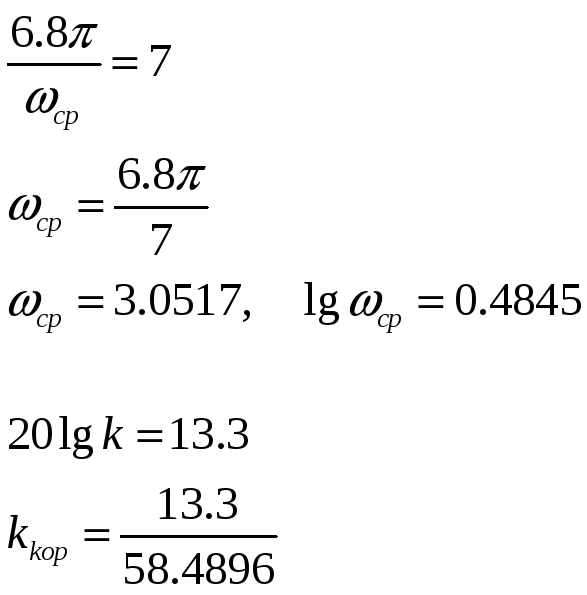
Введем полученный коэффициент коррекции в систему и проверим алгебраическими и частотными критериями устойчивости насколько правильно подобрано корректирующее звено.
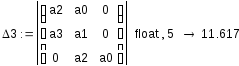
2.2. Алгебраический критерий устойчивости. Критерий определителей Гурвица.
Исходные значения коэффициентов передачи
Передаточная функция разомкнутой системы управления
Передаточная функция замкнутой системы управления
Передаточные функции элементов системы:
2.3. Частотный критерий устойчивости Михайлова.
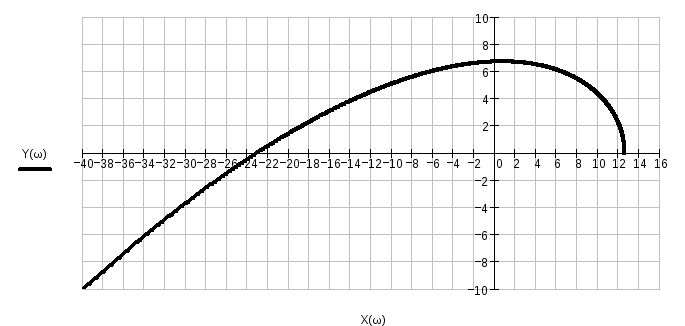
Система устойчива, т.к. годограф
Михайлова САУ, представленной передаточной
функцией
начинается при частоте
на вещественной положительной полуоси,
не нарушает последовательности обхода
квадрантов координатной плоскости
против часовой стрелки, нигде не обращаясь
в ноль и не пересекается сам с собой.
2.4. Частотный критерий устойчивости Найквиста.
По частному случаю частотного критерия
Гурвица для системы
третьего порядка:
,
,
делаем вывод, что разомкнутая система
устойчива.
Из комплексного коэффициента передачи
выделим мнимую и вещественную частотные характеристики
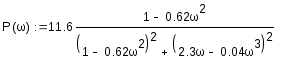
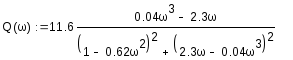
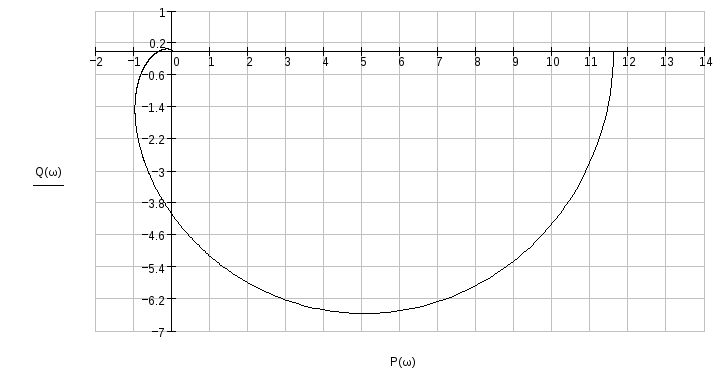
Замкнутая система является устойчивой,
т.к. годограф Найквиста для разомкнутой
системы, представленной передаточной
функцией
являющейся устойчивой, не охватывает
точку (-1;j0).
2.5. Логарифмические частотные характеристики. Проверка запасов устойчивости системы.
Передаточная функция разомкнутой
системы
1
)
- апериодическое звено
с наклоном
2
)
3 )
- апериодическое звено с наклоном
4 )
- апериодическое звено с наклоном
ЛАЧХ нескорректированной системы:
ФЧХ скорректированной системы:
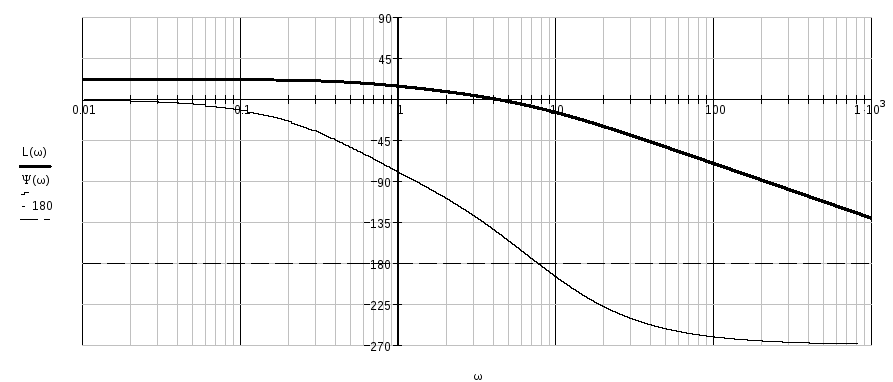
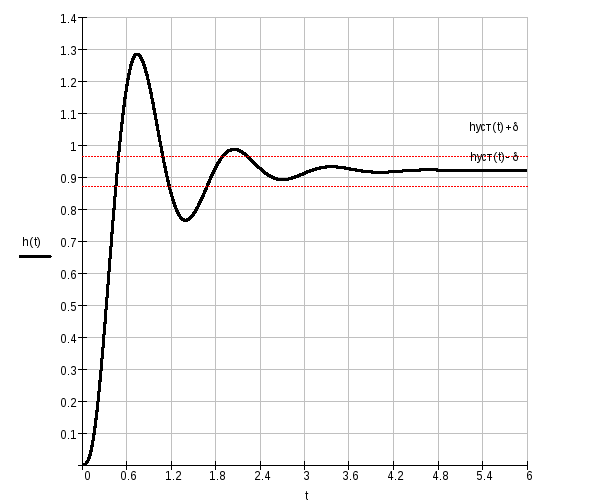
2.6. Построим переходную характеристику скорректированной системы автоматического регулирования при помощи обратного преобразования Лапласа.
=
+
+
+
+
2.7. Построим весовую функцию скорректированной системы автоматического регулирования.
=
+
+
+
+
2.8. Построим график ошибки скорректированной системы автоматического регулирования.
=
+
+
+
+
-
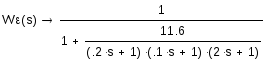
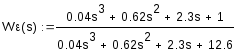
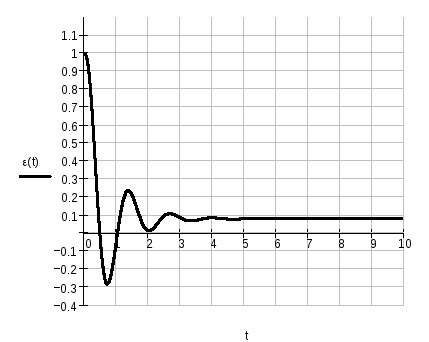
Рассмотрим примеры систем автоматического регулирования, которые могут функционировать с учетом приведенный параметров. Существует несколько видов систем регулирования уровня жидкости в емкости. Рассмотрим некоторые из них:
-
Поплавковый регулятор
Простым примеров этой системы может быть сливной бачок унитаза.
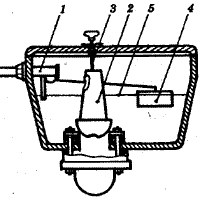
1 - поплавковый клапан; 2 - груша, совмещенная с переливом; 3 - тяга; 4 - поплавок; 5 - уровень воды.
-
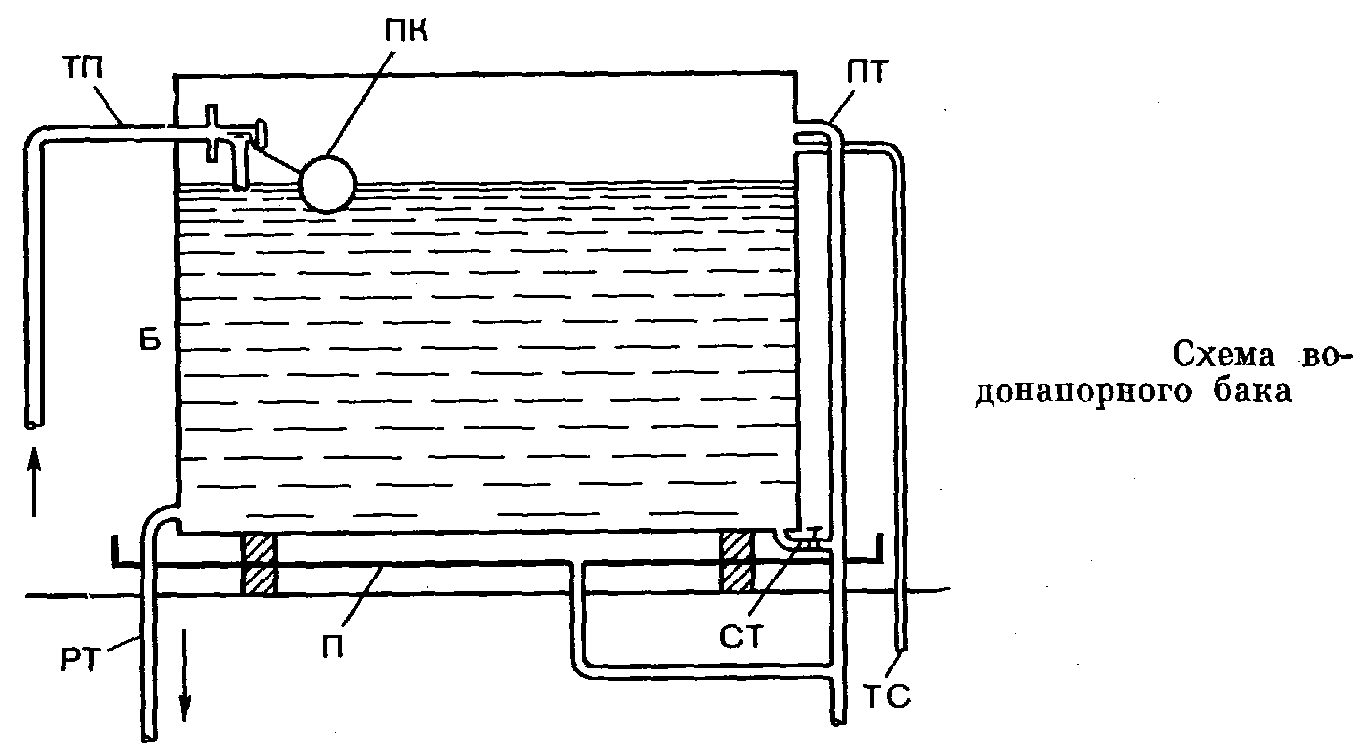
Двухпозиционный регулятор
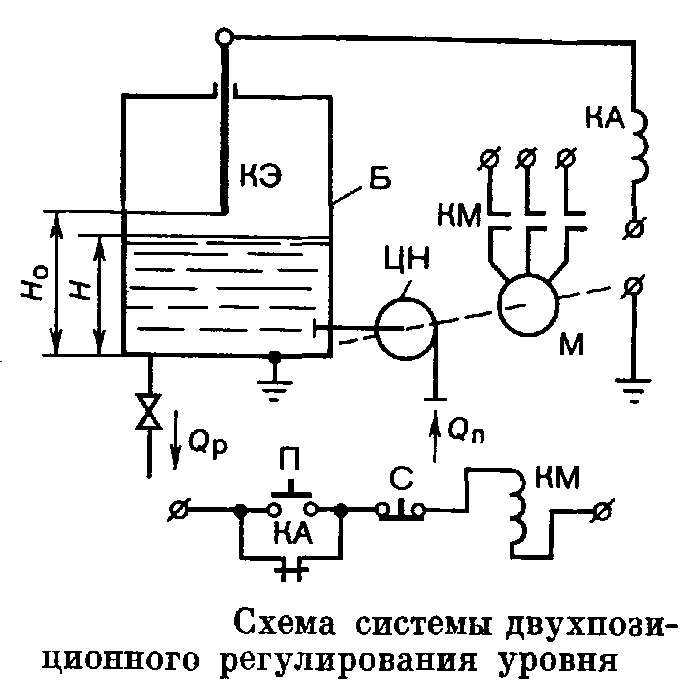
Примером этого типа регулятора может служить система автоматического управления уровнем жидкости
назначение Система совместно с исполнительными механизмами (насосами и др.) предназначена для:
-
автоматического регулирования уровня жидкости в открытых емкостях, отстойниках, накопителях
-
выдачи непрерывного сигнала (0....5)mA по уровню в другие системы
-
визуального контроля за уровнем жидкости.