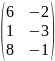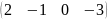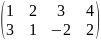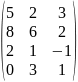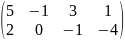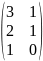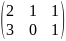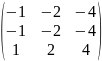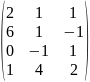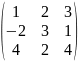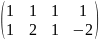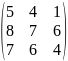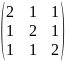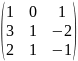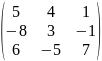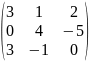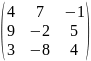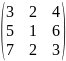- •Санкт-Петербургский колледж телекоммуникаций
- •Раздел 1. Элементы линейной алгебры тема «матрицы и определители»
- •Содержание
- •Введение
- •Указания по выполнению контрольных работ
- •III. Краткие сведения из теории
- •1) Понятие матрицы
- •2) Действия над матрицами
- •3) Понятие определителя
- •4) Основные свойства определителей
- •Вычислить определители:
- •Вычислить определители:
- •Напомним: а) что определитель выгоднее раскрывать по той строке (столбцу), где:
- •Б) свойства определителей, которые полезно знать:
- •2. Выполнить действия над матрицами:
- •5. Решить матричное уравнение:
- •VI. Вопросы для самоконтроля по теме:
2. Выполнить действия над матрицами:
Даны матрицы А и В. Найти матрицу С.
N варианта |
Матрица А |
Матрица В |
Матрица С |
|
|
|
|
С=2АТ |
|
|
|
|
С=ЕА |
|
|
|
|
С=АТ |
|
|
|
|
С=2АТ ВТ |
|
|
|
|
С=АТ |
|
|
|
|
С=3В АТ |
|
|
|
|
С=А В)Т |
|
|
|
|
С=АТ |
|
|
|
|
С=2А В |
|
|
|
|
С=2А В |
|
|
|
|
С=3А ВТ |
|
|
|
|
С=3А В |
|
|
|
|
С=2В АТ |
|
|
|
|
С=А ВТ |
|
|
|
|
С=3В |
|
|
|
|
С=(2В)Т А |
|
|
|
|
С=2А ВТ |
|
|
|
|
С=АТ ВТ |
|
|
|
|
С=2А |
|
|
|
|
С=(3А)Т В |
|
|
|
|
С=В 2АТ |
|
|
|
|
С=2ВТ (2А)Т |
|
|
|
|
С=(2А)Т В |
|
|
|
|
С=3В 2АТ |
|
|
|
|
С=А 3В |
ОБРАЗЕЦ ВЫПОЛНЕНИЯ 0-го варианта 2-го задания:
2. Действия над матрицами. Даны матрицы А и В. Найти матрицу С.
N варианта |
Матрица А |
Матрица В |
Матрица С |
2.0 |
|
|
С=2АТ ВТ |
С=2АТ ВТ
Для вычисления данного выражения необходимо транспонировать заданные матрицы, т.е. поменять строки и столбцы местами:
 ,
т.е.
,
т.е.
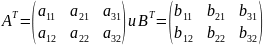 , затем умножить соответствующую матрицу
на коэффициент, заданный в выражении,
и произвести вычисления:
, затем умножить соответствующую матрицу
на коэффициент, заданный в выражении,
и произвести вычисления:

 .
.
Ответ:

3.ВЫЧИСЛИТЬ ПРОИЗВЕДЕНИЕ МАТРИЦ А∙В. Проверить, существует ли произведение В∙А, если существует – вычислить.
N варианта |
Матрица А |
Матрица В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОБРАЗЕЦ ВЫПОЛНЕНИЯ 0-го варианта 3-го задания:
3. Вычислить произведение матриц А∙В. Проверить, существует ли произведение В∙А.
N варианта |
Матрица А |
Матрица В |
3.0 |
|
|
Условием существования произведения матриц является их согласованность», т.е. количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. Матрица А имеет 1 строку и 4 столбца. матрица В – 4 строки и 2 столбца. Следовательно, произведение А∙В возможно, а В∙А посчитать невозможно:
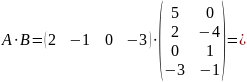


Ответ:
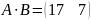
4. НАЙТИ ОБРАТНУЮ МАТРИЦУ ДЛЯ МАТРИЦЫ А. Сделать проверку.
N варианта |
Матрица А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОБРАЗЕЦ ВЫПОЛНЕНИЯ 0-го варианта 4-го задания:
4. Найти обратную матрицу для матрицы А. Сделать проверку.
N варианта |
Матрица А |
4.0 |
|
Найдите
обратную матрицу для матрицы
 .
.
Решение. Находим определитель

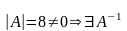 ,
т.е. матрица
,
т.е. матрица
![]() -
невырожденная, и обратная для нее
существует.
-
невырожденная, и обратная для нее
существует.
Находим алгебраические дополнения:




 Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй – строке. Полученная матрица
и служит ответом.
Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй – строке. Полученная матрица
и служит ответом.

Для
проверки правильности нахождения
обратной матрицы, необходимо произвести
умножение матрицы А на матрицу
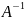 .
Их произведение должно быть равно
матрице
.
Их произведение должно быть равно
матрице
 .
В противном случае – обратная матрица
найдена ошибочно, необходимо переделать
задание.
.
В противном случае – обратная матрица
найдена ошибочно, необходимо переделать
задание.
 .
.



 ВТ
ВТ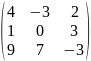

 ВТ
ВТ

 ВТ
ВТ



 ВТ
ВТ




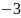 В
В


















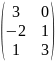

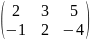

 В
В