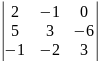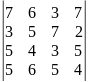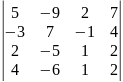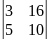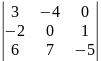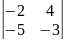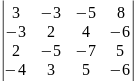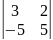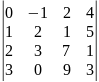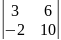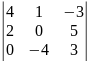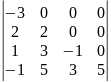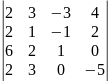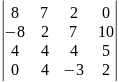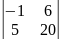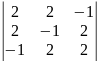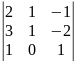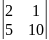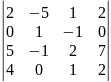1. Вычислить определители:

N варианта	Определитель 2-го порядка	Определитель 3-го порядка	Определитель 4-го порядка

ОБРАЗЕЦ ВЫПОЛНЕНИЯ 0-го варианта 1-го задания:

1. Вычислить определители:

N варианта	Определитель 2-го порядка	Определитель 3-го порядка	Определитель 4-го порядка
0.1

1. Определителем 2-го порядка называется число , которое определяется равенством: . .

2. Определителем 3-го порядка называется число , которое определяется, в частности, равенством:

,

(разложение определителя третьего порядка по элементам первой строки). Аналогично определитель 3-го порядка можно разложить по элементам других строк или столбцов.

3. Определителем 4-го порядка называется число , которое определяется, в частности, равенством:

(разложение определителя четвертого порядка по элементам первой строки). Аналогично определитель 4-го порядка можно разложить по элементам других строк или столбцов.

Ответ: 15, -20, -80.

Напомним: а) что определитель выгоднее раскрывать по той строке (столбцу), где:

1) нулей побольше; 2) числа поменьше;

3) .

Б) свойства определителей, которые полезно знать:

1) Величина определителя не меняется при транспонировании.

2) Любая парная перестановка строк (столбцов) меняет знак определителя на противоположный.

3) Из строки (столбца) определителя можно вынести множитель (и внести его обратно).

4) Если строки (столбцы) определителя пропорциональны, то он равен нулю. Определитель с нулевой строкой (столбцом) равен нулю.