Практичне заняття

Розв’язування задач на згасаючі та вимушені коливання

Мета: допомогти студентам застосовувати теоретичні знання з основ теорії коливальних процесів при розв’язуванні задач

Основні теоретичні положення

1.Вільні згасаючі коливання

МЕХАНІЧНІ КОЛИВАННЯ

Р івняння руху

У реальних коливальних системах повна енергія з плином часу змен­шуеться через те, що система витрачае свою енергію на роботу проти зовнішніх неконсервативних сил, таких як сили тертя, або сили опору. Енергія коливань пропорційна до квадрата амшптуди iіз зменшенням енергії амплітуда коливань також зменшуеться, коливання «загасають».

У найпростішому випадку сила опору пропорційна до швидкості:

де r –коефіцієнт опору

На рис. 1 схематично зображено коливальну систему, яка здійснюватиме вільні згасаючі коливання. Окрім інерційної маси m і пружного елемента, жорсткість якого k, додано ще “ елемент опору ” у вигляді пластинки,зануреної у в`язку рідину. Згідно з основним законом динаміки

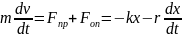
Поділивши на m і ввівши позначення

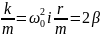
Дістанемо ДИФЕРЕНЦІАЛЬНЕ РІВНЯННЯ ВІЛЬНИХ ЗГАСАЮЧИХ МЕХАНІЧНИХ КОЛИВАНЬ

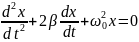
г рафік цієї функції наведено на рис. 2. Амплітуда коливань зменшується з часом за експоненціальним законом

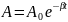
Він характеризує відношення сил опору і сил інерції.

Величину, обернену до коефіцієнта загасання, називають ЧАСОМ РЕЛАКСАЦІЇ. Це час, за який амплітуда коливань зменшуеться в е разів.

Тоді амплітуда: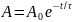

Ч астота загасаючих коливань

Вона тим менша, чим більший коефіцієнт загасання коливань тобто чим більшу роль відіграють сили опору тим .

П еріод загасаючих коливань: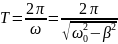

Якщо сили опору настільки великі, що β=ω₀ , то T∞. Це означає, що періодичний процес перетворюється на АПЕРІОДИЧНИЙ. Графік аперіодичного процесу наведенона Рис. 3 .У цьому разі виведена зі стану рівноваги система, що має початкову потенціальну енергію, повністю витрачає її на роботу проти сил опору упродовж одного періоду.

Характеристики загасання коливань

КОЕФІЦІЄНТ ЗАГАСАННЯ КОЛИВАНЬ

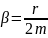
ЧАС РЕЛАКСАЦІЇ 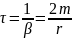— час, за який амплітуда коливань зменшується в е раз.

ДЕКРЕМЕНТ ЗАГАСАННЯ КОЛИВАНЬ дорівнює відношенню двох сусідніх, амплітуд:

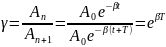
ЛОГАРИФМІЧНИЙ ДЕКРЕМЕНТ ЗАГАСАННЯ КОЛИВАНЬ

ДОБРОТНІСТЬ — це енергетична характеристика загасання коливань. Вона характеризує швидкість втрати енергії і визначається за формулою

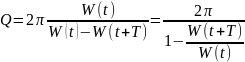
де W(t)— енергія системи в момент часу t;

W (t + Т) — енергія системи через одне повне коливання.

Оскільки енергія пропорційна до квадрата амплітуди, то виконується рівність:

При малих значеннях логарифмічного декремента загасання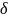 функцію ²⁸ можна розкласти в ряд і обмежитись першими двома його членами:

Тоді

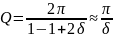
О тже, добротність обернено пропорційна до логарифмічного декремента загасання коливань. Можна дістати й інші формули для розрахунків добротності, якщо скористатися здобутими раніше співвідношеннями:

Ось ці формули:

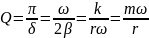
На рис. 4 наведено графіки коливань для систем з різною добротні­стю ( 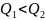). Чим більша добротність, тим повільніше загасають коли­вання. Обчислювати добротність за наведеними щойно формулами до­волі важко.

Можна це зробити простіше, знаючи кількість N коливань, після здійснення яких амплітуда зменшиться в е раз.

Справді, якщо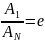 , то логарифмічний декремент загасання ко­ливань буде