
Методичні вказівки до розв’язання задач
Типові задачі по даній темі,які розв’язуються в загальному курсі фізики, можуть мати межі:
1.Розрахунок основних характеристик (напруженості та потенціалу) електростатичного поля.
2.Обчислення сил взаємодії тіл.
3. Визначення заряду, розподіленого по поверхні ізольованого провідника, розміри і форму якого задано.
1.
Щоб правильно обрати методику розв'язання
задач першої групи, доцільно встановити,
чим утворюється поле: а) системою довільно
розміщених точкових зарядів ( )
зарядами, неперервно розподіленими у
просторі на тілах правильної геометричної
форми.
)
зарядами, неперервно розподіленими у
просторі на тілах правильної геометричної
форми.
Якщо поле створюється системою довільно розташованих зарядів напруженість і потенціал результуючого поля визначаються згідно з принципом суперпозиції полів. Цей принцип можна застосувати також тоді, коли заряди неперервно розподілені у просторі, тобто для зарядженого тіла. Для цього заряд, зосереджений на поверхні, розбивають на такі елементарні заряди, щоб до кожного з них була застосовна формула напруженості або потенціалу поля точкового заряду.
Якщо поле створюється зарядами, розподіленими у просторі, то для визначення напруженості доцільно використовувати теорему Гаусса. Якщо вира?, напруженості відомий, то інтегруванням його у відповідних межах можна знайти також ьлраз для потенціалу . Для цього користуються формулою звязку.чїж напруженістю та потенціалом, тобто

2. Сили взаємодії точкових зарядів визначають за законом Кулона. Якщо таких зарядів багато, то результуюча сила знаходиться згідно з принципом суперпозиції полів.
У інших випадках силу взаємодії між зарядженими тілами ( наприклад, сила взаємодії між пластинами конденсатора) доцільніше визначати відповідно рівнянню

3. Задачі на визначення заряду розподіленого на поверхні ізольованого провідника, розміри і форму якого задано, зводяться до того, щоб знайти такий розподіл густини а на поверхні провідника, при якому в усіх його внутрішніх точках потенціал однаковий.
Приклади розв’язання задач
Задача 1.
Відстань
між двома точковими зарядами
 та
та
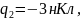 які розташовані у вакуумі, дорівнює
які розташовані у вакуумі, дорівнює
 У точці, що знаходиться на відстані
У точці, що знаходиться на відстані
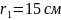 від першого та на відстані
від першого та на відстані
 від другого заряду, визначити: 1)
напруженість
;
2) потенціал
.
від другого заряду, визначити: 1)
напруженість
;
2) потенціал
.
Д ано: Розв’язання

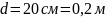
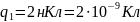
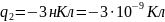

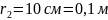

Знайдемо напруженість поля у точці А.
Згідно з принципом суперпозиції.
де – сумарна напруженість поля у точці А.
 – напруженість
полів, які створюються зарядами
– напруженість
полів, які створюються зарядами
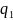 та
та
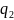 .
.
Для
визначення
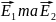 скористаємося
формулами:
скористаємося
формулами:
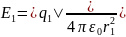 ,
,

Модуль вектора знайдемо за теоремою косинусів
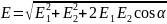
Де 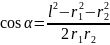
Тоді
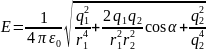
Після обчислення за цією формулою одержимо Е=3 кВ/м.
Знайдемо потенціал поля у точці А. Згідно з принципом суперпозиції, потенціал результуючого поля

Для
визначення
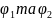 скористаємось формулами
скористаємось формулами
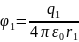 ,
,
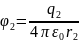
Тоді

Після
обчислення за цією формулою одержимо

Задача 2.
Електростатичне
поле створюється нескінченно довгим
циліндром радіусом
 ,
рівномірно зарядженим з лінійною
густиною
,
рівномірно зарядженим з лінійною
густиною
 Визначити 1)напруженість поля Е у точках,
які знаходяться від осі циліндра на
відстанях
Визначити 1)напруженість поля Е у точках,
які знаходяться від осі циліндра на
відстанях
 та
та
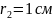 ;
2) різницю потенціалів між двома точками
цього поля, які знаходяться на відстані
;
2) різницю потенціалів між двома точками
цього поля, які знаходяться на відстані
 та
та
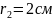 від поверхні циліндра у середній його
частині.
від поверхні циліндра у середній його
частині.
Д ано: Розв’язання


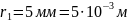
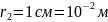
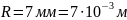

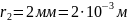

Визначимо напруженість поля.
Згідно з теоремою Гаусса
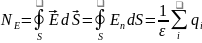
(будемо
вважати, що циркуляція вектора Е
відбувається вздовж замкненої поверхні
циліндра радіусом
 та
висотою
та
висотою
 ).
).
Якщо
 ,то
всередині замкненої поверхні зарядів
немає, тому в цій області Е=0. Потік
,то
всередині замкненої поверхні зарядів
немає, тому в цій області Е=0. Потік
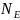 через основи коаксіального циліндра
дорівнює нулю, тому що лінії напруженості
паралельні основам циліндра. Потік
через бічну поверхню дорівнює
через основи коаксіального циліндра
дорівнює нулю, тому що лінії напруженості
паралельні основам циліндра. Потік
через бічну поверхню дорівнює
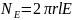 .
.
Якщо
 ,
то потік
через бічну поверхню дорівнює
,
то потік
через бічну поверхню дорівнює
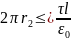
Тоді

Після
обчислення за цією формулою одержимо
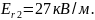
Визначимо потенціал поля.
Будемо виходити з того,що

а з осьовою симетрією

Підставимо
у (2) вираз для напруженості поля, яке
створюється нескінченно довгим циліндром
 .
.
Тоді  .
.
Для визначення різниці потенціалів проінтегруємо вираз(3)
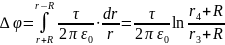
Після обчислення одержимо ∆φ=125В.
Задача 3.
Електричне поле створюється двома зарядами 4мкКл та -2мкКл, що знаходиться на відстані 0,1м один від одного. Визначте роботу сил поля з переміщенню заряду 50нКл з точки 1 у точку 2.
Дано: Розв’язання
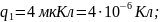 Робота
здійснювана
в електростатичному
Робота
здійснювана
в електростатичному
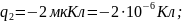 полі,
полі,
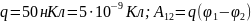
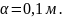 де
де
 – потенціали
поля в точках 1 і 2.
– потенціали
поля в точках 1 і 2.

Застосовуючи принцип суперпозиції полів, визначаємо потенціали:
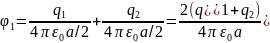


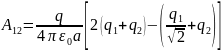
Або

Виконуємо обчислення:

Відповідь:
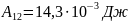 .
.
Задача 4.
Визначте
різницю потенціалів, яку повинен пройти
в електричному полі електрон зі швидкістю
 м/с для того, щоб його швидкість зросла
удвоє.
м/с для того, щоб його швидкість зросла
удвоє.
Д ано: Розв’язання
 Прискорювальну
різницю потенціалів можна знайти,
Прискорювальну
різницю потенціалів можна знайти,
 обчисливши
роботу сил електростатичного поля, що
обчисливши
роботу сил електростатичного поля, що
визначається добутком заряду електрона на різницю
 потенціалів:
потенціалів:
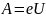
Робота сил електростатичного поля в даному випадку дорівнює зміні кінетичної енергії електрона:

де
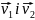 - швидкості електрона до та після
проходження прискорювального поля
відповідно.
- швидкості електрона до та після
проходження прискорювального поля
відповідно.
Прирівнявши праві частини виразів, одержуємо

Де
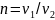 .
.
Звідси шукана різниця потенціалів:
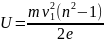
Виконуємо обчислення:
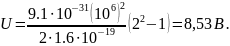
Задача 10. Дві однакові кульки масою 0.2 г кожна підвішені на нитках завдовжки 50 см. Після надання кулькам однакових зарядів, вони відхилилися на відстань 10 см. Визначити заряди, які були передані кулькам.
Д
ано:
Розв’язання
 = m
= 0,2 г
На
кожну кульку (мал. 162) діють сила
= m
= 0,2 г
На
кожну кульку (мал. 162) діють сила
 кг
тяжіння
кг
тяжіння
 =m
=m ,
силя натягу нитки
і
,
силя натягу нитки
і
l = 50 см = 0,5 м
електрична
сила взаємодії кульок
.
r
= 10 см = 0,1 м.
= 50 см = 0,5 м
електрична
сила взаємодії кульок
.
r
= 10 см = 0,1 м.
q=?
Запишемо умову рівноваги для кожної кульки у векторній формі:
 +
+
+
+
 = 0
= 0
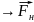 +
+ m
= 0
+
+ m
= 0
Виберемо
осі координат, як показано на малюнку,
і запишемо рівняння рівноваги враховуючи
, що

- у проекції на вісь Х:

-у
проекції на вісь Y;
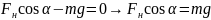 .
.
Розділяємо почленно перше рівняння на друге:
 =
=
 =
=
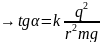
Оскільки
кут
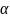 малий, то tg
малий, то tg .
Тоді:
.
Тоді:
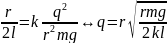
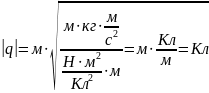
Обчислення:
q=0,1 Відповідь:
Заряд кожної кульки q
=
Відповідь:
Заряд кожної кульки q
=
 (Кл).
(Кл).
Задача 11.
П лоский конденсатор, площа пластини якого S, а відстань між якими d. Має ізолятор зі скляної пластини. Конденсатор зарядили до напруги U, після чого від’єднали.
Дано: Розв’язання
 На
нижню
кульку діє сила тяжіння
,
На
нижню
кульку діє сила тяжіння
,
 силя
тягу нитки
силя
тягу нитки
 і
електрична сила
і
електрична сила
 взаємодії
зарядів
взаємодії
зарядів

На верхню кульку діє сила тяжіння
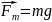 ,
сили натягу
,
сили натягу
 ниток і електрична сила взаємодії
зарядів
ниток і електрична сила взаємодії
зарядів
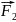 .
.
Умова
рівноваги для нижньої кульки:

Умова
рівноваги для верхньої кульки:
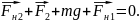
Виберемо напрям осі У, як показано на малюнку, і запишемо умову рівноваги для нижньої і верхньої кульок:
Для
нижньої:

Для
верхньої:

Враховуючи,
що
 ,
знаходимо
силу взаємодії електричних зарядів:
,
знаходимо
силу взаємодії електричних зарядів:
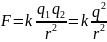
Тобто:
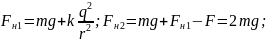

Обчислення:

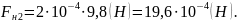
Відповідь:

Задача 12. Металева сфера, радіус якої 10 см, заряжена до потенціалу 200 В. Знайти потенціал і напруженість поля у точці, віддаленій від поверхні сфери на 5 см.
Д ано: Розв’язання
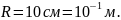 Потенціал
поля, створеного зарядженою сферою в
Потенціал
поля, створеного зарядженою сферою в
 точці
А, визначимо за формулою:
точці
А, визначимо за формулою:
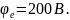
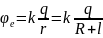
Напруженість поля в точці А:


Заряд
сфери знайдемо із формули:

Тоді

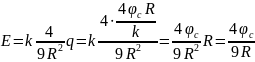 ;
;
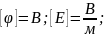
Обчислення

Відповідь:

Задача
13. Рівномірно заряджена куля радіусом
2 см у вакуумі має поверхневу густину
заряду
 Кл/
Кл/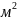 .
Визначити потенціал поля в точці
віддаленій на 0,5 см від центра куоі, а
також потенціал напруженість поля
всередині кулі.
.
Визначити потенціал поля в точці
віддаленій на 0,5 см від центра куоі, а
також потенціал напруженість поля
всередині кулі.
Дано:
R
= 2 см; δ = 5 Кл/
;
r
= 0,5м.
Знайти:
Кл/
;
r
= 0,5м.
Знайти:
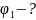 ;
E
- ?;
;
E
- ?;
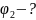
Розв’язання. Потенціал поза кулею:
= Так
як q
= δS
= δ
Так
як q
= δS
= δ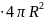 ,
то
,
то
 = 50 В
Потенціал поля всередині
зарядженої кулі:
= 50 В
Потенціал поля всередині
зарядженої кулі:
 =
=
 =
=
 В
зв'язок напруженості поля з
потенціалом
В
зв'язок напруженості поля з
потенціалом
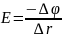 ;
Потенціал поля всередині кулі у всіх
точках однаковий, отже E
= 0. Відповідь:
;
Потенціал поля всередині кулі у всіх
точках однаковий, отже E
= 0. Відповідь:
 ;
;
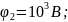 E
= 0;
E
= 0;
Задача
14. Різниця потенціалів точок, віддалених
від зарядженої площини на відстані 5 і
10 см дорівнює 5 В. Чому дорівнює заряд
площини у вакуумі, якщо її площа
400 ?
Дано:
?
Дано:
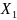 =
=
 ;
;
 ;
S
= 4
;
S
= 4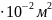 ;
;
 ;
ε = 1.
Знайти: q
- ?
Розв’язання. Різниця потенціалів
точок поля зарядженої площини
;
ε = 1.
Знайти: q
- ?
Розв’язання. Різниця потенціалів
точок поля зарядженої площини
 (
(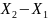 ),
де поверхнева густина
),
де поверхнева густина
 Заряд
площини: q
=
Заряд
площини: q
=
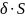 або
або
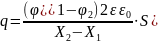 =
=
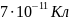 Відповідь:
q
=
.
Відповідь:
q
=
.
