Приклади розв’язування задач

Задача 1

По відрізку прямого провідника довжиною 10 см протікає струм 2 А. Визначити напруженість магнітного поля цього струму в точці, що лежить на перпендикулярі до середини відрізка і віддалена від нього на 6 см.

Дано: Розв’язання

l =10см=0,1м; Для визначення напруженості магнітного поля

скористаємося законом Біо-Савара-Лапласа.

I=2А; (1)

де — кут між напрямком струму і радіус-вектором r

який проведено від елемента струму 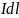в точку, в

Знайти: Н-? якій визначається напруженість поля.

Щ об обчислити інтеграл (1), пе­ретворимо підінтегральний вираз. Із рисунка випливає, що Підставляючи вирази dl і r у формулу (1), одержуємо . Оскільки Перевіримо одиниці найменування Н у формулі (2): Значення кута знайдемо зі співвідношення . Підставивши числові значення в формулу(3), одержимо . Отже,

Відповідь:

Задача 2

Два паралельних нескінченно довгих провідника, по яких течуть в одному напрямку струми І=60 А, розташовані на відстані d=10 см один від одного. Визначити індукцію магнітного поля в точці, яка міститься на відстані =5 см від одного і =12 см від іншого провідника.

Д ано: Розв’язання

І=60 А Для знаходження індукції магнітного поля В в заданій точці d=10 см=0,1м А(рисунок) визначимо напрямки індукції і полів кож­ =5 см=0,05м ного із струмів у точці А і додамо їх геометрично

=12 см=0,12м

Знайти: В-? Абсолютне значення індукції В можна знайти,

застосувавши теорему косинусів.

, де α – кут між векторами ;

Індукції магнітного поля виражаються відповідно через силу струму І та відстані . , . Підставляючи у формулу (1) В₁ і В₂, маємо

. Перевіримо найменування шуканої величини:

.

Обчислимо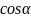 . З рисунка видно, що =куту DAC (як кути із взаєм­но перпендикулярними сторонами). Тому, застосувавши теорему косинусів до ∆АСД, одержимо , звідки .

Підставивши дані, знайдемо значення .

Підставивши в формулу (2) значення , визначи­мо індукцію магнітного поля.

B=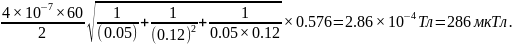

Відповідь: В=286 мкТл

Задача 3

Рамка зі сторонами а=3 см і в=2 см має 400 витків і перебуває в магнітному полі напруженістю 16×10⁴ А/м. По рамці тече струм 10^-7 А. Визначити магнітний момент рамки і обертальний мо­мент, який діє на неї з боку поля, якщо площина рамки утворює кут 60° з напрямком Н.

Дано: Розв’язання

а=3см=0,03м Магнітний момент рамки із струмом:

в=2см=0,02м де S=aв— площа рамки, N — число витків рамки. Звідси ,

N=400

H= Обертальний момент, який діє на рамку із струмом

з боку магнітного поля, ,

де В — індукція магнітного поля, В= Н; кут між

Знайти:

напрямком індукції B магнітного поля і магнітним моментом рамки зі струмом . Тоді ; Перевіримо найменування фізичних величин, які потрібно визначити.

Підставляючи числові значення у формули (1) і (2) і враховую­чи, що Гн/м, одержуємо:

;

Відповідь: ,

Задача 4

Два нескінченно довгих провідники схрещені під прямим кутом По них протікають струми 80 і 60 А. Відстань між провідниками дорівнює 10 см. Визначте магнітну індукцію в точці А, однаково віддалену від обох провідників.

Д ано: Розв’язання

Відповідно до принципу суперпозиції маг­нітних подів 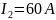магнітна індукція поля, створюваного струмами,

d =10см=0,1м визначається виразом , де і - магнітні

В -? індукції полів, створювані в точці А струмами та відповідно.

Вектори і , взаємно перпендикулярні, то модуль вектора магнітної індукції поля можна визначити за теоремою Піфагора:

та визначаються за формулам розрахунку магнітнітної індукції поля, створюваного нескінченно довгим прямолініним провідником струмом:

і

У даному випадку Тоді

Виконуємо обчислення:

Відповідь:

Задача 5

По двох паралельних проводах, що перебувають у вакуумі на відстані r=10см один від одного, проходять у протилежних напрямках струми, сили яких . Визначити індукцію магнітного поля в точці А, віддаленій на відстань від першого провода і на 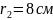від другого, і в точці С, віддаленій відповідно на .

Д ано: Розв’язання

r=10см=0,1м Напрямки векторів магнітної індукції і у точці А,

також і у точці С, визначаємо за правилом

правого гвинта. Згідно з принципом суперпозиції,

магнітна індукція індукція в точці А становить

Вектори і мають однакові напрями, тому модуль

вектора дорівнює сумі модулів векторів і .

Ураховуючі, що

У точці С результуючий- вектор магнітної індукції є діагонал­лю відповідного прямокутника, оскільки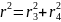 ;. (Загалом при інших відстанях результуючий вектор індукції є діагоналлю парале­лограма, побудованого на векторах, ще додаються, як на сторонах) Модуль вектора-магнітної індукції знайдемо за теоремою Піфагора:

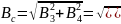
Оскільки 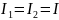, то

Відповідь:

Задача 6

По горизонтально розміщеному провіднику завдовжки 20 см і масою 4 г протікає струм силою 10 А. Знайти індукцію магнітного поля, в яке потрібно помістити провідник, щоб він перебував у рівновазі.

Д ано: Розв’язок

l=20см=0,2м На провідник діє сила тяжіння, направлена вертикально

I =10 A вниз. Цю силу може зрівнО важити сила Ампера, з якою m=4г=4 магнітне поле діє на провідник зі струмом, тобто:

В - ? З формули знайдемо силу Ампера:

. Тоді: .

Обчислення

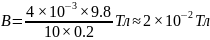
Відповідь:

Задача 7

Плоска прямокутна котушка, сторони якої до­рівнюють 10 см і 5 см, має 200 витків і перебуває в однорідно­му магнітному полі з індукцією 0,05 Тл. Який максимальний обертальний момент може діяти на котушку в цьому полі, якщо сила струму в котушці 2 А?

Д ано: Розв’язання

N=200 Максимальний обертальний момент, який у магнітному полі a=10см=0,1м діє на котушку зі струмом, , де N – кількість

b=5см=0,05м витків у котушці; S- площа одного витка, S=ab. Тоді:

B=0.05Тл

I=2A Обчислення:

Відповідь:

Задача 8

Прямокутна рамка зі струмом розташована в магнітному полі паралельно лініям магнітної індукції. На рамку діє обертальний момент М = 10¹Нм. Визначити роботу, яку необхідно виконати, щоб обернути рамку на кут а=30 відносно осі, що збігається з площиною рамки.

Д ано: Розв'язання

М = 10²Н м

А=30

А - ?

Робота сил поля під час руху рамки зі струмом визначається формулою

А=І(ф₁-ф₂).

де Ф₁ та Ф₂ - потоки через поверхню рамки відповідно при ₁=90 та ₂=60 . Магнітний потік визначається за формулою:

Ф=BScos

Якщо рамка розміщена паралельно лініям індукції поля, то нормаль до площини рамки утворює з вектором кут = 90

тому Ф₁=BScos =0

Якщо рамка обернеться на кут а =30°, то кут між нормаллю і вектором В дорівнюватиме ₂ =60°,

тому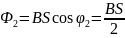

Тоді

Обертальний момент, який діє на рамку зі струмом в її початковому положенні, дорівнює

звідки

Отже, робота сил поля А = I(Ф₂– Ф₁) =

Після обчислення за цією формулою А= 5 • 10^-3 Дж.

Відповідь: А=5 • 10^-3 Дж.

Задача 9

Електрон, маючи дуже малу початкову швидкість, пройшов прискорючу напругу U= 1000 В і влетів в однорідне магнітне поле індукцією B=10² Тл у напрямку, перпендикулярному до вектора напруженості прискорючого електричного поля. Яка буде траєкторія руху електрона?

Д ано: Розв'язання

U=1000 B

B=10²Тл

R-?

1. Визначимо радіус траєкторії руху електрона.

На електрон, який знаходиться у магнітному полі, діє сила Лоренца

Де - швидкість електрона,

- кут між векторами і

Як видно з рис. 6, ця сила перпендикулярна до напрямку швидкості електрона, тому вона надає йому нормального (доцентрового) прискорення

Отже, доцентрова сила, яка діє на електрон, дорівнює

Тоді

Швидкість руху електрона визначимо виходячи з того, шо електрон під дією

напруги , набув певної кінетичної енергії ,тоді

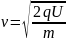
Звідси

Отже траєкторія руху електрона дійсно коло радіусом м.

Відповідь: м

Задача 10

Протон, що пройшов прискорювальну різницю потенціалів 600 В, влетів в однорідна магнітне поле з, індукцією 0,3 Тл почав рухатися по колу. Визначте радіус кола.

Розв'язання

Рух зарядженої частинки в однорідному магнітному полі буде відбуватися по колу тільки в том випадку, коли частинка влітає в магнітне поле перпендикулярне лініям магнітної індукції. При цьому сила Лоренца, спрямована до центра кола, надає протону нормальне прискорення. Відповідно до другого закону Ньютона

Д ано:

U=600 B

B=0,3Тл

R-?

,

Де - маса протона; - нормальне прискорення.

Сила Лоренца визначається виразом

Оскільки вектори магнітної індукції швидкості протона взаємноперпендикулярні, то =90°, .

Тоді

Звідси знаходимо радіус кола

Для визначення швидкості протона скористаємося зв'язком між роботою сил електростатичного поля та зміною кінетичної енергії фотона, тобто

Оскільки то

Одержуємо кінцеву формулу для визначення радіуса кола:

Виконуємо обчислення:

м.

Задача 11

Частинка масою т, що має заряд q, влітає зі швидкістю в однорідне магнітне поле, індукція якого В, під кутом α до лінії магнітної індукції. Визначити траєкторію руху частинки.

Розв’язання

Д ано: m q v B α h -?

Розкладемо вектор швидкості v на дві складо­ві: спрямовану вздовж ліній магні гної індукції, і , пер­пендикулярну до цих ліній. Модулі цих складових відповідно і На частинку діє сила Лоренца, зумовлена складовою У ре­зультаті цього частинка рухається по колу зі швидкістю , , у площині, перпендикулярній до вектора В. Радіус нього кола визначимо, склавши рівняння, згідно і другим законом Ньютона: , або Звідси: . Водночас частинка рухається вздовж поля. Цей рух є рівномір­ним зі швидкістю оскільки складова не зумовлює виникнення сили Лоренца. Отже, якщо частинка рухається одночасно по колу і прямій, вона рухатиметься по гвинтовій лінії, «накручуючись» на лі­нії магнітної індукції. Крок гвинтової лінії становить: , де Т- період обертання частинки по колу

Задача 12

В області простору створено однорідне електростатичне поле Е=10000 В/см, спрямоване вздовж осі Ох, а також одно­рідне магнітне поле В, спрямоване вздовж осі Оу. Через цю область у напрямку осі Оz по прямій лінії рухається пучок мезонів зі швидкістю с/3. Чому дорівнює індукція магнітного поля? Чи можливо за допомо­гою такого експерименту визначити знак заряду мезона? Релятивістським ефектом знехтувати.

Д ано: Розв’язання

Е=10000 В/см=

=

B-?

Якщо вважати заряд мезона пози­тивним, то за правилом лівої руки сила Лоренца спрямована проти осі Ох. За умовою рівномірного прямолі­нійного руху У проекціях на вісь Ох ; Обчислення

Якщо мезони мають негативний заряд, і змінять напрямок на протилежний. Визначити знак заряду мезонів у цьому експерименті неможливо, оскільки заряд не входить до умови рівноваги (скорочується).

Відповідь: В = 10 мТл.

Задача 13

Два паралельних довгих провідника знаходяться на відста­ні 1 м один від одного. В кожному з них тече струм 50 А в од­ному напрямку. Визначити силу тиску проводів на ізолятор, який роз’єднує їх, якщо довжина ізолятора 0,8 м, а µ= 1.

Д ано: Розв’язання

Сила взаємодії паралельних струмів на одиницю їх довжини , ; Обчислення:

I=50 A

r=0.1м

l=0.8м

L=1м

µ= 1

Відповідь:

Задача 14

Протон та електрон влітають в однорідне магнітне поле з одна­ковою швидкістю, перпендикулярно до вектора магнітної індукції. У скільки разів радіус кривизни траєкторії руху протона R_п більший за радіус кривизни траєкторії руху електрона R_е?

Д ано:

Розв’язання Зобразимо рух заряджених частинок у магнітному полі з урахуванням правила лівої руки. На рухому заряджену частинку сила Лоренца, модуль якої В даному випадку Тобто на протон та електрон діють од­накові за модулем сили Лоренца . Ці сили Лоренца відіграють роль доцентрових сил оскільки та збігаються за на­прямком. Виконавши підстановку мо­дуля сили Лоренца та доцентрового прискорення, отримаємо: Виразимо радіус кола Застосуємо цю формулу для протона та електрона Звідси Обчислення Відповідь: