Лабораторная работа №1

Модель межотраслевого баланса Леонтьева

Вычисление совокупного выпуска по заданному спросу

 

Межотраслевой баланс в экономике, как известно, - это метод анализа взаимосвязей между различными секторами экономической системы.

Предположим, что исследуемую экономическую систему можно разделить на несколько отраслей, производящих определенные товары и услуги. При производстве товаров и услуг в каждой отрасли расходуются определенные ресурсы, которые производятся как в других отраслях, так и в данной отрасли. Это означает, что каждая отрасль экономики выступает в системе межотраслевых связей одновременно производителем и потребителем.

Цель балансового анализа - определить, сколько продукции должна произвести каждая отрасль для того, чтобы удовлетворить все потребности экономической системы в его продукции.

Рассмотрим открытую систему межотраслевых связей, в которой вся произведенная продукция (совокупный продукт) разделяется на две части: одна часть продукции (промежуточный продукт) идет на потребление в производящих отраслях, а другая ее часть (конечный продукт) потребляется вне сферы материального производства - в секторе конечного спроса; при этом потребление в секторе конечного спроса может меняться.

Обозначим:

- объем выпуска i-го сектора, валовой выпуск (объем товаров и услуг, произведенных в одном из n производящих секторов), i=1,2,...,n;

- объем товаров и услуг i-го сектора, потребляемых в j-ом секторе (межотраслевые поставки);

- конечный продукт i-го сектора (объем продукции i-го сектора, потребляемой в секторе конечного спроса);

- количество продукции i-го сектора, которое расходуется при производстве одной единицы продукции j-го сектора (коэффициенты прямых затрат).

При этом межотраслевые поставки можно найти по формуле

Промежуточное потребление – это суммарный объем продукции i-го сектора ,используемый во всех остальных секторах:

Промежуточные затраты- это затраты j-го сектора на закупку продукции остальных отраслей, необходимой для производства :

Валовая добавленная стоимость (условно чистая продукция):

,

Межотраслевой баланс - это равенство объема выпуска каждого производящего сектора суммарному объему его продукции, потребляемой производственными секторами и сектором конечного спроса. В приведенных обозначениях имеем соотношения баланса:

, i=1,2,...,n.

Соотношения баланса, записанные через коэффициенты прямых затрат, имеют вид:

, i=1,2,...,n,

или, что то же самое,

, i=1,2,...,n.

Последние равенства описывают технологию производства и структуру экономических связей и означают, что в сектор конечного спроса от каждого производственного сектора поступает та часть произведенной продукции, которая остается после того, как обеспечены потребности производящих секторов.

Если обозначить вектор выпуска через X, вектор спроса (вектор конечного продукта) - через Y, а технологическую матрицу экономики - матрицу, элементами которой являются коэффициенты прямых затрат , через А, то соотношения баланса в матричной форме будут иметь вид: , где Е - единичная матрица.

Одна из основных задач межотраслевого баланса - найти при заданной структурной матрице А экономической системы в условиях баланса совокупный выпуск X, необходимый для удовлетворения заданного спроса Y.

Если матрица обратима, то решение такой задачи определяется как .

Матрица называется матрицей полных затрат.

Основные соотношения межотраслевого баланса обычно оформляются в виде таблицы ,которая называется схемой межотраслевого баланса .

Пример.

Задана модель экономики, в которой выделены четыре сектора: три производящих сектора (промышленность, сельское хозяйство, транспорт) и домашние хозяйства в качестве сектора конечного спроса. Структура экономики описана в таблице (объемы указаны в единицах стоимости). В первых трех столбцах и трех первых строках представлены межотраслевые поставки . В четвертом столбце вектор конечного спроса, в пятом столбце валовой выпуск:

	Сельское хозяйство	Промышленность	Транспорт	Домашние хозяйства	Общий выпуск
Сельское хозяйство	400	300	200	250	1150
Промышленность	250	300	160	530	1240
Транспорт	100	450	120	400	1070

Схема межотраслевого баланса в этом случае будет иметь вид:

Задания для лабораторной работы №1 Задание №1

Исследуйте заданную таблицей модель экономической системы за отчетный период (в таблицах А и I – сельское хозяйство, В и II – промышленность, С и III – транспорт, IV – сектор конечного спроса (домашние хозяйства), V – общий выпуск).

1. Постройте схему межотраслевого баланса за отчетный период.

2. Вычислите коэффициенты прямых затрат по формуле 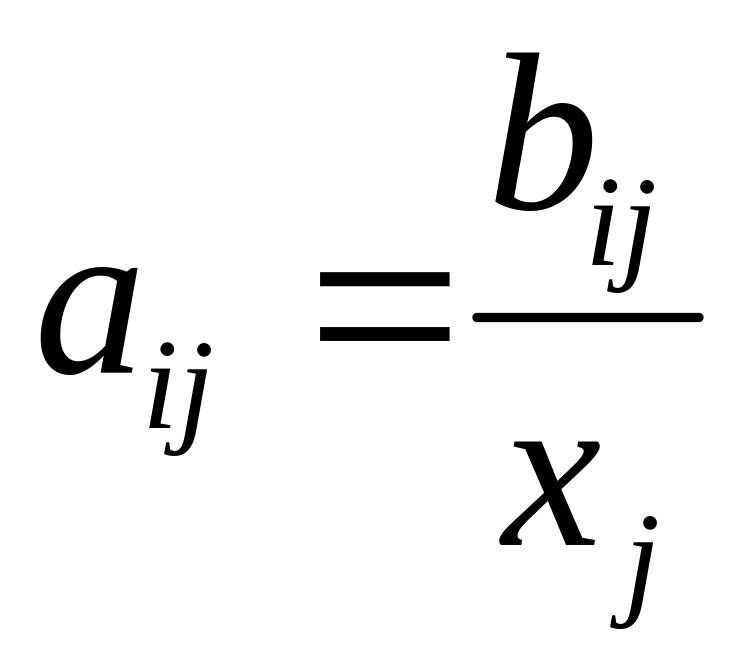. Матрица - технологическая матрица (матрица прямых затрат)

3. Проверьте продуктивность матрицы А.

4. Вычислите матрицу полных затрат D.

5. Определите по формуле ,

каким должен быть валовой выпуск продукции отраслей в плановом периоде, если задан предполагаемый вектор конечного спроса Y .

6. Составить схему межотраслевого баланса для планового периода с заданным вектором конечного спроса Y.

Варианты заданий

№1 Y=(100 100 110)

	I	II	III	IV	V
A	10	16	50	20	96
B	3	15	40	23	81
C	2	26	30	32	90

№2 Y=(110 100 100)

	I	II	III	IV	V
A	15	16	55	20	106
B	10	15	43	23	91
C	2	21	27	30	80

№3. Y=(100 120 110)

	I	II	III	IV	V
A	5	16	40	15	76
B	5	15	40	20	80
C	10	28	30	32	100

№4. Y=(130 100 120)

	I	II	III	IV	V
A	30	10	56	20	116
B	6	12	46	20	84
C	5	21	27	32	85

№5. Y=(125 100 110)

	I	II	III	IV	V
A	10	18	51	19	98
B	8	10	40	28	86
C	7	26	30	32	95

№6. Y=(100 140 110)

	I	II	III	IV	V
A	7	16	50	20	93
B	3	10	45	28	86
C	2	26	30	32	90

№7. Y=(150 100 110)

	I	II	III	IV	V
A	10	20	50	20	100
B	3	15	40	23	81
C	2	26	37	32	97

№8. Y=(100 130 130)

	I	II	III	IV	V
A	5	11	55	25	96
B	3	15	41	23	82
C	4	26	30	32	92

.

№9. Y=(110 120 110)

	I	II	III	IV	V
A	15	26	25	30	96
B	10	15	40	23	88
C	2	26	30	32	90

№10. Y=(130 120 110)

	I	II	III	IV	V
A	10	16	50	20	96
B	8	10	60	23	101
C	2	26	30	32	90