3. Матричные игры

3.1. Принцип максимина; решение игры в чистых стратегиях

Теория игр обосновывает выбор принципов оптимальности поведения игроков и разрабатывает алгоритмы нахождения оптимальных стратегий и выигрышей игроков. Признаками игровой ситуации являются: наличие конфликта интересов, неполнота и неопределенность информации. Такие условия вынуждают участника игры действовать по логике расчета на наихудшую реализацию неизвестных условий, выбирая из наихудших реализаций лучшую. В качестве принципа оптимальности поведения игроков в матричных играх, выработанного теорией игр, служит принцип устойчивости, когда отклонение от оптимального поведения невыгодно ни одному игроку при условии, что другой действует оптимальным образом.

П о определению (14) платежная функция матричной игры задается в виде матрицы , элемент которой есть выигрыш первого игрока при условии, что первый игрок (игрок А) выбрал стратегию i из набора возможных стратегий А_i , , а второй игрок (игрок В) выбрал стратегию j из набора возможных стратегий В_j, :

	j i	В1 . . .	Вj	. . .Вn
А=	А1 . . .
	Аi		aij
	. . . Ат

Пример 1. Рассмотрим следующую игровую ситуацию: два игрока выбрасывают 1, 2, 3, 4, 5 пальцев руки. Если сумма нечётная, первый игрок выигрывает сумму очков, равную количеству пальцев, выброшенных обоими игроками; если сумма чётная – второй выигрывает такую же сумму очков.

Решение

Количество стратегий игроков n = m = 5.

Запишем стратегии игроков:

A_i = {игрок А выбросил i пальцев}, ,

B_j = {игрок B выбросил j пальцев}, .

Платежная матрица игры имеет следующий вид:

j i	В1	В 2	В 3	В 4	В 5
А1	-2	3	-4	5	-6
А 2	3	-4	5	-6	7
А 3	-4	5	-6	7	-8
А 4	5	-6	7	-8	9
А 5	-6	7	-8	9	-10

Опишем логику поведения игроков, учитывая антагонизм интересов игроков, вынуждающий каждого из них рассчитывать на сильное противодействие другого. Первый игрок старается максимизировать свой выигрыш в условиях неопределённости, создаваемой антагонистическими действиями второго игрока. В этом случае игрок А для каждой своей стратегии i определяет свой гарантированный выигрыш, т.е. выигрыш в худшей для себя ситуации

.

Т.к. выбор любой стратегии в его распоряжении, чтобы максимизировать свой гарантированный выигрыш игрок А из гарантированных выигрышей по стратегиям выбирает максимальный:

(1)

Определение 18. Величина , вычисленная по (1), называется нижней чистой ценой игры и интерпретируется как максимальный гарантированный выигрыш А; стратегия , при которой выполняется (1), называется максиминной стратегией.

Определим нижнюю чистую цену игры и максиминные стратегии для примера 1:

максиминные стратегии - А₁, А₂.

Второй игрок старается минимизировать свой проигрыш в условиях противодействия игрока А. Поэтому игрок В для каждой своей стратегии j определяет свой гарантированный проигрыш, т.е. то, что он вынужден будет заплатить при самом неблагоприятном поведении А:

.

Т.к. он волен выбирать любую свою стратегию, он, естественно, выбирает ту, что минимизирует его проигрыш:

. (2)

Определение 19. Величина β, рассчитанная по (2), называется верхней чистой ценой игры и интерпретируется как минимальный гарантированный проигрыш В; cтратегия , при которой выполняется (2), называется минимаксной стратегией.

Определим верхнюю чистую цену игры и минимаксные стратегии для примера 1:

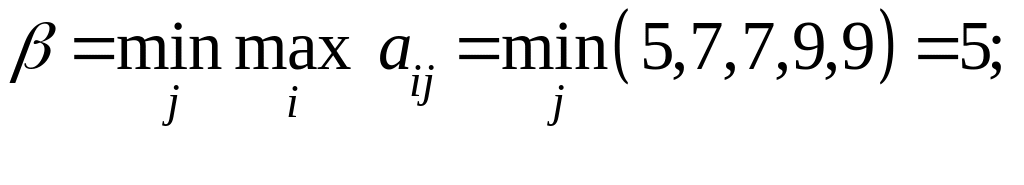минимаксная стратегия - В₁.

Определение 20. Решением игры называется процесс нахождения оптимальных стратегий игроков и цены игры и ценой матричной игры называется выигрыш игрока А (или проигрыш В).

Определение 21. Если для чистых максиминной и минимаксной стратегий выполняется равенство α = β при и , то:

• стратегии и называются уравновешивающей парой и являются оптимальными стратегиями;

• точка (i_о, j_о) называется седловой точкой;

• элемент называется седловым элементом и является ценой игры.

Пусть игроки А и В в матричной игре с платёжной матрицей могут выбирать одну из стратегий совокупности {A_i} или {B_j}. Пусть p_i, q_j вероятности того, что игрок А выберет A_i, а игрок В - B_j. Тогда, учитывая, что набор стратегий представляет собой полную группу событий, имеют место условия нормировки:

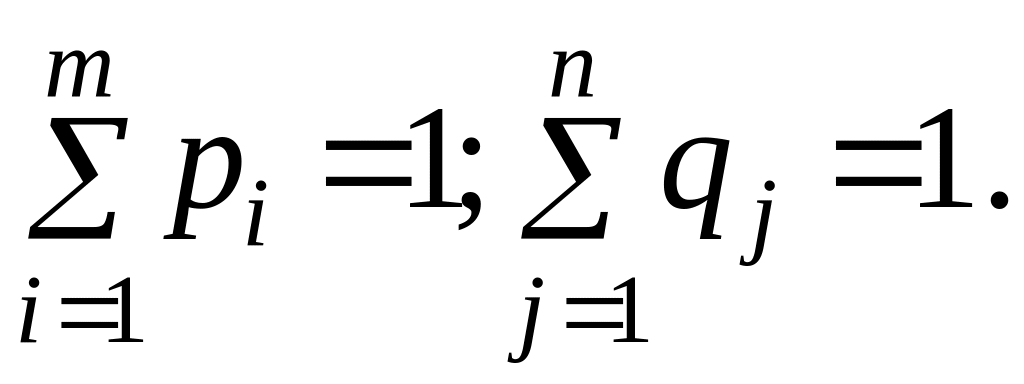
Образуем векторы и следующим образом: если А выбрал стратегию A_i, то ; если В выбрал стратегию B_j, то .

Определение 22. Вектора и , описывающие выбор стратегий игроками А и В, называются стратегиями игроков; чистая стратегия A_i или B_j – это стратегия, выбранная с вероятностью, равной единице.

Определение 23. Формализованное правило, согласно которому можно определить выигрыш каждого игрока в конкретной ситуации, т.е. в зависимости от стратегии, выбранной данным игроком и остальными участниками игры, называется платежной функцией игры.

Определим платёжную функцию матричной игры по схеме:

1. Введем случайные величины ξ, η такие, что

(3) Здесь Р{с} – вероятность того, что событие с произошло. Соотношения (3) по определению задают законы распределения случайных величин ξ и η.

2. Образуем систему случайных величин ξ и η - (ξ , η) или вектор, компонентами которого являются значения случайных величин ξ и η.

3. Введем функцию системы случайных величин ν такую, что она принимает значение элемента платежной матрицы, если случайная величина ξ=i и случайная величина η=j:

.

Таким образом, значение случайной функции ν есть величина выигрыша игрока А (проигрыша игрока В) при различных стратегиях игроков.

4. Найдем средний выигрыш игрока А как математическое ожидание функции двух случайных аргументов:

. (4) Здесь М[] - математическое ожидание случайной функции .

Игроки А и В выбирают стратегии тайно и независимо друг от друга, следовательно, случайные величины ξ и η независимы, поэтому можно записать:

.

Тогда (4) запишется в виде

.

Определение 24. Функция вида называется платёжной функцией матричной игры.

Определение 25. Стратегии и называются оптимальными, если для каждой стратегии игроков – , выполняется условие

. (5)

Условие (5) означает, что при каждой неоптимальной стратегии игрока А его выигрыш не возрастает в сравнении с оптимальным при условии, что игрок В действует оптимальным образом, а при каждой неоптимальной стратегии игрока В его проигрыш не убывает в сравнении с оптимальным.

Примем без доказательства теорему, показывающую связь седловой точки с ценой игры и оптимальными стратегиями.

Теорема 1. Для того чтобы точка (i_0, j₀) была седловой, необходимо и достаточно, чтобы чистые стратегии и или , были оптимальными; при этом цена игры .

Следствие из теоремы 1: если платёжная матрица А имеет седловую точку, то обязательно существуют оптимальные чистые стратегии; если седловой точки нет, то оптимальные стратегии могут быть только смешанными.