Необходимые условия экстремума. Уравнение Эйлера-Лагранжа

Требуется найти минимум функционала

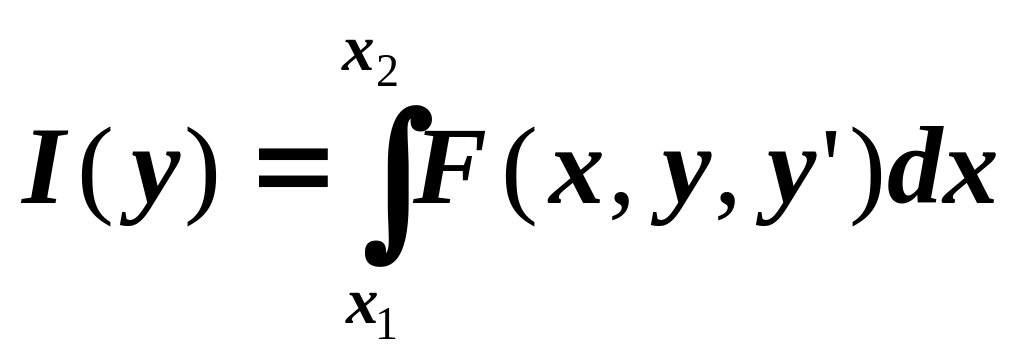(1)

среди кусочно-гладких линий, соединяющих точки y(x₁) = y₁ и y(x₂) =y₂, .

Считая, что функция y=y(x) доставляет локальный минимум функционалу, находят условия, которым y=y(x) должна удовлетворять.

Первая и вторая вариации функционала. Если произвольная кусочно-гладкая функция, удовлетворяющая условиям , то однопараметрическое семейство функций

при достаточно малых значениях параметра, принадлежит некоторой окрестности функции y=y(x). Функционал

на указанном однопараметрическом семействе функций является функцией параметра α

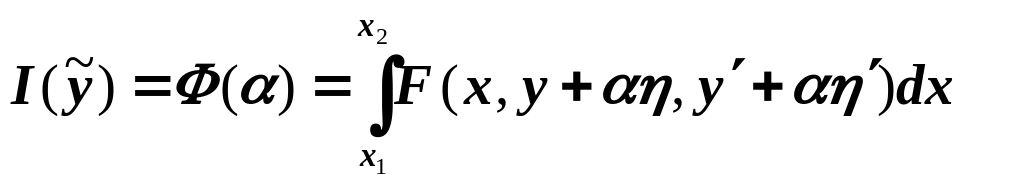
имеющей минимум при α=0.

В силу необходимых условий минимума функции имеем: , .

Дифференцирование по параметру дает:

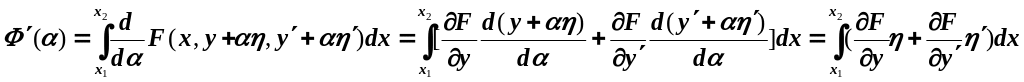
(задание на дом: найти выражение для )

Проинтегрируем второй член по частям:

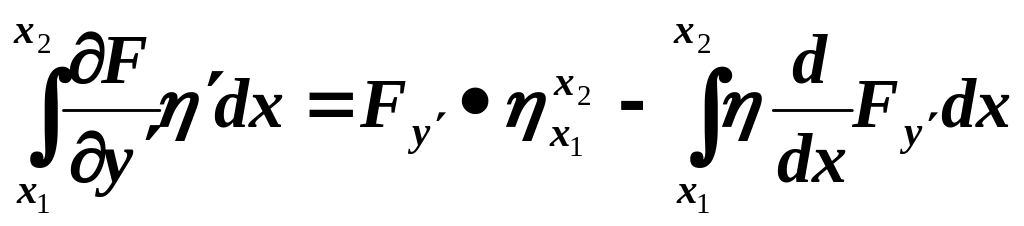и т.к.

(2)

Производная функции в точке α=0 называется первой вариацией функционала (3.1) и обозначается символом :

|

Вторая вариация функционала (1) определяется как вторая производная функции в точке α=0

|

Необходимые условия минимума (максимума) функционала (1):

1. Первая вариация должна обращаться в нуль: =0

2. Вторая вариация должна быть в случае минимума неотрицательной, а в случае максимума неположительной: ≤0.

Применяя к выражению (2) лемму Дюбуа-Реймона о том, что из соотношения ортогональности:

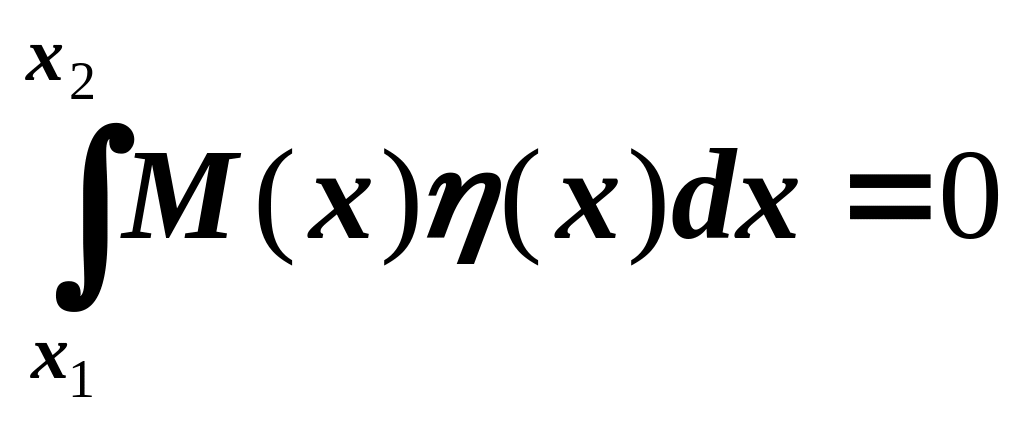
где M(x) кусочно-непрерывная, а η(x) – произвольная кусочно-гладкая функция, следует, что M(x)=0, получим уравнение Эйлера-Лагранжа в дифференциальной форме:

, (3)

которое является первым необходимым условием экстремума функционала .

Рассмотрим три частных случая для уравнения (3).

1. F не зависит от y, т.е. 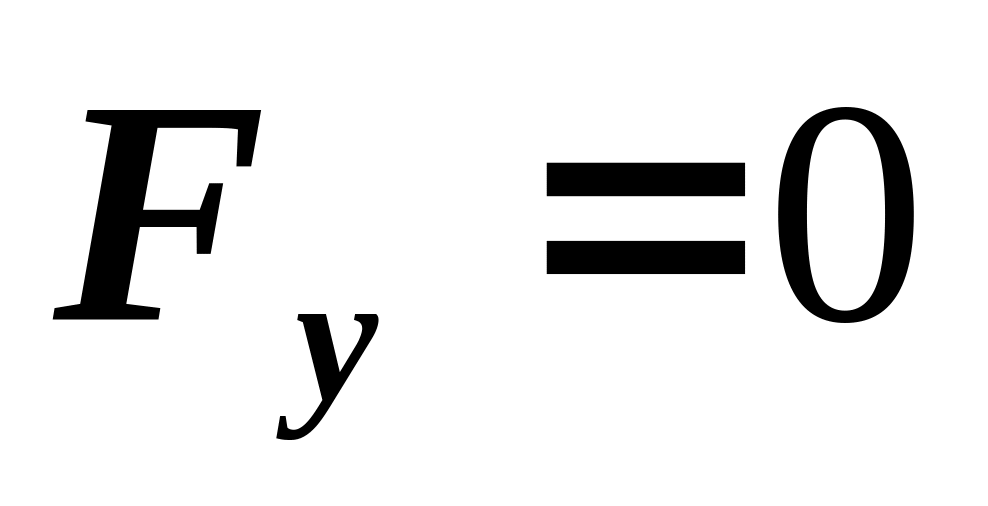, тогда 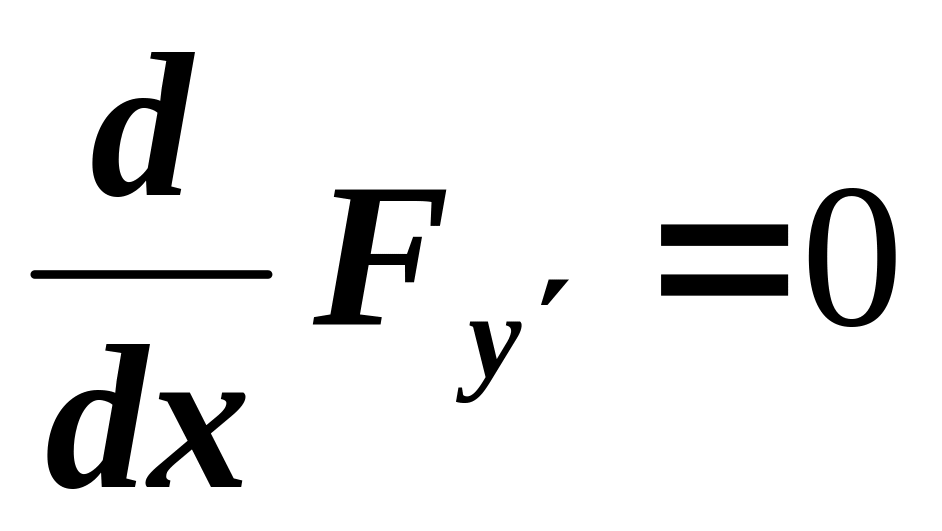и, следовательно,

Из последнего уравнения можно определить как функцию x и затем – искомую функцию как интеграл от этого решения.

2. , т.е. F не зависит явно от x. Заметим, что выражение

в этом случае принимает вид

а уравнение Эйлера-Лагранжа

Умножив обе части уравнения на получим

откуда .

Это уравнение принято называть первым интегралом Эйлера.

3. Допустим, что F зависит только от . В этом случае уравнение Эйлера-Лагранжа принимает вид:

,

следовательно, =const = k, и уравнения экстремалей запишутся как

y = kx + b

т.е. экстремали будут прямыми линиями.

Общее решение уравнения Эйлера-Лагранжа содержит две неопределенные постоянные, для определения которых требуется удовлетворение двум условиям. Как правило, в качестве таких условий задаются значения функции y(x) в начале и конце интервала y(x₁) и y(x₂).

Таким образом, экстремальная задача сводится к решению нелинейного дифференциального уравнения 2-го порядка с переменными параметрами, т.к. в общем случае функция F нелинейна относительно y и y' и поэтому решить его не удается. Кроме того, для справедливости этого уравнения требуется непрерывность как первой, так и второй производных функции y(x), что не дает возможности рассматривать очень важные для приложений функции управления в виде ступенчатых кривых с насыщением (кусочно-постоянных). Такая возможность появляется с применением принципа максимума Понтрягина и метода динамического программирования Беллмана.

Рассмотрим теперь два классических примера на применение уравнения Эйлера-Лагранжа.

Пример 1. Задача о длине кривой.

и следовательно, уравнение Эйлера имеет вид: т.е. y”=0

и y = C₁ x + C₂ – это уравнение прямой, т.е. как и следовало ожидать, минимальное расстояние между двумя точками есть прямая линия.

Пример 2. Задача о брахистохроне (линии наискорейшего спуска). Задача поставлена Иоганном Бернулли в 1696 г. (1-е решение – Якоб Бернулли, 2-е – Лопиталь, 3-е – Ньютон).

Длина ; скорость

Найти экстремали функционала

Подинтегральная функция явно от x не зависит, поэтому воспользуемся первым интегралом Эйлера .

; ;

Подстановка дает

Таким образом в параметрическом виде экстремаль задается уравнениями . Это циклоиды.