
Алгоритм обучения нейронной сети с учителем:
-
Инициализируем элементы весовой матрицы небольшими случайными значениями. У нас в матрицу входит два коэффициента
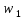 и
и
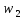 .
Берём
.
Берём
 и
и
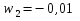 .
. -
Подать на входы один из входных векторов, которые сеть должна научиться различать и вычислить её выходы. Выход вычисляется по формуле
 ,
где
,
где
 и
и
 -
заданные по условию в таблице координаты
образа (вектора)
-
заданные по условию в таблице координаты
образа (вектора) .
В нашем случае изначально берем
.
В нашем случае изначально берем
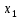 и
и
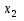 по порядку из таблицы, т.е. для для
образа
по порядку из таблицы, т.е. для для
образа
 .
.
-
Проверяем равильность выходного сигнала. Правильность проверяется по отношению к эталонному значению
 .
Выход
.
Выход
 будет
считаться правильным, если
будет
считаться правильным, если
 .
Так как идеально получиться не может,
нас устроит небольшая погрешность,
т.е.
.
Так как идеально получиться не может,
нас устроит небольшая погрешность,
т.е.

Если выход правильный, перейти к шагу 4.
Иначе
(если выход неправильный, т.е.
![]() )
вычислить разницу между идеальным и
полученным значениями выхода
)
вычислить разницу между идеальным и
полученным значениями выхода
![]() и
модифицировать веса в соответствии с
формулой дельта-правила:
и
модифицировать веса в соответствии с
формулой дельта-правила:
![]() .
.
В
нашем случае
![]() или
или
![]() ,
,
![]() (задано)
(задано)
Получается
следующее:
если
![]() , то
весовые
коэффициенты будут увеличены и тем
самым уменьшат ошибку. В противном
случае они будут уменьшены, и
, то
весовые
коэффициенты будут увеличены и тем
самым уменьшат ошибку. В противном
случае они будут уменьшены, и
![]() тоже уменьшится, приближаясь к
тоже уменьшится, приближаясь к
![]() -
уменьшится ошибка.
Отметим,
что
-
уменьшится ошибка.
Отметим,
что
![]() и
и
![]() модифицируются одновременно. Проделываем
модификацию до тех пор, пока нужная нам
точность не будет достигнута.
модифицируются одновременно. Проделываем
модификацию до тех пор, пока нужная нам
точность не будет достигнута.
-
Продолжаем подавать на входы нейронной сети векторы в заданном по условию (в таблице) порядке, но уже используя полученные на шаге 3. значения
 и
и
 .
"Прогнав" через входы сети все
данные по условию векторы (10 векторов),
т.е. обучающую последовательность, мы
в итоге получим интересующие нас
значения коэффициентов
.
"Прогнав" через входы сети все
данные по условию векторы (10 векторов),
т.е. обучающую последовательность, мы
в итоге получим интересующие нас
значения коэффициентов
 и
и
 .
.
Получив
коэффициенты
![]() и
и
![]() ,
мы получили угол наклона нужной нам
прямой (гиперплоскости).
,
мы получили угол наклона нужной нам
прямой (гиперплоскости).
Вычислим
значения
![]() для каждого из заданных по условию
векторов.
для каждого из заданных по условию
векторов.
Воспользовавшись
формулой
![]() ,
найдём
,
найдём
![]() как
среднее значение всех полученных ранее
как
среднее значение всех полученных ранее
![]() ,
т.е.
,
т.е.
 .
.
Занесем найденные коэффициенты в Таблицу 5:
-

0,70086

0,08616

0,06616
Таблица 5
На
основе этих коэффициентов, используя
формулу
![]() ,
построим разделяющую гиперплоскость
на Рис.1. На этом же Рис.1 отобразим
распределение образов в Евклидовом
пространстве:
,
построим разделяющую гиперплоскость
на Рис.1. На этом же Рис.1 отобразим
распределение образов в Евклидовом
пространстве:
Р ис.1
ис.1
Из
Рис.1 видно, что
![]() и
и
![]() относятся
к классу "1", а
относятся
к классу "1", а
![]() к классу "0".
к классу "0".
Ответ:
![]() и
и
![]() относятся
к классу "1", а
относятся
к классу "1", а
![]() к классу "0".
к классу "0".
