Решение

Задаем значения и заносим их в Таблицу 1:

	5	5
	8	4
	2	2

Таблица 1

Для решения задачи любым из предложенных способов нам понадобятся следующие формулы:

(скалярное умножение векторов);

- абсолютное значение вектора (норма).

Во всех случаях нас интересует минимальное расстояние.

а) Для Евклидова расстояния используем формулу:

Получим:

	Евклидово расстояние
	3,16227767
	4,24264069

Таблица 2

Образ "ближе" к .

б) Для направляющих косинусов используем формулу:

Получим:

	Направляющие косинусы
для	0,9486833
для	1

Таблица 3

Образ "ближе" к .

в) Для расстояния Танимото используем формулу:

Получим:

	Расстояние Танимото
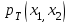
	0,857142857
	0,526315789

Таблица 4

Образ "ближе" к .

Ответ: При использовании метрик Евклидова расстояния и направляющих косинусов браз "ближе" к , при использовании метрики расстояния Танимото образ "ближе" к .

2.2. Задана обучающая последовательность, характеризующая некоторое распределение образов на два класса.

Задать произвольно (в диапазоне значений 0 - 10 ) три "своих" образа (, ,).

Определить, к каким классам относятся заданные три вектора.

а) Решить задачу с применением методов ближайшего соседа и сравнения с эталоном (при этом использовать метрику Евклидова расстояния).

б) Решить задачу с использованием метода линейной разделяющей функции и одного из алгоритмов обучения.

Исходные данные и результаты свести в таблицу.

Отобразить распределение образов в Евклидовом пространстве (на плоскости).

Сделать выводы

Решение

(при решении задачи будем использовать MS Excel)

Задаем три "своих" образа и заносим их в Таблицу 1 :

Талица 1

			Класс	Метод ближай- шего соседа	Метод сравнения с эталоном	Метод линейного разделения
	4	1	0
	2	1	0
	5	2	0
	1	2	0
	1	3	0
	7	3	1
	9	4	1
	7	4	1
	6	5	1
	7	6	1
-	7	2	-----	1	1	1
-	3	3	-----	0	0	0
-	2	9	-----	1	1	1

а)

Метод ближайшего соседа:

При решении задачи классификации методом ближайшего соседа необходимо каждый "свой" образ сравнивать со всеми образами обучающей последовательности.

	3,16227766	2,236068	8,24621125
	5,099019514	2,236068	8
	2	2,236068	7,61577311
	6	2,236068	7,07106781
	6,08276253	2	6,08276253
	1	4	7,81024968
	2,828427125	6,082763	8,60232527
	2	4,123106	7,07106781
	3,16227766	3,605551	5,66
	4	5	5,83

Таблица 2

Получаем, что и относятся к классу "1", а к классу "0".

Метод сравнения с эталоном:

При решении задачи классификации методом сравнения с эталоном, необходимо сначала вычислить этот эталон (т.е. найти среднее по каждой из координат).

Вычислим эталоны для каждого класса:

Класс "0"		Класс "1"
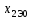
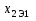
2,6	1,8	7,2	4,4

Таблица 3

Далее для каждого "неклассифицированного" объекта вычислим расстояние до эталона, используя метрику Евклидова расстояния:

	До эталона класса " 0"	До эталона класса "1"
	4,404543109	2,408319
	1,264911064	4,427189
	7,224956747	6,942622

Таблица 4

Получаем, что и относятся к классу "1", а к классу "0".

б)

При решении задачи классификации методом линейной разделяющей функции необходимо «построить» разделяющую линию, т.е. найти коэффициенты _.

, где

- i-информационный признак;

-коэффициент соответствующего признака.

У нас , т.е формула гиперплоскости сводится в двухмерном пространстве к прямой .

Для нахождения коэффициентов и воспользуемся алгоритмом обучения нейронной сети с учителем, основанном на правиле Розенблатта (дельта-правило).

Дельта()-правило: , где

- эталонное значение выходного сигнала нейрона (Если поданный на вход сети вектор относится к классу "0", то . Если к классу "1", );

- коэффициент скорости обучения , ;

и - номера соответственно текущей и следующей итераций;

- номер входа.