2. Системи лінійних алгебраїчних рівнянь

Для розв’язування системи лінійних рівнянь створені потужні матричні методи, які описані у відповідних монографіях та довідниках. Функція solve системи Maple може бути також використана для отримання розв’язку системи лінійних алгебраїчних рівнянь. Такий метод в багатьох випадках може виявитись вдалим. Для розв’язування система рівнянь та перелік невідомих задаються у вигляді множин, як це показує приклад двох рівнянь

> eq1:= a*x+b*y=e; eq2:= c*x+d*y=f;

solve({eq1,eq2},{x,y});

В цьому прикладі a,b,с,d – постійні коефіцієнти, задані в буквеному вигляді, знак * означає операцію множення, e,f – праві частини рівнянь, а x та y – невідомі. Якщо невідомих та рівнянь інше число, написані операції можуть бути використані аналогічним чином. Як бачимо, розв’язок отримано в символьному (аналітичному) виді.

Тепер зробимо приклад з чисельними значеннями коефіцієнтів біля невідомих та правих частин двох лінійних алгебраїчних рівнянь:

> restart;

eq1:= 4*x1+8*x2=5;

eq2:= 6*x1+2*x2=6;

solve({eq1,eq2});

При записі логічно нових виразів, на початку розв’язування нової задачі необхідно ставити команду restart, що затирає у пам’яті проміжні обчислення попередніх задач, які можуть вплинути негативним чином на розв’язок нової задачі.

Ще одним способом розв’язування систем алгебраїчних рівнянь може бути застосування матричного запису системи та використання команди linsolve з пакету linalg системи Maple.

Підключення пакету виконується записом: with(linalg).

Будь-яку систему лінійних алгебраїчних рівнянь у матричному вигляді можна записати таким чином:

, де

А – матриця коефіцієнтів біля невідомих системи,

Х – вектор змінних,

В – вектор вільних членів.

Матриця задається командою вигляду:

matrix(n,m,[[a11,...,a1m],[a21,…,a2m],…,[an1,an2,…,anm]]), де n задає кількість рядків, m – стовпців, а вирази в квадратних дужках є записами елементів матриці за рядками.

Якщо маємо матрицю з одиничною кількістю рядків чи стовпців, то записуємо:

vector(n,[a1,...,an]).

Нехай нам задана система п’яти рівнянь:

Можемо розв’язати її таким чином:

> with(linalg):

A:=matrix(5,5,[[1,2,1,-3,1],[3,-3,2,3,1],[-1,1,3,-1,6],[2,4,1,2,2], [4,5,2,3,4]]);

> B:=vector(5,[1,3,5,2,4]);

> X:=linsolve(A,B);

Отож ми отримали розв’язок системи рівнянь у вигляді вектору Х.

Цей спосіб є більш зручним і лаконічним, не потребує громіздких записів.

3. Знаходження похідних від функцій

Обчислення n-го порядку похідних від функцій – одна з найбільш поширених задач математичного аналізу. Для її реалізації Maple має декілька основних функцій.

Нехай маємо функцію f(x1, x2, …, xn), що залежить від змінних x1, x2, …, xn.

Знаходження її похідної мовою Maple зводиться до виконання таких команд:

diff(a, x1, x2, …, xn);

Diff(a, x1, x2, …, xn);

diff(a, [x1, x2, …, xn]);

Diff(a, [x1, x2, …, xn]);

У цих командах a – диференційований вираз, наприклад, задана нами функція від змінних x1, x2, …, xn:

Якщо ми маємо функцію f(x,y)=2*x+3*y, тоді замість а підставляємо 2*x+3*y, а замість змінних x1, x2, …, xn – змінну x, змінну y, або ж обидві, відокремлюючи їх комами.

Функція Diff є інертною формою обчислювальної функції diff і застосовується для формалізованого запису похідних у документах. Це означає, що у тих випадках, коли ми хочемо записати вираз, що вказує на те, що ми беремо від нього похідну, ми застосовуємо цю команду, наприклад:

> Diff(f(x),x);

Виведе просто узагальнений вигляд:

Функція diff(a, x1, x2, …, xn) обчислює частинні похідні заданого виразу a за змінними x1, x2, …, xn. У найпростішому випадку diff(f(x), x) обчислює першу похідну функції f(x) за змінною x.

При n, більшому за одиницю, обчислення похідних виконуються рекурсивно, наприклад, diff(f(x), x, y) є еквівалентним до diff(diff(f(x), x), y). Для обчислення похідних вищого порядку застосовують оператор $, що ставлять після імені відповідної змінної, вказуючи після нього порядок похідної. Наприклад, вираз diff(f(x), x$3) обчислює похідну третього порядку.

Знаходження похідних від логарифмічних функцій однієї змінної

1.

> Diff(y(x),x)=diff((1-x^2)^(1/2)*ln(((1-x)/(1+x))^(1/2))+1/2*ln((1-(1-x^2)^(1/2))/(1+(1-x^2)^(1/2)))+(1-x^2)^(1/2),x);

> simplify(%);

2.

> Diff(y(x),x)=diff(log[2](log[3](log[5](x))),x);

> simplify(%);

Знаходження похідних від тригонометричних функцій

3.

> Diff(y(x),x)=diff((x*sin(x))/(1+tan(x)),x);

> simplify(%,size);

> simplify(%,trig);

4.

> Diff(y(x),x)=diff((1+tan(x+1/x))^(1/2),x);

> simplify(%);

5.

> Diff(y(x),x)=diff(sin(cos(tan(x)^3)^2),x);

> simplify(%,trig);

Знаходження похідних від обернених тригонометричних функцій

6.

> Diff(y(x),x)=diff(1/2*(arcsin((x^2+2*x)^(1/2)))^(1/4),x);

> simplify(%,size);

7.

> Diff(y(x),x)=diff(arctan(x-(1+x^2)^(1/2))+arccos((b+a*cos(x))/(a+b*cos(x))),x);

Знаходження похідних від степеневих функцій

8.

> Diff(z(x),x)=diff((x^2+1)/(3*(x^2-1))+(x^2-1)*(1-x),x);

> simplify(%,size);

9.

> Diff(y(x),x)=diff((2/x^(1/2)-sqrt(3))*(4*x*x^(1/3)+x^(2/3)/(3*x)),x);

> simplify(%);

10.

> Diff(y(x),x)=diff(1/(2*x-1)^(1/3)+5/(x^2+2)^(3/4),x);

> simplify(%,size);

Знаходження похідних від показникових функцій

11.

> Diff(y(x),x)=diff((x^3+2^x)/exp(x),x);

> simplify(%,size);

12.

> Diff(y(x),x)=diff(x/4^x,x);

> simplify(%,size);

Знаходження похідних від різних складних функцій

13.

> Diff(y(x),x)=diff(-x/(1+8*x^3)+1/12*ln((1+2*x)^2/(1-2*x+4*x^2)) +sqrt(3)/6*arctan((4*x-1)/sqrt(3)),x);

> simplify(%,size);

> simplify(%,size);

14.

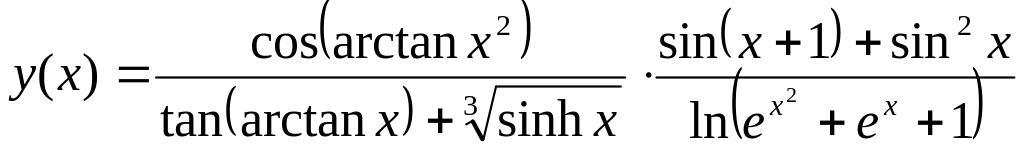
> Diff(y(x),x)=diff(cos(arctan(x^2))/(tan(arctan(x))+sinh(x)^(1/3))* (sin(x+1)+sin(x)^2)/ln(exp(x^2)+exp(x)+1),x);

Похідна від функцій, заданих неявно

14.

> f := y^2 = 2*p*x;

> implicitdiff(f,y,x);

15.

> f := x^2/a^2+y^2/b^2 = 1;

> implicitdiff(f,y,x);

16.

> f := (x^2+y^2)^(1/2) = (x+exp(y)+5)^(1/3);

> implicitdiff(f,y,x);

Застосування пакету student для візуалізації дотичної до функції в точці

Покажемо команди, як провести дотичну до заданої функції в заданій точці.

> with(student):

showtangent(x^2+5, x = 2);

Знаходження похідних від функцій, заданих параметрично

17.

Знайти

> x(t):=(1-sqrt(t))^(1/3);y(t):=sqrt(1-t^(1/3));simplify(diff(y(t), t)/diff(x(t),t));

Знаходження похідних вищих порядків

18.

Знайти

> Diff(y(x),x)=diff(x*(2*x-1)^2*(x+3)^3,x$4);

19.

Знайти

> Diff(y(x),x)=simplify(diff(cos(3*x)/(1-3*x)^(1/3),x$2),size);

Знаходження частинних похідних від функцій,

що залежать від декількох змінних

20.

Знайти частинні похідні першого і другого порядку від заданої функції

> Diff(u(x,y,z),x)=diff(1/sqrt(x^2+y^2+z^2),x); Diff(u(x,y,z),y)=diff(1/sqrt(x^2+y^2+z^2),y);

Diff(u(x,y,z),z)=diff(1/sqrt(x^2+y^2+z^2),z);

> Diff(u(x,y,z),x$2)=simplify(diff(1/sqrt(x^2+y^2+z^2),x$2),size);

Diff(u(x,y,z),y$2)=simplify(diff(1/sqrt(x^2+y^2+z^2),y$2),size);

Diff(u(x,y,z),z$2)=simplify(diff(1/sqrt(x^2+y^2+z^2),z$2),size);

> Diff(u(x,y,z),x,y)=diff(1/sqrt(x^2+y^2+z^2),x,y);

Diff(u(x,y,z),y,z)=diff(1/sqrt(x^2+y^2+z^2),y,z);

Diff(u(x,y,z),x,z)=diff(1/sqrt(x^2+ y^2+z^2),x,z);