
Федеральное агентство по образованию

Санкт-Петербургский государственный
электротехнический университет «ЛЭТИ»

Кафедра «Вычислительная техника»
В работе есть ошибка! Один из путей в графе упущен (стр 7)! Его надо добавить, но это повлечет перерасчет всей работы.
контрольная работа
ПО ДИСЦИПЛИНЕ
«Микропрограммное управление и теория автоматов»
Вариант № 13
Выполнил:
Группа:
Санкт-Петербург
2013
Оглавление
2.Абстрактный синтез автомата 4
3.Структурный синтез автомата 12
-
Задание
У0

X1
У2
У3
У1
Х2
У3
Х1
У2
У1
У3
Х3
1
0
0
1
1
0
0
1
У0






















Таблица влияний микроопераций на значение логических условий
|
|
Х1 |
Х2 |
Х3 |
|
У0 |
|
0 |
|
|
У1 |
|
¬ |
Z |
|
У2 |
|
|
0 |
|
У3 |
¬ |
|
|
|
U0 |
0 |
0 |
0 |
RS-триггер
3И-НЕ, Кр=4
ПЗУ: n=6, m=8
ПЛМ: n=6, t=8, m=4
-
Абстрактный синтез автомата
-
Граф автомата Мура.
-
Сопоставим вершинам ГСА символы состояний Sx.
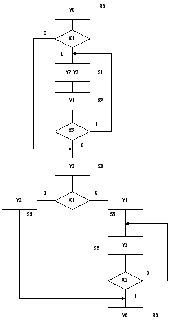
Дальше построим граф для исходной ГСА:

-
Проверка автомата Мура.
Необходимым, но не достаточным условием правильности построения графа автомата по ГСА микропрограммы является существование переходов из каждого состояния по каждому из 2n наборов значений логических условий.
Таблица переходов и выходов
|
Y0 Y1 Y2 Y3 |
Si |
X1 X2 X3 |
|||||||
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
||
|
1 0 0 0 |
S0 |
S3 |
S3 |
S3 |
S3 |
S1 |
S1 |
S1 |
S1 |
|
0 1 1 0 |
S1 |
S2 |
S2 |
S2 |
S2 |
S2 |
S2 |
S2 |
S2 |
|
1 0 0 0 |
S2 |
S3 |
S3 |
S1 |
S1 |
S3 |
S3 |
S1 |
S1 |
|
0 0 0 1 |
S3 |
S5 |
S5 |
S5 |
S5 |
S4 |
S4 |
S4 |
S4 |
|
0 0 1 0 |
S4 |
S0 |
S0 |
S0 |
S0 |
S0 |
S0 |
S0 |
S0 |
|
1 0 0 0 |
S5 |
S6 |
S6 |
S6 |
S6 |
S6 |
S6 |
S6 |
S6 |
|
0 0 0 1 |
S6 |
S6 |
S0 |
S6 |
S0 |
S6 |
S0 |
S6 |
S0 |
-
Переход к автомату Мили
В результате переноса для каждого состояния выходных сигналов, которыми отмечены эти состояния, на входящие дуги получается граф автомата Мили. Эквивалентных состояний S0 в данном автомате нет.
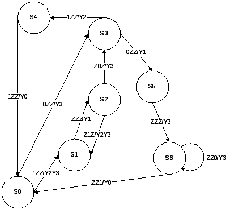
|
Y0 Y1 Y2 Y3 |
Si |
X1 X2 X3 |
|||||||
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
||
|
1 0 0 0 |
S0 |
S3/Y3 |
S3/Y3 |
S3/Y3 |
S3/Y3 |
S1/Y2Y3 |
S1/Y2Y3 |
S1/Y2Y3 |
S1/Y2Y3 |
|
0 1 1 0 |
S1 |
S2/Y1 |
S2/Y1 |
S2/Y1 |
S2/Y1 |
S2/Y1 |
S2/Y1 |
S2/Y1 |
S2/Y1 |
|
1 0 0 0 |
S2 |
S3/Y3 |
S3/Y3 |
S1/Y2Y3 |
S1/Y2Y3 |
S3/Y3 |
S3/Y3 |
S1/Y2Y3 |
S1/Y2Y3 |
|
0 0 0 1 |
S3 |
S5/Y1 |
S5/Y1 |
S5/Y1 |
S5/Y1 |
S4/Y2 |
S4/Y2 |
S4/Y2 |
S4/Y2 |
|
0 0 1 0 |
S4 |
S0/Y0 |
S0/Y0 |
S0/Y0 |
S0/Y0 |
S0/Y0 |
S0/Y0 |
S0/Y0 |
S0/Y0 |
|
1 0 0 0 |
S5 |
S6/Y3 |
S6/Y3 |
S6/Y3 |
S6/Y3 |
S6/Y3 |
S6/Y3 |
S6/Y3 |
S6/Y3 |
|
0 0 0 1 |
S6 |
S6/Y3 |
S0/Y0 |
S6/Y3 |
S0/Y0 |
S6/Y3 |
S0/Y0 |
S6/Y3 |
S0/Y0 |
-
Получение частичного автомата Мили
Значения логических условий:
|
Y0: |
X1=X1 |
X2=0 |
X3=X3 |
|
Y1: |
X1=X1 |
X2=¬X2 |
X3=Z |
|
Y2: |
X1=X1 |
X2=X2 |
X3=0 |
|
Y3: |
X1=¬X1 |
X2=X2 |
X3=X3 |
|
Y2Y3: |
X1=¬X1 |
X2=X2 |
X3=0 |
|
U0: |
X1=0 |
X2=0 |
X3=0 |
Для определения наборов значений логических условий надо последовательно и многократно просматривать все пути в графе автомата до тех пор, пока для каждого состояния Si его множество входных наборов Ui не будет устойчивым, т.е. пока не перестанут появляться новые наборы в множествах Ui.
Входной набор перед началом работы U0 = 000.
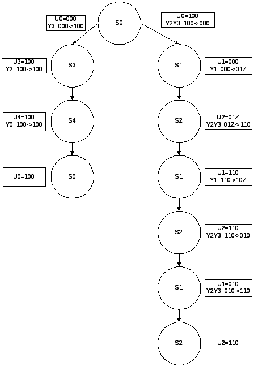
U0={000, 100}
U1={000, 110, 010}
U2={010, 011, 110}
U3={100}
U4={100}
Получаем таблицу частичного автомата Мили
|
Y0 Y1 Y2 Y3 |
Si |
X1 X2 X3 |
|||||||
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
||
|
1 0 0 0 |
S0 |
S3/Y3 |
- |
- |
- |
S1/Y2Y3 |
- |
- |
- |
|
0 1 1 0 |
S1 |
S2/Y1 |
- |
S2/Y1 |
- |
- |
- |
S2/Y1 |
- |
|
1 0 0 0 |
S2 |
- |
- |
S1/Y2Y3 |
S1/Y2Y3 |
- |
- |
S1/Y2Y3 |
- |
|
0 0 0 1 |
S3 |
- |
- |
- |
- |
S4/Y2 |
- |
- |
- |
|
0 0 1 0 |
S4 |
- |
- |
- |
- |
S0/Y0 |
- |
- |
- |
|
1 0 0 0 |
S5 |
- |
- |
- |
- |
- |
- |
- |
- |
|
0 0 0 1 |
S6 |
- |
- |
- |
- |
- |
- |
- |
- |
-
Минимизация автомата Мили
Полученная таблица переходов и выходов частичного автомата определяет структурный автомат с абстрактными состояниями. Произвольно декодируя входной и выходной алфавиты, можно получить таблицу переходов и выходов абстрактного автомата.
|
|
|
Si |
Pi |
|||||||
|
P0 |
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
P7 |
|
|
S0 |
S3/W3 |
- |
- |
- |
S1/W4 |
- |
- |
- |
|
S1 |
S2/W1 |
- |
S2/W1 |
- |
- |
- |
S2/W1 |
- |
|
S2 |
- |
- |
S1/W4 |
S1/W4 |
- |
- |
S1/W4 |
- |
|
S3 |
- |
- |
- |
- |
S4/W2 |
- |
- |
- |
|
S4 |
- |
- |
- |
- |
S0/W0 |
- |
- |
- |
|
S5 |
- |
- |
- |
- |
- |
- |
- |
- |
|
S6 |
- |
- |
- |
- |
- |
- |
- |
- |
|
S1 |
Х |
|
|
|
|
|
|
S2 |
- |
Х |
|
|
|
|
|
S3 |
Х |
- |
- |
|
|
|
|
S4 |
Х |
- |
- |
Х |
|
|
|
S5 |
Х |
Х |
Х |
Х |
Х |
|
|
S6 |
Х |
Х |
Х |
Х |
Х |
Х |
|
|
S0 |
S1 |
S2 |
S3 |
S4 |
S5 |
Совместимые состояния:
S0 – S2
S1 – S3
S1 - S4
S2 – S3
S2 – S4
S0-S2->S0
S1-S3->S1
S2-S4->S2
|
Si |
Pi |
|||||||
|
P0 |
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
P7 |
|
|
S0 |
S3/W3 |
- |
S1/W4 |
S1/W4 |
S1/W4 |
- |
S1/W4 |
- |
|
S1 |
S2/W1 |
- |
S2/W1 |
- |
S2/W2 |
- |
S2/W1 |
- |
|
S2 |
- |
- |
|
|
S0/W0 |
- |
|
- |
|
Si |
X1 X2 X3 |
|||||||
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
|
S0 |
S3/0001 |
- |
S1/0011 |
S1/0011 |
S1/0011 |
- |
S1/0011 |
- |
|
S1 |
S2/0100 |
- |
S2/0100 |
- |
S2/0010 |
- |
S2/0100 |
- |
|
S2 |
- |
- |
- |
- |
S0/1000 |
- |
- |
- |
-
Проверка минимального автомата Мили
|
X1 X2 X3 |
Y0 Y1 Y2 Y3 |
|
000 |
1000 |
|
100 |
0001 |
|
100 |
0010 |
|
100 |
1000 |
|
010 |
0011 |
|
001 |
0100 |
|
101 |
0001 |
|
100 |
0010 |
|
S(t) |
X1 X2 X3 |
S(t+1) |
Y0 Y1 Y2 Y3 |
|
S0 |
000 |
S0 |
1000 |
|
S0 |
100 |
S3 |
0001 |
|
S3 |
100 |
S2 |
0010 |
|
S0 |
100 |
S1 |
1000 |
|
S1 |
010 |
S2 |
0011 |
|
S2 |
001 |
S3 |
0100 |
|
S3 |
101 |
S2 |
0001 |
|
S2 |
100 |
S0 |
0010 |
