2. Управляемые преобразователи напряжения и тока

2.1. Генераторы постоянного тока независимого возбуждения

Генераторы постоянного тока используются в качестве регулируемых источников напряжения в различных системах автоматики. Наиболее часто они используются в системах регулируемого электропривода постоянного тока. Генератор - это электромеханический преобразователь энергии. Он преобразует механическую энергию, поступающую на его вал от приводного двигателя, в электрическую энергию постоянного тока. Конструктивные особенности генераторов подробно рассматриваются в /3/.

Достоинства преобразовательного агрегата из приводного двигателя переменного тока и генератора постоянного тока:

- линейность преобразования управляющего сигнала в выходную ЭДС в широком диапазоне его изменения;

- хорошая перегрузочная способность;

- отсутствие искажений напряжения питающей сети переменного тока от работы генератора и возможность работы с высоким коэффициентом мощности.

Недостатки агрегата:

- существенная инерционность при отработке сигнала управления по каналу возбуждения генератора;

- плохие массогабаритные показатели и значительные затраты на его установку;

- вибрация и шум при работе агрегата;

- относительно невысокий результирующий КПД из-за многократного преобразования энергии.

У генераторов общего назначения перегрузочная способность по току равна 2 при длительности перегрузки до 3 с и равна 1,5 при продолжительности перегрузки до 60 с.

Регулировать выходную ЭДС генератора можно двумя способами: изменением напряжения на обмотке возбуждения и изменением скорости вращения вала генератора. Регулирование изменением скорости вращения очень редко используется в схемах автоматики и здесь рассматриваться не будет.

С

а)

б)

хема включения генератора при регулировании его выходного напряжения изменением напряжения возбуждения приведена на рис. 2.1, а.

Р ис. 2.1. Генератор постоянного тока независимого возбуждения:

а - принципиальная схема; б - структурная схема

На рис. 2.1 приняты следующие обозначения: G - обмотка якоря генератора; ОВ - независимая обмотка возбуждения; Н - цепь нагрузки генератора; u_в - напряжение возбуждения; i_в - ток возбуждения; _г - угловая скорость вращения вала генератора; Ф - поток возбуждения от намагничивающей силы на один полюс генератора; u_г - напряжение на выходе генератора; i - ток якоря генератора; u_в(p) - изображение по Лапласу напряжения возбуждения; е_г(p) - изображение по Лапласу выходной ЭДС генератора; W_г(p) - передаточная функция генератора по Лапласу; 1 и 2 - зажимы для подключения источника напряжения возбуждения; 3 и 4 - зажимы для подключения цепи нагрузки генератора.

Рассмотрим характеристики генератора независимого возбуждения при общепринятых в инженерных расчетах допущениях, полагая, что петля гистерезиса характеристики намагничивания генератора достаточно узка и ее не учитываем; насыщением магнитных цепей генератора и реакцией якоря пренебрегаем; скорость вала генератора считаем постоянной; влиянием вихревых токов, увеличивающих инерционность цепи возбуждения, пренебрегаем. Также пренебрегаем влиянием индуктивности якорной цепи генератора на его выходное напряжение. При таких допущениях процессы в генераторе описываются системой линейных уравнений:

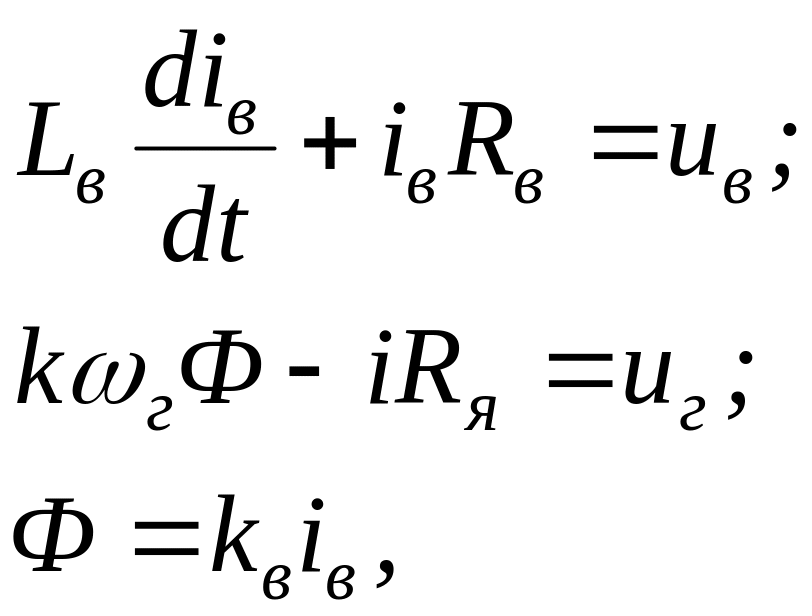(2.1)

где L_в - индуктивность цепи возбуждения; R_в - активное сопротивление цепи возбуждения; k = pN/(2a) - конструктивная постоянная машины; p - число пар полюсов; а - число пар параллельных ветвей якорной обмотки; N - число активных проводников якорной обмотки; R_я - активное сопротивление якорной цепи; k_в - коэффициент, связывающий поток возбуждения на один полюс с током цепи возбуждения, Вб/А.

Индуктивность цепи возбуждения находится по формуле

,

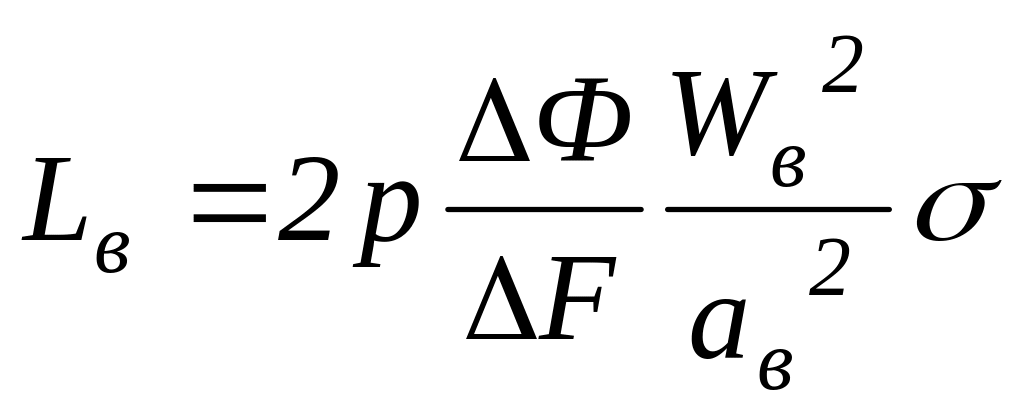где Ф и F - приращение магнитного потока и соответствующее ему приращение намагничивающей силы на один полюс, которые можно определить по линейному рабочему участку кривой намагничивания генератора; W_в - число витков обмотки возбуждения на один полюс; а_в - число параллельных ветвей обмотки возбуждения;  - коэффициент, учитывающий рассеяние магнитного потока полюсов.

По кривой намагничивания также определяется коэффициент

В установившемся режиме di_в /dt = 0 и соответственно для статического режима уравнения (2.1) преобразуются к виду:

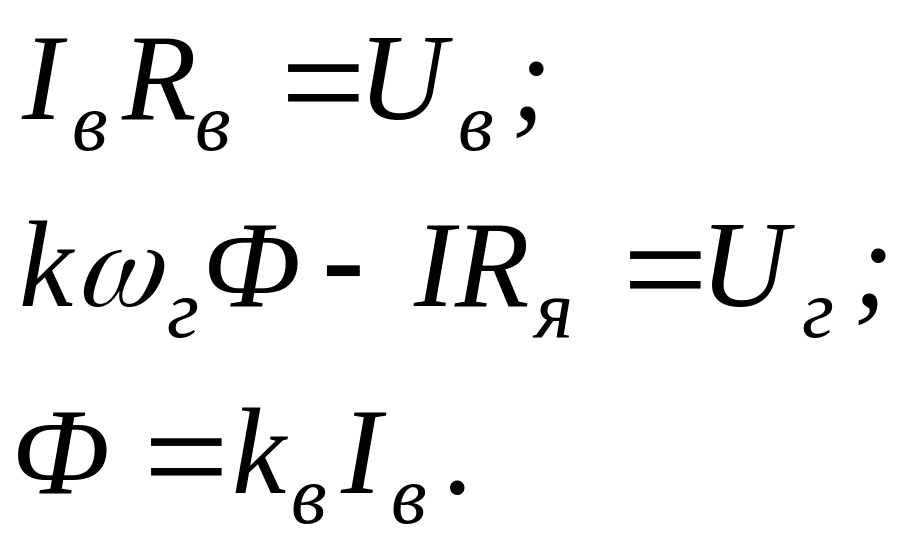(2.2)

Прописными буквами в данных уравнениях обозначены токи и напряжения в установившемся режиме.

Из (2.2) может быть найдено выражение для расчета статического значения выходной координаты генератора

(2.3)

где k_г = kk_в_г /R_в - коэффициент усиления генератора.

Принимая в (2.3) за аргумент напряжение возбуждения U_в, а за параметр  возмущающее воздействие в виде тока якоря I, получим семейство характеристик управления, которое приведено на рис. 2.2, а. Если за аргумент принять ток I, а за параметр  напряжение U_в, то получим семейство внешних характеристик, приведенное на рис. 2.2, б.

Рис. 2.2. Статические характеристики генератора:

а - управления; б - внешние

Если в качестве выходной величины принято напряжение генератора u_г, как следует из рис. 2.2, а, то характеристики управления будут неоднозначны. Неоднозначность обусловлена наличием падения напряжения на сопротивлении якорной цепи генератора. Неоднозначность характеристик управления будет исключена, если в качестве выходной координаты элемента рассматривать ЭДС генератора, как показано на рис. 2.2, б. При таком представлении генератора сопротивление его якорной цепи можно рассматривать в составе цепи внешней нагрузки генератора. При таком представлении генератора характеристика управления единственная, и ее формула имеет вид

,

г де Е_г- установившееся значение ЭДС генератора. Соответственно внешние характеристики будут абсолютно жесткими. Характеристика управления приведена на рис. 2.3, а, а внешние характеристики  на рис. 2.3, б.

Рис. 2.3. Статические характеристики генератора как источника ЭДС:

а - управления; б - внешние

Введя для обозначения операции дифференцирования символ p, то есть , и полагая, что на холостом ходу i = 0, а u_г = е_г, систему (2.1) можно записать в виде

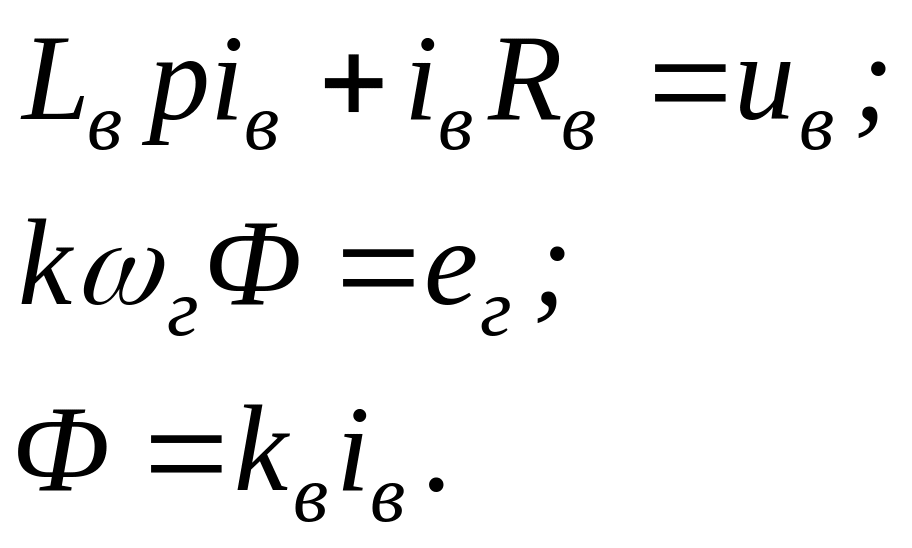
Из последней системы после несложных преобразований может быть получена передаточная функция генератора по входной величине u_в в операторном виде:

,

где T_в = L_в/R_в - электромагнитная постоянная времени цепи возбуждения.

Система (2.1) имеет неизменные во времени коэффициенты. Поэтому при нулевых начальных условиях передаточная функция генератора по Лапласу с точностью до обозначений совпадает с операторной передаточной функцией и равна

. (2.4)

Как следует из передаточной функции (2.4), процессы в генераторе по управлению соответствуют апериодическому звену первого порядка, которое имеет переходную характеристику вида

Переходная характеристика приведена на рис. 2.4, б.

На рис. 2.4, а приведены частотные характеристики генератора: кривая L() - амплитудно-частотная характеристика, кривая () – фазово-частотная характеристика.

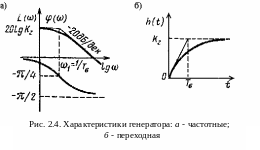
Как следует из графика переходной характеристики, быстродействие генератора при отработке управляющего воздействия U_в определяется величиной постоянной времени цепи возбуждения T_в. Увеличение активного сопротивления цепи возбуждения R_в увеличивает быстродействие, но при этом возрастают активные потери электрической энергии на этом сопротивлении.

Снижение быстродействия генератора из-за эффекта вихревых токов может быть учтено путем увеличения электромагнитной постоянной времени цепи возбуждения T_в на 10 – 15 % . Представление различных генераторов постоянного тока как элементов систем автоматики более подробно рассмотрено в /1/.