
- •Элементы систем автоматики
- •Введение
- •1. Элементы систем автоматики и их характеристики
- •1.1. Понятие об элементах и их классификация
- •Вопросы для самопроверки
- •1.2. Основные координаты, основные характеристики и математическое описание элементов
- •Вопросы для самопроверки
- •2. Управляемые преобразователи напряжения и тока
- •2.1. Генераторы постоянного тока независимого возбуждения
- •Вопросы для самопроверки
- •2.2. Электромашинные усилители
- •Вопросы для самопроверки
- •2.3. Магнитные усилители с выходом на постоянном токе
- •Вопросы для самопроверки
- •2.4. Управляемые выпрямители
- •Вопросы для самопроверки
- •2.5. Широтно-импульсные преобразователи
- •Вопросы для самопроверки
- •2.6. Трехфазные преобразователи частоты с автономными инверторами
- •Вопросы для самопроверки
- •2.7. Преобразователи частоты с непосредственной связью с сетью
- •Вопросы для самопроверки
- •3. Электрические двигатели
- •3.1. Электрические двигатели постоянного тока независимого возбуждения
- •Вопросы для самопроверки
- •3.2. Асинхронные электрические двигатели
- •Вопросы для самопроверки
Вопросы для самопроверки
Какое преобразование энергии осуществляется двигателем постоянного тока в двигательном и генераторном режиме его работы?
В чем основные достоинства двигателей постоянного тока независимого возбуждения?
Что является входными координатами двигателя постоянного тока независимого возбуждения?
Что является возмущающим воздействием двигателя постоянного тока независимого возбуждения?
Что является выходной координатой двигателя постоянного тока независимого возбуждения?
Какая входная координата изменяется, а какая остается неизменной при регулировании скорости двигателя в первой зоне?
Какая входная координата изменяется, а какая остается неизменной при регулировании скорости двигателя во второй зоне?
Перечислите основные упрощающие допущения, при которых процессы в двигателе постоянного тока независимого возбуждения будут описываться системой линейных уравнений.
Приведите формулы для расчета характеристик управления и внешних (нагрузочных) характеристик двигателя постоянного тока независимого возбуждения.
Приведите формулы для расчета электромагнитных постоянных времени якорной цепи и цепи возбуждения двигателя постоянного тока независимого возбуждения.
Приведите формулу передаточной функции, описывающей регулирование скорости двигателя постоянного тока независимого возбуждения на холостом ходу путем изменения напряжения якоря.
Приведите формулу для расчета электромеханической постоянной времени якорной цепи и цепи возбуждения двигателя постоянного тока независимого возбуждения.
Каким динамическим звеном может быть представлен двигатель постоянного тока независимого возбуждения при регулировании скорости на холостом ходу изменением напряжения якоря, когда
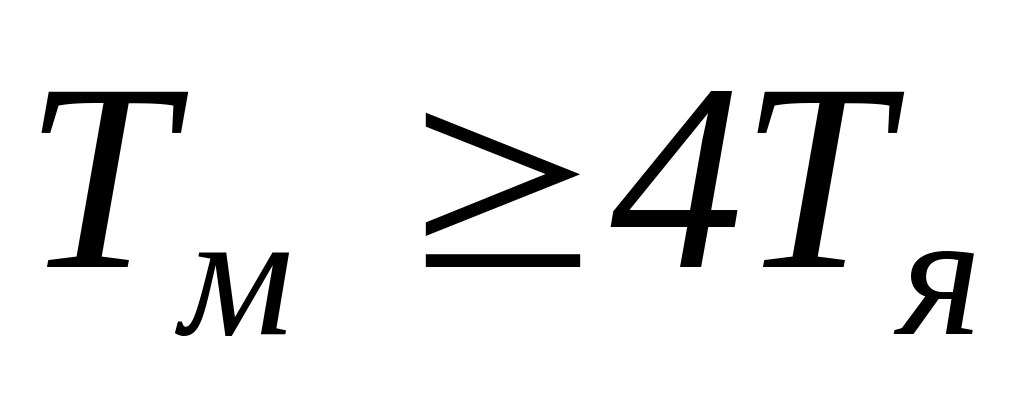 ?
?Каким динамическим звеном может быть представлен двигатель постоянного тока независимого возбуждения при регулировании скорости на холостом ходу изменением напряжения якоря, когда
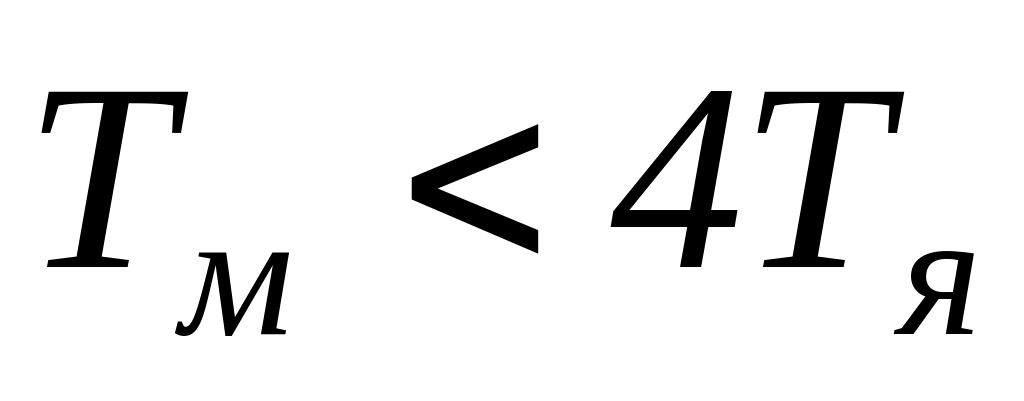 ?
?Какие основные недостатки характерны для двигателей постоянного тока?
3.2. Асинхронные электрические двигатели
Асинхронные электродвигатели более дешевы и надежны, чем электродвигатели постоянного тока и имеют лучшие массогабаритные показатели при той же мощности на валу.
Асинхронные двигатели с короткозамкнутым ротором не имеют узлов со скользящими контактами, что исключает искрообразование при нормальной работе и делает перспективным использование таких двигателей во взрывоопасных, пожароопасных и других агрессивных средах. Однако, по сравнению с двигателями постоянного тока независимого возбуждения, асинхронные двигатели, и особенно двигатели с короткозамкнутым ротором, имеют худшие регулировочные свойства, требуют более сложно реализуемых способов регулирования скорости, и их характеристики нелинейны.
Асинхронные двигатели бывают однофазными, двухфазными и трехфазными. Конструкция таких двигателей подробно рассмотрена в /2, 3/.
В системах автоматики в основном применяются двухфазные и трехфазные асинхронные двигатели.
Двухфазные электродвигатели. Их применяют обычно в маломощных исполнительных механизмах и следящих системах. В основном выпускают двухфазные асинхронные двигатели двух типов: с полым немагнитным ротором (обычно из алюминия) и с ферромагнитным ротором, имеющим короткозамкнутую обмотку в виде беличьей клетки. Двигатели с полым ротором обладают большим быстродействием.
На статоре двигателя уложены две обмотки, сдвинутые в пространстве на 90 электрических градусов. Одна из них - обмотка возбуждения (OB) - включается в сеть переменного тока на напряжение возбуждения Uв, на другую - обмотку управления (ОУ) - подается сигнал управления в виде переменного напряжения управления Uу.
Сдвиг по фазе между напряжениями Uв и Uу, необходимый для получения вращающегося поля, создают включением в цепь обмоток конденсаторов.
Регулирование скорости вращения исполнительных асинхронных двигателей осуществляют путем изменения напряжения Uу при постоянстве его фазы (амплитудное управление) или изменения фазы постоянного по величине напряжения Uу (фазовое управление). Часто применяют амплитудно-фазовое управление двигателем при одновременном изменении величины и фазы напряжения управления относительно напряжения возбуждения. Направление вращения ротора исполнительного двигателя зависит от того, какое из напряжений (Uв или Uу) является опережающим по фазе.
Одно из главных требований, предъявляемых к исполнительному двигателю, заключается в том, что при снятии сигнала ротор должен остановиться без применения каких-либо тормозящих устройств, то есть должен отсутствовать самоход. Для того чтобы это требование выполнялось, необходимо повысить активное сопротивление ротора до такой величины, при которой критическое скольжение по отношению к магнитному полю прямой последовательности в воздушном зазоре двигателя было не меньше единицы.
П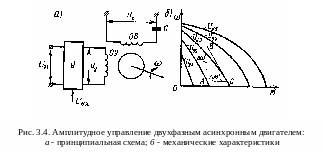 ринципиальная
схема включения двухфазного асинхронного
двигателя при амплитудном управлении
показана на рис. 3.4, а.
Оси обмоток управления ОУ
и возбуждения ОВ
смещены на 90 электрических градусов
и питаются от источников переменного
тока одинаковой частоты. Необходимый
для создания вращающего поля фазовый
сдвиг между напряжениями на обмотках,
близкий к 90 электрическим градусам,
может обеспечивается с помощью
конденсатора С
(или любыми другими способами). Напряжение
управления двигателем Uу
подается на обмотку ОУ
от усилителя У.
В качестве такого усилителя обычно
используется полупроводниковый
усилитель с выходом на переменном токе,
амплитудная и фазовая характеристики
управления которого приведены на рис.
3.5. На этом рисунке использованы
обозначения: Uвх
- напряжение управления на входе
управления усилителя; Uвхм
- максимальное напряжение управления;
- сдвиг между переменным напряжением
uу
и переменным
напряжением uв.
При положительных значениях Uвх
двигатель вращается в условном
направлении "вперед", а при
отрицательных Uвх
- "назад".
ринципиальная
схема включения двухфазного асинхронного
двигателя при амплитудном управлении
показана на рис. 3.4, а.
Оси обмоток управления ОУ
и возбуждения ОВ
смещены на 90 электрических градусов
и питаются от источников переменного
тока одинаковой частоты. Необходимый
для создания вращающего поля фазовый
сдвиг между напряжениями на обмотках,
близкий к 90 электрическим градусам,
может обеспечивается с помощью
конденсатора С
(или любыми другими способами). Напряжение
управления двигателем Uу
подается на обмотку ОУ
от усилителя У.
В качестве такого усилителя обычно
используется полупроводниковый
усилитель с выходом на переменном токе,
амплитудная и фазовая характеристики
управления которого приведены на рис.
3.5. На этом рисунке использованы
обозначения: Uвх
- напряжение управления на входе
управления усилителя; Uвхм
- максимальное напряжение управления;
- сдвиг между переменным напряжением
uу
и переменным
напряжением uв.
При положительных значениях Uвх
двигатель вращается в условном
направлении "вперед", а при
отрицательных Uвх
- "назад".
М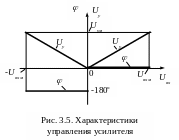 еханические
характеристики двухфазного двигателя
(рис. 3.4, б)
нелинейны и, как правило, определяются
экспериментально при управлении по
схеме на рис. 3.4, а
от усилителя с большой мощностью и
малым внутренним сопротивлением.
Величина емкости С указывается в
технических данных двигателя. Обычно
ее выбирают из условия получения
кругового поля при неподвижном двигателе.
Каждая из характеристик
= f(М)
соответствует определенному значению
амплитуды Uу
напряжения управления (Uу5
> Uу4
> > Uу3
> Uу2>Uу1
).
еханические
характеристики двухфазного двигателя
(рис. 3.4, б)
нелинейны и, как правило, определяются
экспериментально при управлении по
схеме на рис. 3.4, а
от усилителя с большой мощностью и
малым внутренним сопротивлением.
Величина емкости С указывается в
технических данных двигателя. Обычно
ее выбирают из условия получения
кругового поля при неподвижном двигателе.
Каждая из характеристик
= f(М)
соответствует определенному значению
амплитуды Uу
напряжения управления (Uу5
> Uу4
> > Uу3
> Uу2>Uу1
).
Аппроксимируя механические характеристики двигателя в точке или области рабочего режима отрезками прямых (рис. 3.4, б), можно записать линеаризованное уравнение механической характеристики в приращениях переменных при амплитудном управлении двигателем. Построим треугольник ABC, как показано на рис. 3.4 б. Гипотенуза треугольника должна быть касательной к механической характеристике в точке C. Учитывая, что приращение напряжения управления U'у = Uу3 - Uу2, получим
Δ = (Δ'/ΔU'у)ΔUу - (Δ'/ΔM')ΔM = kдΔUу - kдмΔM, (3.7)
где kд = (Δ'/ΔU'у) и kдм = (Δ'/ΔM')- коэффициенты передачи двигателя соответственно по управляющему воздействию и по моменту.
Уравнение движения в приращениях при статическом моменте Mс на валу двигателя, не зависящим от скорости, будет иметь вид
ΔM - ΔMс = JpΔ, (3.8)
где p - оператор дифференцирования d/(dt).
Поскольку постоянные времени всех элементов цепи управления и электромагнитная постоянная времени двигателя малы, по сравнению с электромеханической постоянной времени, ими можно пренебречь. Тогда дифференциальное уравнение двигателя находим из уравнений (3.7) и (3.8):
![]() ,
(3.9)
,
(3.9)
где Тм = Jkдм - электромеханическая постоянная времени асинхронного двигателя, прямо пропорциональная моменту инерции ротора и обратно пропорциональная жесткости механических характеристик.
Таким образом, двухфазный двигатель в динамике можно упрощенно рассматривать как апериодическое звено. Передаточная функция двигателя по управляющему воздействию Uу(p)
![]() ,
(3.11)
,
(3.11)
а по возмущающему воздействию Mс(p)
![]() .
(3.12)
.
(3.12)
Трехфазные электродвигатели. В отличие от двухфазных, трехфазные асинхронные двигатели выпускаются на широкий диапазон мощностей, в том числе и мощности в тысячи киловатт. Трехфазные асинхронные двигатели бывают с фазным и короткозамкнутым ротором. Наиболее часто они управляются тремя способами: изменением добавочных сопротивлений в цепи ротора (двигатели с фазным ротором), изменением напряжения, подводимого к статору, и совместным изменением частоты и напряжения питания статора. Последний способ применяют только для короткозамкнутых двигателей, хотя данный способ регулирования скорости принципиально пригоден и для асинхронных двигателей с фазным ротором, но нецелесообразен по технико-экономическим соображениям.
Асинхронный двигатель в динамике описывается системой трансцендентных дифференциальных уравнений, решение которых возможно лишь при использовании вычислительных машин. Однако в ряде частных случаев можно рассматривать переходные процессы в приводах с асинхронными двигателями, исходя из упрощенных дифференциальных уравнений, которые приводят к виду, удобному для аналитического исследования.
Управление по первому способу может осуществляться либо ступенчато (при контакторном управлении), либо плавно (в системах с тиристорными коммутаторами). Механические характеристики двигателя в этих случаях описываются известным упрощенным уравнением
M = 2Mкр /(s / sкр + sкр / s), ( 3.13)
г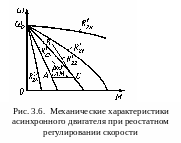 де
Мкр
- критический момент; s
= (о
- )
/ о
скольжение;
де
Мкр
- критический момент; s
= (о
- )
/ о
скольжение;
![]() -
критическое скольжение. Здесь R'2
- приведенное
полное активное сопротивление ротора
(для естественной характеристики оно
будет R'2е
); xкз
- индуктивное сопротивление короткого
замыкания двигателя. Значение критического
момента может быть рассчитано по
справочным данным двигателя по известной
из теории электропривода методике.
-
критическое скольжение. Здесь R'2
- приведенное
полное активное сопротивление ротора
(для естественной характеристики оно
будет R'2е
); xкз
- индуктивное сопротивление короткого
замыкания двигателя. Значение критического
момента может быть рассчитано по
справочным данным двигателя по известной
из теории электропривода методике.
Рассматривая R'2 как параметр управления, можно по уравнению (3.13) построить семейство механических характеристик (рис. 3.6), где R'24 > R'23 > R'22 > R'21 >R'2е. Линеаризуем характеристики подобно тому, как было сделано для двухфазного двигателя, и учтем, что ΔR'2 = = R'23 - R'22. Тогда уравнение механической характеристики в приращениях
Δ = - kдΔR'2 - kдмΔM, (3.14)
где kд = Δ' / R'2 и kдм = Δ' / ΔM - коэффициенты передачи двигателя. При наличии в роторе добавочных сопротивлений можно пренебречь влиянием электромагнитных переходных процессов в обмотках двигателя. В этом случае из (3.8) и (3.14) получим дифференциальное уравнение, аналогичное (3.9), если в последнем вместо Uу принять ΔR'2.
Когда управление двигателем с фазным ротором производится по второму способу - изменением напряжения статора - двигатель при этом подключается к сети через дроссельный или тиристорный регулятор.
Д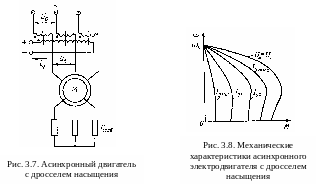 россельный
регулятор переменного напряжения - это
трехфазный магнитный усилитель с
выходом на переменном токе, через
рабочие обмотки которого подается
напряжение на фазы статора двигателя.
Регулирование действующего значения
напряжения на статоре производится
изменением тока подмагничивания Iу
обмотки
управления. Простейшая схема такого
усилителя, работающего на двигатель,
приведена на рис. 3.7, а механические
характеристики двигателя при регулировании
скорости изменением напряжения на
статоре - на рис. 3.8.
россельный
регулятор переменного напряжения - это
трехфазный магнитный усилитель с
выходом на переменном токе, через
рабочие обмотки которого подается
напряжение на фазы статора двигателя.
Регулирование действующего значения
напряжения на статоре производится
изменением тока подмагничивания Iу
обмотки
управления. Простейшая схема такого
усилителя, работающего на двигатель,
приведена на рис. 3.7, а механические
характеристики двигателя при регулировании
скорости изменением напряжения на
статоре - на рис. 3.8.
Трехфазный тиристорный регулятор переменного напряжения в каждой фазе входного напряжения питающей сети содержит по два тиристора, включенных встречно-параллельно, через которые подается напряжение на статор двигателя (рис. 3.9). Регулирование действующего значения напряжения на статоре двигателя производится изменением угла отпирания импульсов управления тиристорами, которые формируются системой импульсно-фазового управления, во многом похожей на систему импульсно-фазового управления тиристорами обычного выпрямителя. Схемы тиристорных регуляторов напряжения, их работа и характеристики рассмотрены в /1, 5/ . Механические характеристики асинхронного двигателя при питании его от тиристорного регулятора напряжения аналогичны семейству характеристик рис. 3.8 , если в последних в качестве параметра брать угол управления . Характеристики с большим критическим моментом соответствуют меньшим значениям угла .. На рис. 3.7, 3.8 и 3.9 обозначены: iу - ток обмотки управления; Uд - напряжение на статоре двигателя; Uс - напряжение питающей сети.
Линеаризованные уравнения механических характеристик будут подобны уравнению (3.14). Можно также пренебречь электромагнитной инерцией обмоток двигателя, поэтому дифференциальное уравнение двигателя будет аналогично (3.9), если в последнем заменить ΔUу соответственно на ΔIу или на Δ. Коэффициент передачи при этом будет kд = Δ' / ΔI'у или kд = Δ' / Δ'. Линеаризация механических характеристик при таких способах регулирования напряжения на статоре производится аналогично линеаризации характеристик рис. 3.4, б, но с заменой приращения ΔU'у на ΔI'у или на Δ'. При этом Δ' = -(3 - 2), где 3 - угол отпирания на характеристике при большем напряжении на статоре, а 2 - угол отпирания на характеристике при меньшем напряжении на статоре. Следовательно, при принятом выше допущении и линеаризации трехфазный асинхронный двигатель, управляемый изменением напряжения на статоре любым из двух рассмотренных способов, с точки зрения динамики, представляет собой апериодическое звено и его передаточные функции аналогичны передаточным функциям двухфазного двигателя (3.11) и (3.12).
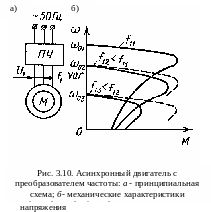 Для
осуществления третьего (частотного)
способа регулирования двигатель
подключают к электромашинному или
тиристорному преобразователю частоты
ПЧ
(рис. 3.10, а).
Если в этом случае одновременно с
частотой f1
регулировать
напряжение U1
таким
образом, чтобы U1
/f1
= const,
то механические характеристики двигателя
будут иметь вид сплошных кривых,
показанных на рис. 3.10, б.
Если система управления преобразователем
частоты предусматривает компенсацию
падения напряжения в активном
сопротивлении R1
статора
двигателя, то есть поддерживается
постоянство отношения (U1
-I1R1)
/ f1,
то механические характеристики двигателя
принимают вид кривых, выполненных на
рис. 3.10, б
штриховыми линиями. В последнем случае
сохраняется постоянной перегрузочная
способность двигателя. Методика
расчета механических характеристик
при f1
= var
дана в литературе по теории электропривода.
Для
осуществления третьего (частотного)
способа регулирования двигатель
подключают к электромашинному или
тиристорному преобразователю частоты
ПЧ
(рис. 3.10, а).
Если в этом случае одновременно с
частотой f1
регулировать
напряжение U1
таким
образом, чтобы U1
/f1
= const,
то механические характеристики двигателя
будут иметь вид сплошных кривых,
показанных на рис. 3.10, б.
Если система управления преобразователем
частоты предусматривает компенсацию
падения напряжения в активном
сопротивлении R1
статора
двигателя, то есть поддерживается
постоянство отношения (U1
-I1R1)
/ f1,
то механические характеристики двигателя
принимают вид кривых, выполненных на
рис. 3.10, б
штриховыми линиями. В последнем случае
сохраняется постоянной перегрузочная
способность двигателя. Методика
расчета механических характеристик
при f1
= var
дана в литературе по теории электропривода.
При частотном управлении параметром, характеризующим управляющее воздействие, является частота питающего напряжения f1, т. е. синхронная скорость о = 2f1 / p, где р - число пар полюсов обмотки статора двигателя.
В
упрощенном виде с учетом электромагнитных
переходных процессов в двигателе
при частотном управлении его динамика
описывается следующими дифференциальными
уравнениями: уравнением равновесия
моментов (3.8) и зависимостью момента
двигателя М
от скольжения s
(при работе двигателя на спрямленном
участке механической характеристики
от М
= 0 до
![]() ,
где Mн
- номинальный момент двигателя)
,
где Mн
- номинальный момент двигателя)
(Tэфp+1)M = Mфs, (3.15)
где - Tэф =1/(оsкр) - фиктивная электромагнитная постоянная времени двигателя; Mф = 2Mкр / sкр - фиктивный электромагнитный момент при = 0; Mкр и sкр - критические момент и скольжение для данной характеристики. Учитывая, что s = (Δо -Δ) /о, и переходя в (3.15) к приращениям переменных в окрестности точки с начальными значениями скорости и момента, получим (полагая, что Δs = (Δo - Δo) /о) следующие уравнения:
(Tэфp+1)ΔM = (1 / kдм)(Δо - Δ), (3.16)
где kдм = Δ / ΔM = o / Mф - коэффициент передачи двигателя по моменту;
ΔM - ΔMс = JpΔ = ΔTмp / kдм; (3.17)
Δо = 2/p Δf1 = kд Δf1, (3.18)
где Tм = Jkдм - электромеханическая постоянная времени двигателя; kд = Δo/Δf1 = 2/p - коэффициент передачи двигателя (p - число пар полюсов двигателя).
У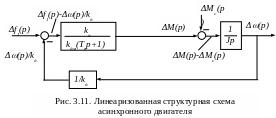 равнениям
(3.16) - (3.18) соответствует структурная
схема, показанная на рис. 3.11. Она
идентична структурной схеме двигателя
постоянного тока, но имеет другие
коэффициенты.
равнениям
(3.16) - (3.18) соответствует структурная
схема, показанная на рис. 3.11. Она
идентична структурной схеме двигателя
постоянного тока, но имеет другие
коэффициенты.
Таким образом, при определенных допущениях любая электромеханическая система с асинхронным двигателем может быть представлена некоторой эквивалентной системой с двигателем постоянного тока. Но при этом необходимо помнить, что данная упрощенная структура с двигателем переменного тока будет с достаточной для инженерных расчетов точностью справедлива только в режиме малых отклонений переменных от значений установившегося режима и при моменте на валу двигателя не более 1,2 номинального момента. Асинхронные двигатели как элементы систем автоматики рассматриваются в / 7/.
